21.2 第7课时 求二次函数的关系式课件(22张PPT)
文档属性
| 名称 | 21.2 第7课时 求二次函数的关系式课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 457.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-15 00:00:00 | ||
图片预览







文档简介
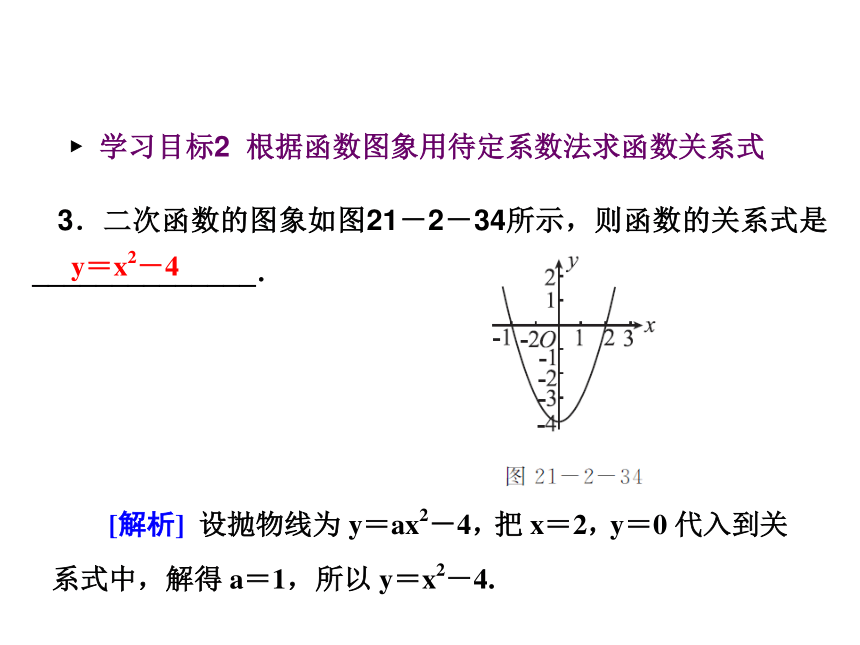
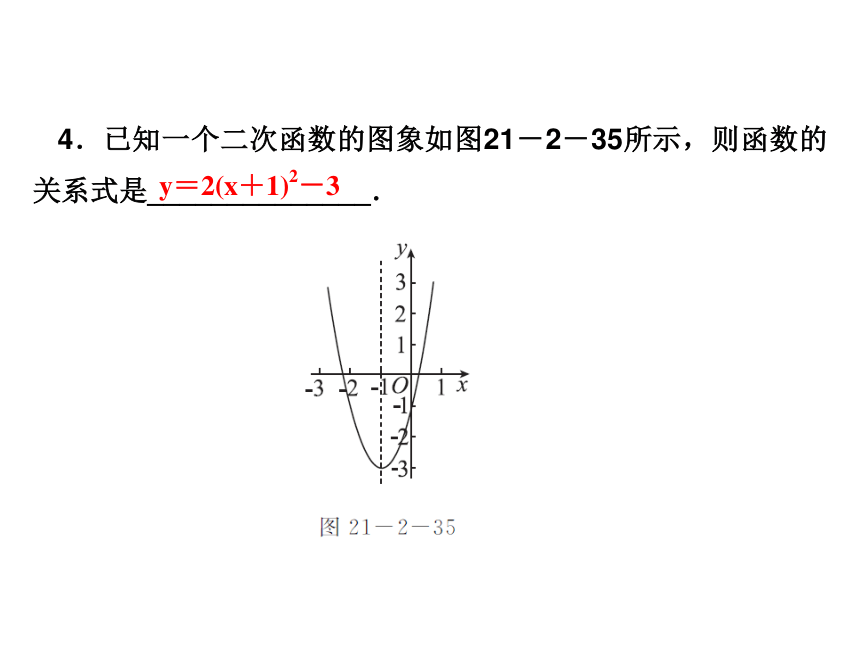
课件22张PPT。数 学新课标(HK) 九年级上册第21章 二次函数与反比例函数21.2 二次函数的图象和性质第7课时 求二次函数的关系式基础自主学习 ? 学习目标1 会用待定系数法求函数关系式第7课时 求二次函数的关系式[归纳] 用待定系数法求函数关系式,关键是正确将点的坐标代入关系式中.第7课时 求二次函数的关系式 ? 学习目标2 根据函数图象用待定系数法求函数关系式3.二次函数的图象如图21-2-34所示,则函数的关系式是______________.第7课时 求二次函数的关系式4.已知一个二次函数的图象如图21-2-35所示,则函数的关系式是______________.第7课时 求二次函数的关系式[归纳] 根据函数图象设函数关系式是关键,如果已知顶点,设顶点式较为简便.重难互动探究第7课时 求二次函数的关系式探究问题一 待定系数法求函数关系式 第7课时 求二次函数的关系式第7课时 求二次函数的关系式[归纳总结] 用待定系数法求函数关系式,关键是根据所给条件设出相应的关系式,如果已知三点设一般式,如果已知顶点和另一点设顶点式,如果已知抛物线和x轴交点就设交点式. 第7课时 求二次函数的关系式[解析] 根据表中自变量和函数对应关系,选择对应值代入到函数关系式中,利用待定系数法求函数关系式. 第7课时 求二次函数的关系式[归纳总结] 将点的坐标代入函数关系式,然后用待定系数法求关系式.探究问题二 关于二次函数与一次函数相交的问题第7课时 求二次函数的关系式第7课时 求二次函数的关系式第7课时 求二次函数的关系式第7课时 求二次函数的关系式[归纳总结] 根据函数图象求函数关系式,一般都要给出图象经过的点的坐标.本题借助于已知的一次函数关系式可以求出一次函数图象与坐标轴的交点,从而获知抛物线与坐标轴的交点,然后代入到函数关系式中即可求出. 第7课时 求二次函数的关系式例4 [教材例题的拓展题] 如图21-2-37,已知抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于点C(0,3).
(1)求抛物线的函数关系式;
(2)求直线BC的函数关系式;
(3)在x轴上方的抛物线上,是否存在一
点P(P点与C点不重合),使△PAB的面
积等于△ABC的面积?若存在,求出
点P的坐标;若不存在,请说明理由.第7课时 求二次函数的关系式第7课时 求二次函数的关系式第7课时 求二次函数的关系式第7课时 求二次函数的关系式[归纳总结] 当两个函数相交时,交点要满足两个函数关系式.一次函数需要两个条件代入求关系式,二次函数需要三个条件代入求关系式.课 堂 小 结第7课时 求二次函数的关系式第7课时 求二次函数的关系式
(1)求抛物线的函数关系式;
(2)求直线BC的函数关系式;
(3)在x轴上方的抛物线上,是否存在一
点P(P点与C点不重合),使△PAB的面
积等于△ABC的面积?若存在,求出
点P的坐标;若不存在,请说明理由.第7课时 求二次函数的关系式第7课时 求二次函数的关系式第7课时 求二次函数的关系式第7课时 求二次函数的关系式[归纳总结] 当两个函数相交时,交点要满足两个函数关系式.一次函数需要两个条件代入求关系式,二次函数需要三个条件代入求关系式.课 堂 小 结第7课时 求二次函数的关系式第7课时 求二次函数的关系式
