21.4 第2课时 建立二次函数的模型解决实际问题课件(27张PPT)
文档属性
| 名称 | 21.4 第2课时 建立二次函数的模型解决实际问题课件(27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 525.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-15 14:42:38 | ||
图片预览






文档简介
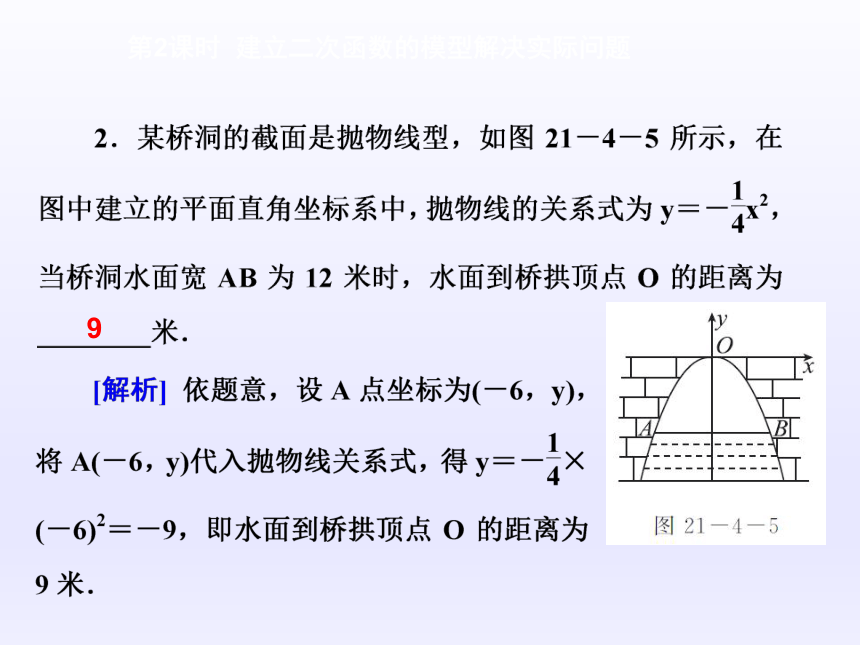
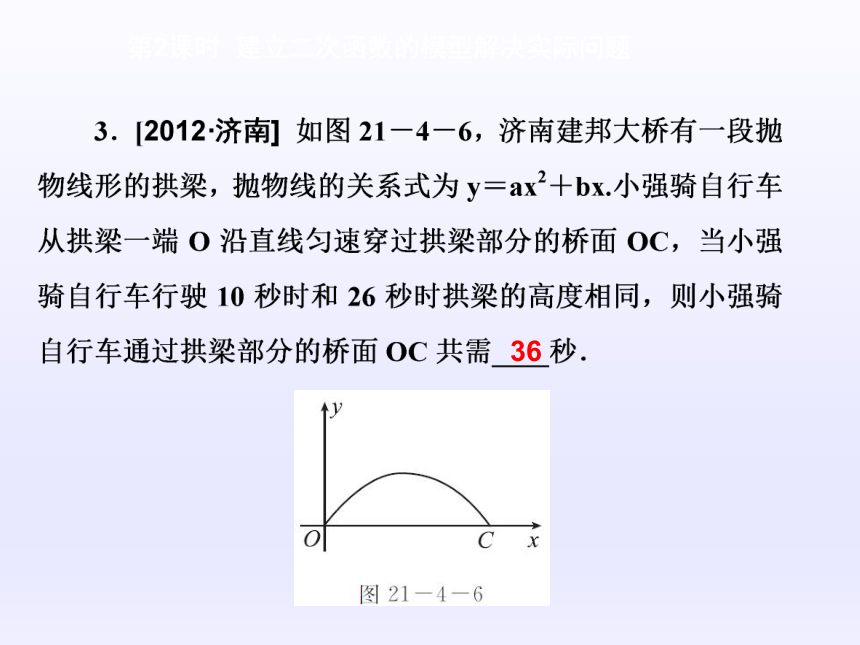
课件27张PPT。数 学新课标(HK) 九年级上册第21章 二次函数与反比例函数21.4 二次函数的应用第2课时 建立二次函数的模型解决实际问题基础自主学习 ? 学习目标1 阅读本课时例题,会根据函数图象利用函数性质解决实际问题 第2课时 建立二次函数的模型解决实际问题A 第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题9 第2课时 建立二次函数的模型解决实际问题36 第2课时 建立二次函数的模型解决实际问题[解析] 设在10秒时到达A点,在26秒时到达B点,桥面OC的最高点为D点,
∵10秒时和26秒时拱梁的高度相同,
∴点A,B关于抛物线的对称轴对称.
∵从A到B需要16秒,∴从A到D需要8秒,
∴从O到D需要10+8=18(秒),
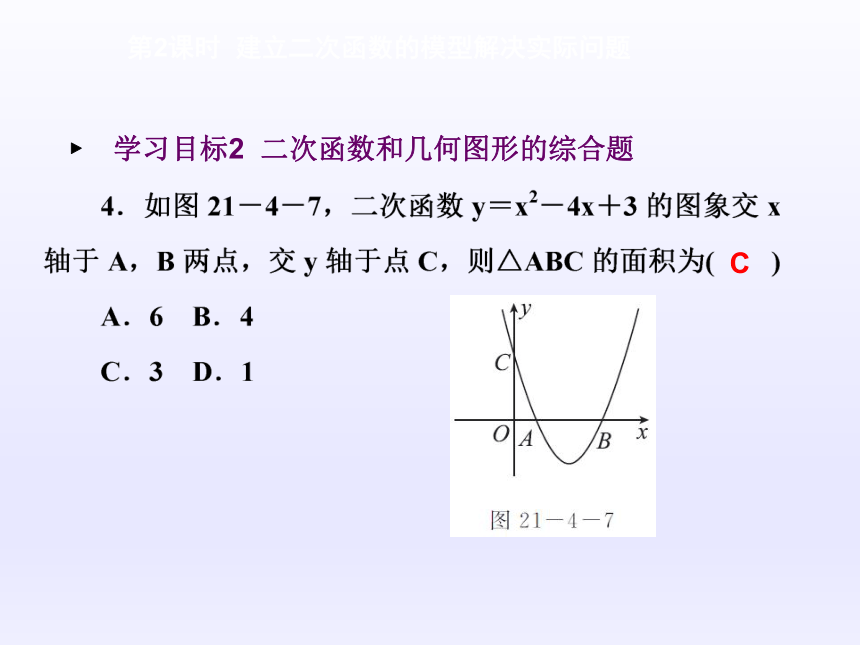
∴从O到C需要2×18=36(秒).[归纳] 根据函数图象确定函数的关系式,然后利用函数的性质解决实际问题. 第2课时 建立二次函数的模型解决实际问题 ? 学习目标2 二次函数和几何图形的综合题 C 第2课时 建立二次函数的模型解决实际问题C [解析] 连接MN,与抛物线交于P点,根据两点之间线段最短得到此时PM+PN最短,设直线MN的关系式为y=kx+b,求出直线MN的关系式,与抛物线关系式联立组成方程组,求出方程组的解得到x与y的值,此时可以得到两组x与y的值,只有位于线段MN上的点,才符合要求,因而由此可确定P点的坐标.第2课时 建立二次函数的模型解决实际问题[归纳] 二次函数常常与几何图形相结合,应学会已知两个点的坐标求线段的长度.常常会考查二次函数图象与坐标轴围成的三角形以及二次函数的对称性在几何中的应用. 重难互动探究第2课时 建立二次函数的模型解决实际问题探究问题一 根据函数图象建立函数模型解决实际问题例1 [教材例题变式题] 某公园草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4 m加设不锈钢做成的立柱(如图21-4-8),试计算所需不锈钢立柱的总长度. 第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题[归纳总结] (1)合理建立平面直角坐标系,可减小计算难度;(2)由相关线段的长写出点的坐标,由点的坐标求出相应线段的长,是解决问题的关键.探究问题二 建立二次函数模型解决实际问题第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题[解析] (1)在所给定的平面直角坐标系中通过描点、连线等步骤画出图形,根据图象判断该函数为二次函数,再将三点坐标代入其中即可求得二次函数的关系式;
(2)根据所求函数关系式,利用配
方求得最大利润.解:(1)画图如图21-4-11所示:第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题[归纳总结] 当两个变量之间的函数关系没有明确给出时,需要通过图象分析属于哪种函数关系,用待定系数法求出函数关系式是关键.探究问题三 二次函数与几何图形的综合题第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题[归纳总结] “点”是否存在问题,点的坐标代入抛物线关系式,有解则点存在,无解则点不存在;本题的解题关键是对角线互相平分的四边形是平行四边形,由此可得点P的纵坐标,继而将点P的纵坐标代入抛物线关系式求得点P的横坐标.课 堂 小 结第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题=3或4 9000 第2课时 建立二次函数的模型解决实际问题[点评] 利用二次函数解决实际问题时,往往会遇到这样的情形:(1)顶点不符合条件,如上问题中x不是正整数,为此,我们要结合二次函数的性质考虑问题中最接近顶点的整数值的情况;(2)顶点不在自变量的取值范围内,这时,我们要结合图象考虑x有意义的区域内的最值情况.
∵10秒时和26秒时拱梁的高度相同,
∴点A,B关于抛物线的对称轴对称.
∵从A到B需要16秒,∴从A到D需要8秒,
∴从O到D需要10+8=18(秒),
∴从O到C需要2×18=36(秒).[归纳] 根据函数图象确定函数的关系式,然后利用函数的性质解决实际问题. 第2课时 建立二次函数的模型解决实际问题 ? 学习目标2 二次函数和几何图形的综合题 C 第2课时 建立二次函数的模型解决实际问题C [解析] 连接MN,与抛物线交于P点,根据两点之间线段最短得到此时PM+PN最短,设直线MN的关系式为y=kx+b,求出直线MN的关系式,与抛物线关系式联立组成方程组,求出方程组的解得到x与y的值,此时可以得到两组x与y的值,只有位于线段MN上的点,才符合要求,因而由此可确定P点的坐标.第2课时 建立二次函数的模型解决实际问题[归纳] 二次函数常常与几何图形相结合,应学会已知两个点的坐标求线段的长度.常常会考查二次函数图象与坐标轴围成的三角形以及二次函数的对称性在几何中的应用. 重难互动探究第2课时 建立二次函数的模型解决实际问题探究问题一 根据函数图象建立函数模型解决实际问题例1 [教材例题变式题] 某公园草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4 m加设不锈钢做成的立柱(如图21-4-8),试计算所需不锈钢立柱的总长度. 第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题[归纳总结] (1)合理建立平面直角坐标系,可减小计算难度;(2)由相关线段的长写出点的坐标,由点的坐标求出相应线段的长,是解决问题的关键.探究问题二 建立二次函数模型解决实际问题第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题[解析] (1)在所给定的平面直角坐标系中通过描点、连线等步骤画出图形,根据图象判断该函数为二次函数,再将三点坐标代入其中即可求得二次函数的关系式;
(2)根据所求函数关系式,利用配
方求得最大利润.解:(1)画图如图21-4-11所示:第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题[归纳总结] 当两个变量之间的函数关系没有明确给出时,需要通过图象分析属于哪种函数关系,用待定系数法求出函数关系式是关键.探究问题三 二次函数与几何图形的综合题第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题[归纳总结] “点”是否存在问题,点的坐标代入抛物线关系式,有解则点存在,无解则点不存在;本题的解题关键是对角线互相平分的四边形是平行四边形,由此可得点P的纵坐标,继而将点P的纵坐标代入抛物线关系式求得点P的横坐标.课 堂 小 结第2课时 建立二次函数的模型解决实际问题第2课时 建立二次函数的模型解决实际问题=3或4 9000 第2课时 建立二次函数的模型解决实际问题[点评] 利用二次函数解决实际问题时,往往会遇到这样的情形:(1)顶点不符合条件,如上问题中x不是正整数,为此,我们要结合二次函数的性质考虑问题中最接近顶点的整数值的情况;(2)顶点不在自变量的取值范围内,这时,我们要结合图象考虑x有意义的区域内的最值情况.
