14.21.5第3课时反比例函数的应用课件
文档属性
| 名称 | 14.21.5第3课时反比例函数的应用课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 508.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-15 00:00:00 | ||
图片预览






文档简介
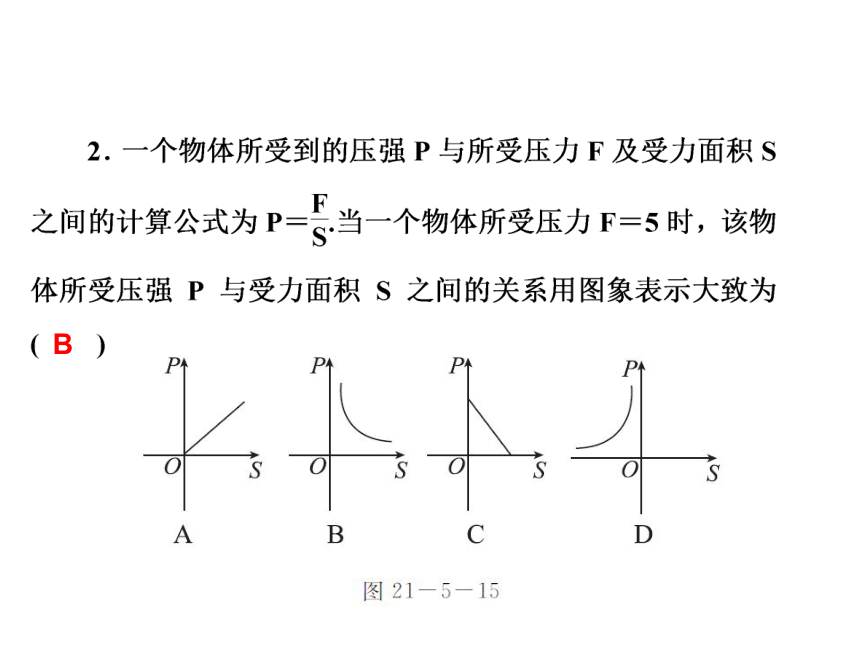
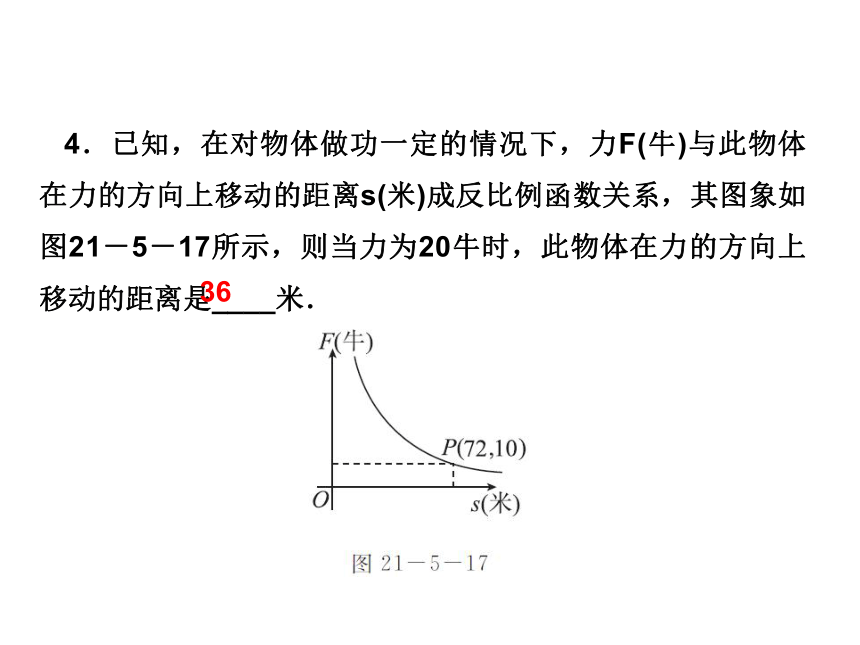
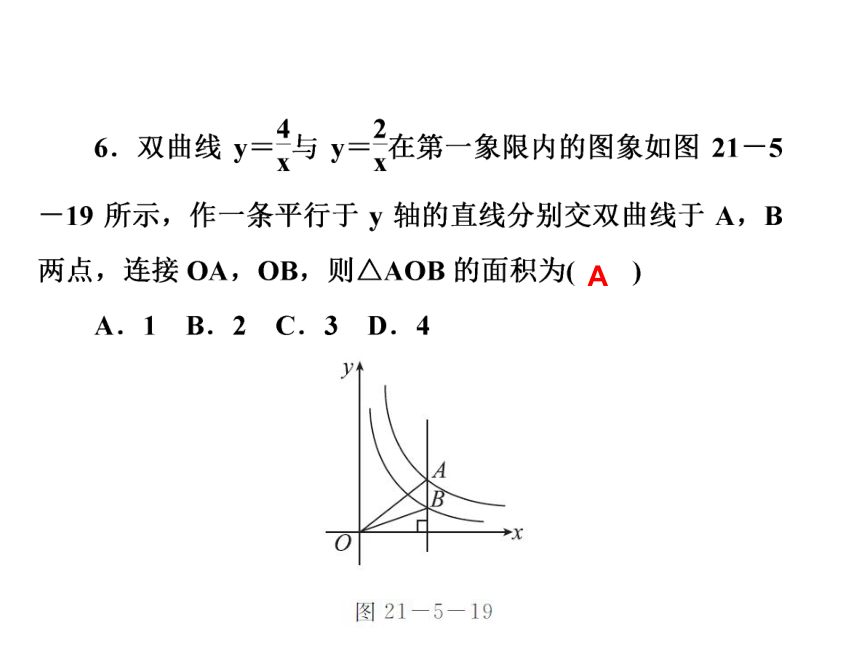
课件25张PPT。数 学新课标(HK) 九年级上册第21章 二次函数与反比例函数21.5 反比例函数第3课时 反比例函数的应用基础自主学习 ? 学习目标1 反比例函数的应用 第3课时 反比例函数的应用B 第3课时 反比例函数的应用B 第3课时 反比例函数的应用3.某种蓄电池的电压为定值,使用此电源时,电流I(A)与可变电阻R(Ω)之间的函数关系如图21-5-16所示,当用电器的电流为10 A时,用电器的可变电阻为____Ω.3.6第3课时 反比例函数的应用4.已知,在对物体做功一定的情况下,力F(牛)与此物体在力的方向上移动的距离s(米)成反比例函数关系,其图象如图21-5-17所示,则当力为20牛时,此物体在力的方向上移动的距离是____米.36第3课时 反比例函数的应用[归纳] 反比例函数和其他函数一样,在我们的日常生活中有着广泛的应用.利用反比例函数的关系解决实际问题,其关键是能够正确地探索两个变量之间的关系.探索两个变量之间的关系和列方程解应用题一样,即弄清题意和题目中的数量关系,找到能够表示应用题全部含义的一个相等关系,根据这个相等的数量关系,列出所需的代数式,从而列出两个变量之间的关系式. 第3课时 反比例函数的应用 ? 学习目标2 理解反比例函数k的几何意义 B 第3课时 反比例函数的应用A 第3课时 反比例函数的应用6 第3课时 反比例函数的应用[归纳] 过反比例函数图象上任意一点P向两个坐标轴作垂线,两条垂线和坐标轴所围成的矩形面积S=|k|.重难互动探究第3课时 反比例函数的应用探究问题一 反比例函数的应用 例1 [教材例题拓展题] 病人按规定的剂量服用某种药物.测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克.已知服药后,2小时前每毫升血液中的含药量y(毫克)与时间x(小时)成正比例.2小时后y与x成反比例(如图21-5-21所示).根据以上信息解答下列问题:
(1)求当0≤x≤2时,y与x的函数关系式;
(2)求当x>2时,y与x的函数关系式;
(3)若每毫升血液中的含药量不低于2毫克时
治疗有效,则服药一次,治疗疾病的有效时间是多长?第3课时 反比例函数的应用第3课时 反比例函数的应用[归纳总结] 根据图象求出函数的关系式,然后再利用反比例函数的性质将实际问题转化为求点的坐标. 探究问题二 反比例函数与一次函数的综合题 第3课时 反比例函数的应用第3课时 反比例函数的应用[解析] (1)将点A的坐标代入一次函数关系式求出m的值,再将A点坐标代入反比例函数关系式中求出k的值.
(2)利用函数图象比较两个函数值的大小.第3课时 反比例函数的应用[归纳总结] 结合函数图象比较函数值大小时,通常找到两函数值相等的点(两函数图象的交点).函数图象的交点以及y轴是两函数值大小变化的分水岭.探究问题三 反比例函数与几何图形的综合题第3课时 反比例函数的应用第3课时 反比例函数的应用第3课时 反比例函数的应用(1)直接判断并填写:不论α取何值,四边形ABCD的形状一定是________.
(2)①当点B为(p,1)时,四边形ABCD是矩形,试求p和m的值;
②观察猜想:对①中的m值,能使四边形ABCD为矩形的点B共有几个?(不必说理)
(3)试探究:四边形ABCD能不能是菱形?若能, 直接写出B点的坐标;若不能, 说明理由.第3课时 反比例函数的应用第3课时 反比例函数的应用第3课时 反比例函数的应用[归纳总结] 利用几何图形的性质,将线段转化为函数图象上点的坐标,从而确定函数的关系式,然后根据函数的性质解答.课 堂 小 结第3课时 反比例函数的应用第3课时 反比例函数的应用
(1)求当0≤x≤2时,y与x的函数关系式;
(2)求当x>2时,y与x的函数关系式;
(3)若每毫升血液中的含药量不低于2毫克时
治疗有效,则服药一次,治疗疾病的有效时间是多长?第3课时 反比例函数的应用第3课时 反比例函数的应用[归纳总结] 根据图象求出函数的关系式,然后再利用反比例函数的性质将实际问题转化为求点的坐标. 探究问题二 反比例函数与一次函数的综合题 第3课时 反比例函数的应用第3课时 反比例函数的应用[解析] (1)将点A的坐标代入一次函数关系式求出m的值,再将A点坐标代入反比例函数关系式中求出k的值.
(2)利用函数图象比较两个函数值的大小.第3课时 反比例函数的应用[归纳总结] 结合函数图象比较函数值大小时,通常找到两函数值相等的点(两函数图象的交点).函数图象的交点以及y轴是两函数值大小变化的分水岭.探究问题三 反比例函数与几何图形的综合题第3课时 反比例函数的应用第3课时 反比例函数的应用第3课时 反比例函数的应用(1)直接判断并填写:不论α取何值,四边形ABCD的形状一定是________.
(2)①当点B为(p,1)时,四边形ABCD是矩形,试求p和m的值;
②观察猜想:对①中的m值,能使四边形ABCD为矩形的点B共有几个?(不必说理)
(3)试探究:四边形ABCD能不能是菱形?若能, 直接写出B点的坐标;若不能, 说明理由.第3课时 反比例函数的应用第3课时 反比例函数的应用第3课时 反比例函数的应用[归纳总结] 利用几何图形的性质,将线段转化为函数图象上点的坐标,从而确定函数的关系式,然后根据函数的性质解答.课 堂 小 结第3课时 反比例函数的应用第3课时 反比例函数的应用
