21.2.2 二次函数y=ax2+k图象和性质(第一课时)
文档属性
| 名称 | 21.2.2 二次函数y=ax2+k图象和性质(第一课时) |
|
|
| 格式 | zip | ||
| 文件大小 | 680.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-16 00:00:00 | ||
图片预览

文档简介
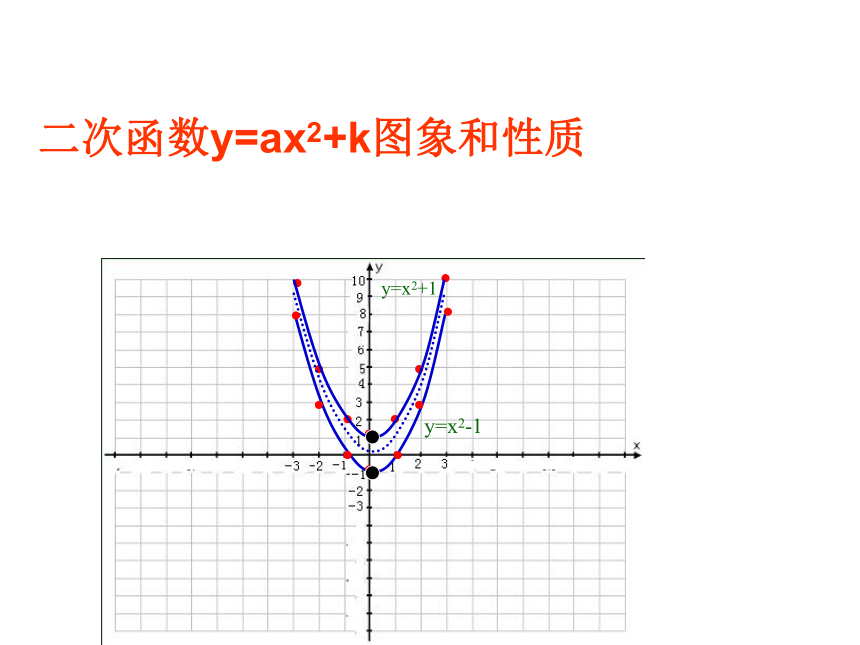
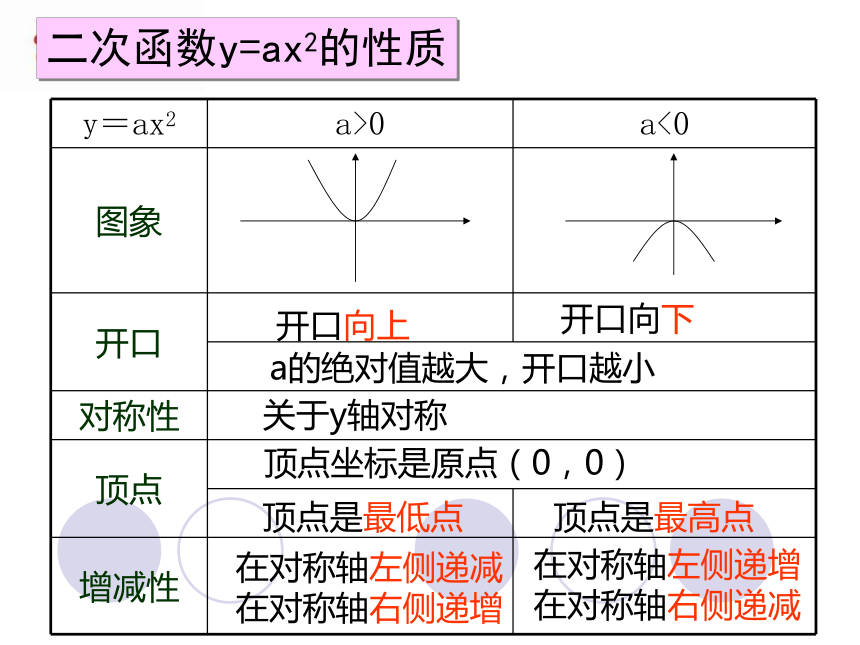
课件33张PPT。二次函数y=ax2+k图象和性质y=x2-1y=x2+1二次函数y=ax2的性质开口向上
开口向下
a的绝对值越大,开口越小
关于y轴对称顶点坐标是原点(0,0)
顶点是最低点顶点是最高点在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
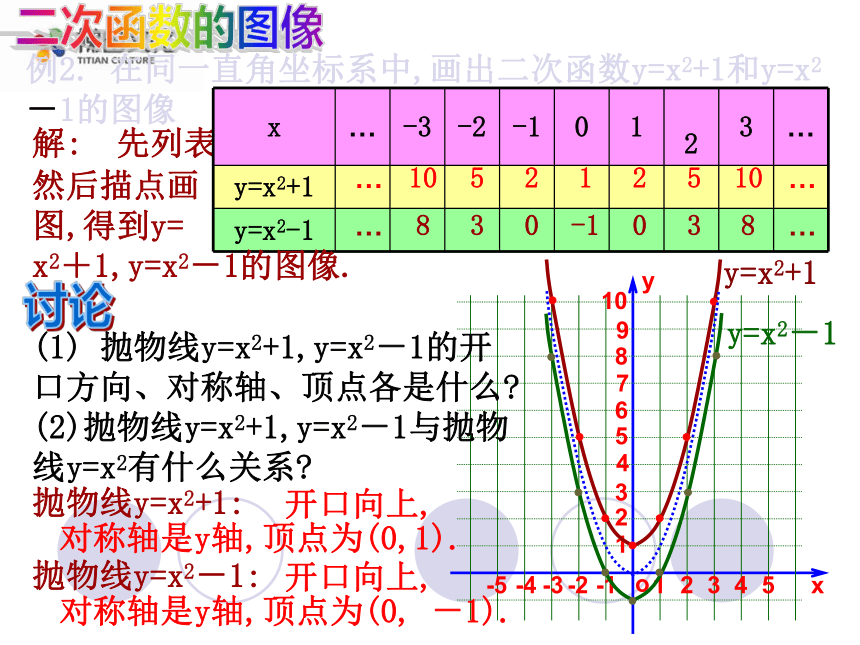
二次函数的图像例2. 在同一直角坐标系中,画出二次函数y=x2+1和y=x2 -1的图像解: 先列表然后描点画 图,得到y= x2+1,y=x2-1的图像.(1) 抛物线y=x2+1,y=x2-1的开口方向、对称轴、顶点各是什么?
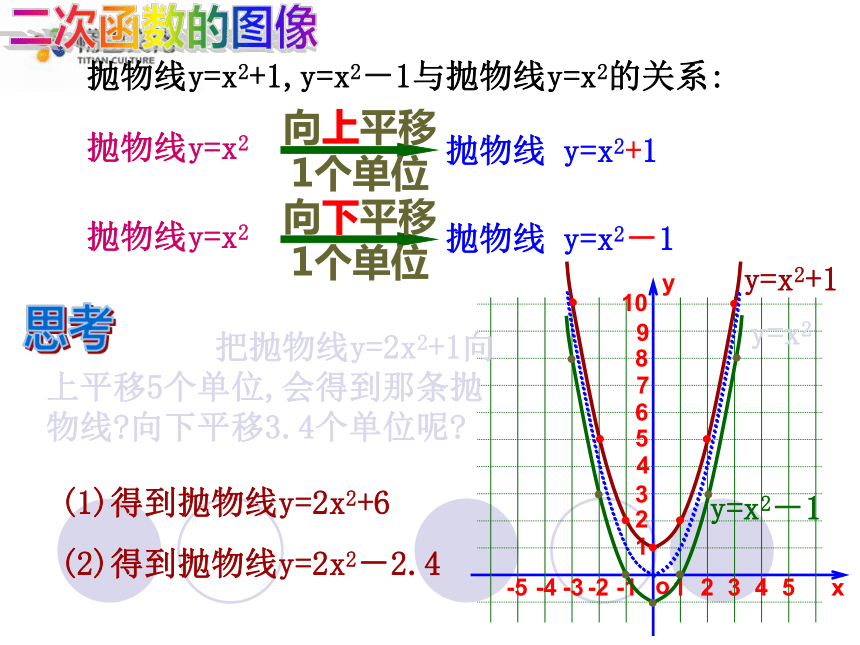
(2)抛物线y=x2+1,y=x2-1与抛物线y=x2有什么关系?讨论抛物线y=x2+1:开口向上,顶点为(0,1).对称轴是y轴,抛物线y=x2-1:开口向上,顶点为(0, -1).对称轴是y轴,y=x2+1y=x2-1二次函数的图像抛物线y=x2+1,y=x2-1与抛物线y=x2的关系:y=x2+1抛物线y=x2抛物线 y=x2-1向上平移
1个单位 把抛物线y=2x2+1向上平移5个单位,会得到那条抛物线?向下平移3.4个单位呢?抛物线y=x2向下平移
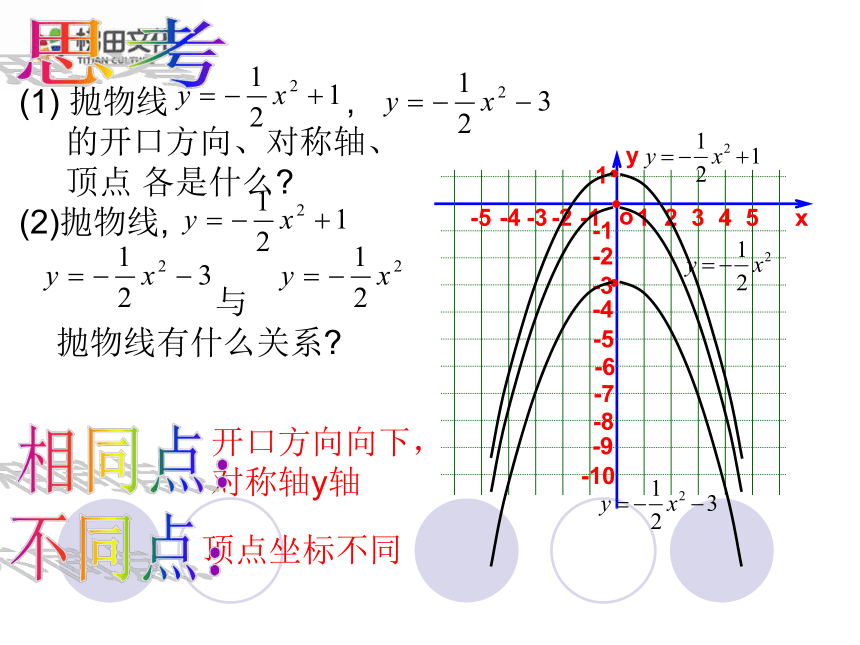
1个单位思考(1)得到抛物线y=2x2+6(2)得到抛物线y=2x2-2.4y=x2-1y=x2抛物线 y=x2+1(1) 抛物线 ,
的开口方向、对称轴、
顶点 各是什么?
(2)抛物线,
与
抛物线有什么关系? 开口方向向下,
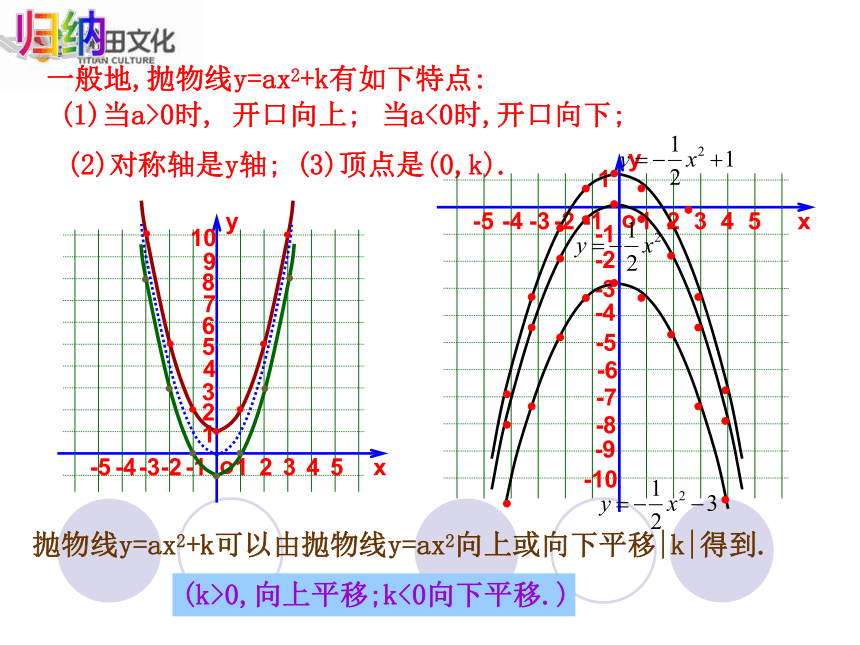
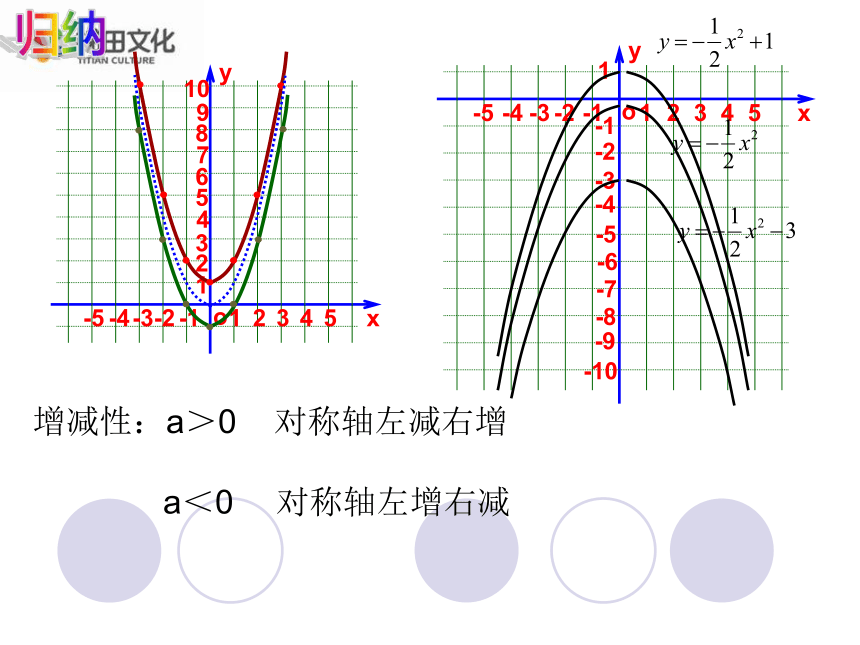
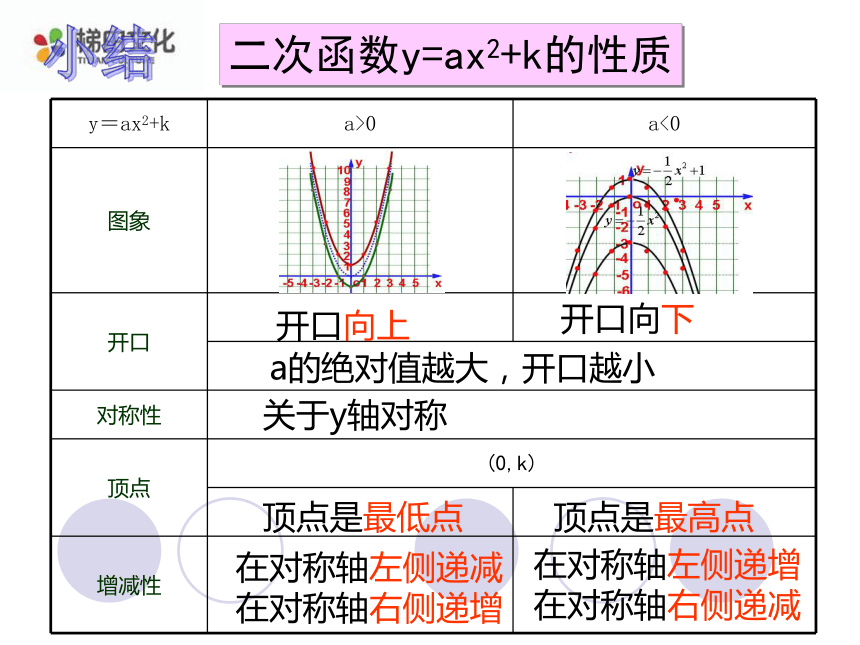
对称轴y轴顶点坐标不同思考不同点:相同点:归纳一般地,抛物线y=ax2+k有如下特点:(1)当a>0时, 开口向上;当a<0时,开口向下;(2)对称轴是y轴;(3)顶点是(0,k).抛物线y=ax2+k可以由抛物线y=ax2向上或向下平移|k|得到.(k>0,向上平移;k<0向下平移.)归纳增减性:a>0 对称轴左减右增
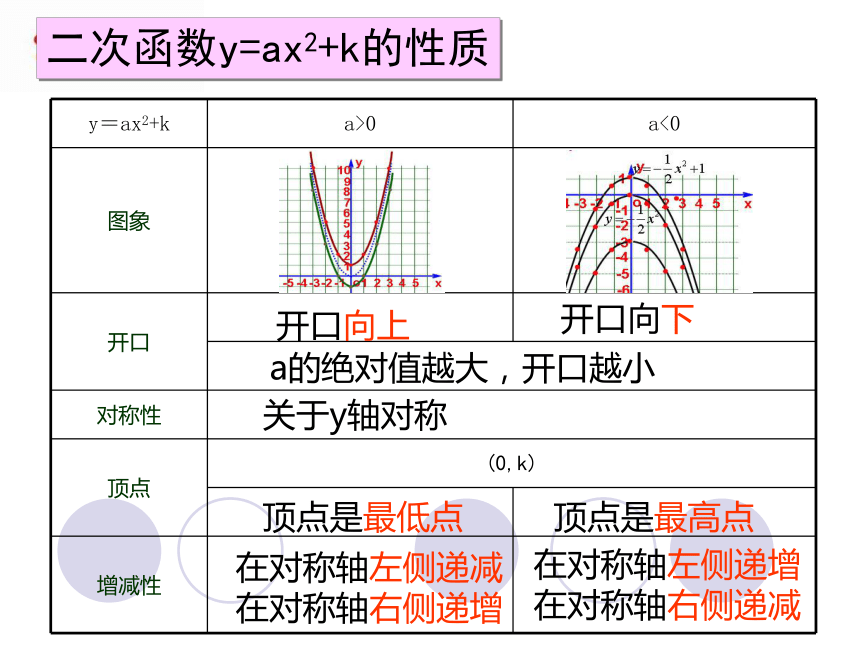
a<0 对称轴左增右减二次函数y=ax2+k的性质开口向上
开口向下
a的绝对值越大,开口越小
关于y轴对称顶点是最低点顶点是最高点在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
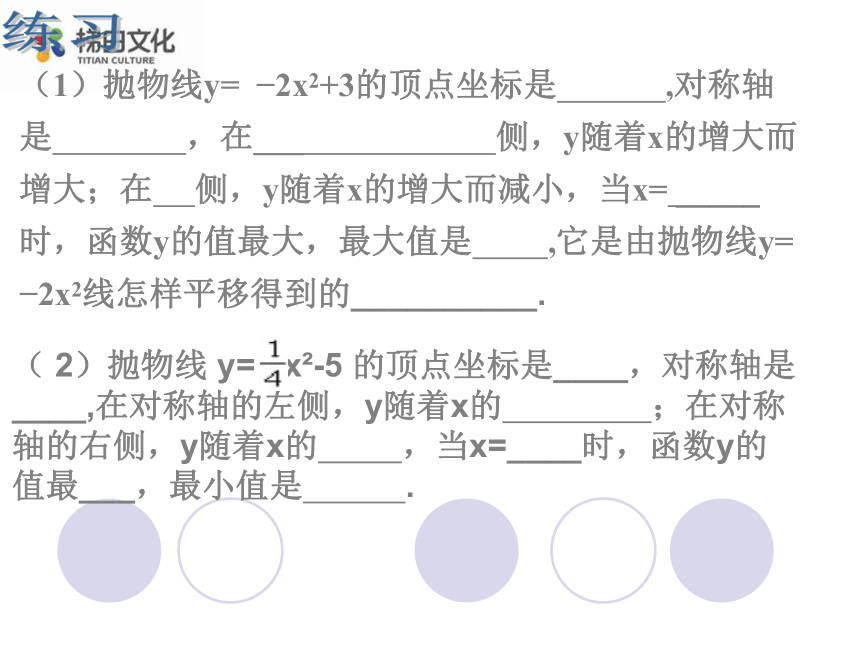
(1)抛物线y= ?2x2+3的顶点坐标是 ,对称轴是 ,在___ 侧,y随着x的增大而增大;在 侧,y随着x的增大而减小,当x= _____ 时,函数y的值最大,最大值是 ,它是由抛物线y= ?2x2线怎样平移得到的__________.练习( 2)抛物线 y= x2-5 的顶点坐标是____,对称轴是____,在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的 ,当x=____时,函数y的值最___,最小值是 .1、按下列要求求出二次函数的解析式:
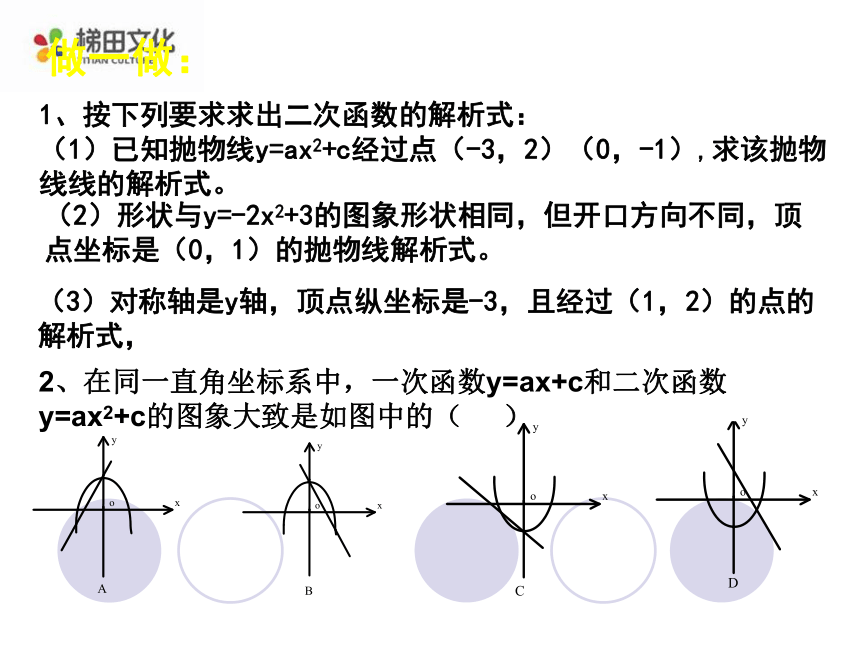
(1)已知抛物线y=ax2+c经过点(-3,2)(0,-1),求该抛物线线的解析式。(2)形状与y=-2x2+3的图象形状相同,但开口方向不同,顶点坐标是(0,1)的抛物线解析式。(3)对称轴是y轴,顶点纵坐标是-3,且经过(1,2)的点的解析式,做一做:2、在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致是如图中的( )二次函数y=ax2+k的性质开口向上
开口向下
a的绝对值越大,开口越小
关于y轴对称顶点是最低点顶点是最高点在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
小结再见例:画出函数 的图像xy=-1/2(x+1)2..................0 -3 -2-12 3 1y=-1/2(x-1)2-2-0.50-0.5-2-4.5-4.5-2-0.50-0.5-2x= -1x=1想一想:三条抛物线
有什么关系?答:形状相同,位置不同。
三个图象之间通过沿x轴平
移可重合。小 结向上向上向下向下Y轴X = -hY轴X = h(0,0)(h,0)(0,0)(-h,0)26.二次函数y=a (x+m)2+k的图像y=ax2y=a(x-h)2y=ax2+cy=ax2c>0c<0上移下移左 加右 减说出平移方式,并指出其顶点与对称轴。1.把二次函数y =6(x+3)2的图像,沿y 轴向下平移2个单位,向左平移3个单位,得到____________的图像.
2.把二次函数_____________的图像,沿x 轴向右平移2个单位,沿y 轴向下平移3个单位,得到y =6(x-3)2+5的图像.
3.把二次函数y =6(x-3)2+5的图像,沿x 轴_______平移______个单位,再沿y 轴向______平移_______个单位,图像过原点.自测:例题例3.画出函数 的图像.指出它的开口方向、顶点与对称轴、解: 列表描点、连线-5.5-3-1.5-1-1.5-3-5.5直线x=-1抛物线
的开口方向、对称轴、顶点?抛物线
的开口向下,对称轴是直线x=-1,顶点是(-1, -1).向左平移1个单位向下平移1个单位向左平移1个单位向下平移1个单位平移方法1:平移方法2:二次函数图像平移x=-1(2)抛物线 与 有什么关系? 归纳 一般地,抛物线y=a(x-h)2+k与y=ax2形状相同,位置不同.把抛物线y=ax2向上(下)向右(左)平移,可以得到抛物线y=a(x -h)2+k.平移的方向、距离要根据h、k的值来决定.向左(右)平移|h|个单位向上(下)平移|k|个单位y=ax2y=a(x-h)2y=a(x-h)2+ky=ax2y=a(x-h)2+k向上(下)平移|k|个单位y=ax2+k向左(右)平移|h|个单位平移方法:抛物线y=a(x-h)2+k有如下特点: (1)当a>0时, 开口向上;当a<0时,开口向上;(2)对称轴是直线x=h;(3)顶点是(h,k).练习向上(1,-2)向下向下(3,7)(2,-6)向上直线x=-3直线x=1直线x=3直线x=2(-3,5)y=-3(x-1)2-2y = 4(x-3)2+7y=-5(2-x)2-61.完成下列表格:2.请回答抛物线y = 4(x-3)2+7由抛物线y=4x2怎样平移得到?3.抛物线y =-4(x-3)2+7能够由抛物线y=4x2平移得到吗?y = ax2y = ax2 + k y = a(x - h )2y = a( x - h )2 + k上下平移左右平移上下平移左右平移结论: 抛物线 y = a(x-h)2+k与y = ax2形状相同,位置不同。各种形式的二次函数的关系如何平移:一个运动员推铅球,铅球出手点在A处,出手时球离地面 m ,铅球运行所经过的路线是抛物,已知铅球在运动员前4m处达到最高点,最高点高为3m,你能算出该运动员的成绩吗?4米3米一场篮球赛中,小明跳起投篮,已知球出手时离地面高 米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行的轨迹为抛物线,篮圈中心距离地面3米。问此球能否投中?3米8米4米4米(4,4)(8,3)在出手角度和力度都不变的情况下,小明的出手高度为多少时能将篮球投入篮圈?0 1 2 3 4 5 6 7 8 9(8,3)(5,4)(4,4)0 1 2 3 4 5 6 7 8 9在出手角度、力度及高度都不变的情况下,则小明朝着篮球架再向前平移多少米后跳起投篮也能将篮球投入篮圈?(7,3)●练习y= ?2(x+3)2-2画出下列函数图象,并说出抛物线的开口方向、对称轴、顶点,最大值或最小值各是什么及增减性如何?y= 2(x-3)2+3y= ?2(x-2)2-1y= 3(x+1)2+1练习1在平面直角坐标系xoy中画出
二次函数y= (x-6)2+3的图像;
此图象与x轴、y轴交点坐标各是多少?
根据图像,说出x取哪些值,函数值y=0?y〉0?y〈0?例题2已知抛物线 ,将这条抛物线平移,当它的顶点移到点M(2,4)的位置时,所得新抛物线的表达式是什么? 练习2 与二次函数y=2(x+3)2-1的图像形状相同,方向相反,且过点(-2,0),(-3,-10)的是函数_____________的图像. 例3抛物线y=-x2+mx-n的对称轴为x=-3,且过点(0,4)求m、n的值.
练习3
抛物线 向上平移2个单位,再向左平移4个单位,得到抛物线 ,求b、c的值. 拓展:求解析式1、已知二次函数的图像的对称轴是直线x=4,在y轴上的截距为6,且过点(2,0)求它的解析式。
2、在同一直角坐标系中,二次函数y=ax2+bx+c的图像与一次函数y=kx+m的图像交于点(3,13),若一次函数的图像在y轴上截距是1,当x=1时二次函数的最小值是5,求这两个函数的解析式。3、已知二次函数的图像经过点(1,9)和(2,4)且它与x轴只有一个交点,求这个二次函数。
4、如图所示的抛物线是把y=-x2经过平移而得到的,这时抛物线经过原点O和X轴正方向上一点A,顶点为P,当∠OPA=90°时,求抛物线的顶点P的坐标及解析式5、已知A为抛物线
的顶 点,B为抛物线与y轴的交点。C为X轴上一点,设线段BC,AC,AB的长度分别为a,b,c当a+c=2b时求经过B、C两点直线的解析式。例题C(3,0)B(1,3) 例4.要修建一个圆形喷水池,在池中心竖直安装一根水管.在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?A解:如图建立直角坐标系, 点(1,3)是图中这段抛物线的顶点. 因此可设这段抛物线对应的函数是∵这段抛物线经过点(3,0)∴ 0=a(3-1)2+3解得:因此抛物线的解析式为:y=a(x-1)2+3 (0≤x≤3)当x=0时,y=2.25答:水管长应为2.25m.
开口向下
a的绝对值越大,开口越小
关于y轴对称顶点坐标是原点(0,0)
顶点是最低点顶点是最高点在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
二次函数的图像例2. 在同一直角坐标系中,画出二次函数y=x2+1和y=x2 -1的图像解: 先列表然后描点画 图,得到y= x2+1,y=x2-1的图像.(1) 抛物线y=x2+1,y=x2-1的开口方向、对称轴、顶点各是什么?
(2)抛物线y=x2+1,y=x2-1与抛物线y=x2有什么关系?讨论抛物线y=x2+1:开口向上,顶点为(0,1).对称轴是y轴,抛物线y=x2-1:开口向上,顶点为(0, -1).对称轴是y轴,y=x2+1y=x2-1二次函数的图像抛物线y=x2+1,y=x2-1与抛物线y=x2的关系:y=x2+1抛物线y=x2抛物线 y=x2-1向上平移
1个单位 把抛物线y=2x2+1向上平移5个单位,会得到那条抛物线?向下平移3.4个单位呢?抛物线y=x2向下平移
1个单位思考(1)得到抛物线y=2x2+6(2)得到抛物线y=2x2-2.4y=x2-1y=x2抛物线 y=x2+1(1) 抛物线 ,
的开口方向、对称轴、
顶点 各是什么?
(2)抛物线,
与
抛物线有什么关系? 开口方向向下,
对称轴y轴顶点坐标不同思考不同点:相同点:归纳一般地,抛物线y=ax2+k有如下特点:(1)当a>0时, 开口向上;当a<0时,开口向下;(2)对称轴是y轴;(3)顶点是(0,k).抛物线y=ax2+k可以由抛物线y=ax2向上或向下平移|k|得到.(k>0,向上平移;k<0向下平移.)归纳增减性:a>0 对称轴左减右增
a<0 对称轴左增右减二次函数y=ax2+k的性质开口向上
开口向下
a的绝对值越大,开口越小
关于y轴对称顶点是最低点顶点是最高点在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
(1)抛物线y= ?2x2+3的顶点坐标是 ,对称轴是 ,在___ 侧,y随着x的增大而增大;在 侧,y随着x的增大而减小,当x= _____ 时,函数y的值最大,最大值是 ,它是由抛物线y= ?2x2线怎样平移得到的__________.练习( 2)抛物线 y= x2-5 的顶点坐标是____,对称轴是____,在对称轴的左侧,y随着x的 ;在对称轴的右侧,y随着x的 ,当x=____时,函数y的值最___,最小值是 .1、按下列要求求出二次函数的解析式:
(1)已知抛物线y=ax2+c经过点(-3,2)(0,-1),求该抛物线线的解析式。(2)形状与y=-2x2+3的图象形状相同,但开口方向不同,顶点坐标是(0,1)的抛物线解析式。(3)对称轴是y轴,顶点纵坐标是-3,且经过(1,2)的点的解析式,做一做:2、在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致是如图中的( )二次函数y=ax2+k的性质开口向上
开口向下
a的绝对值越大,开口越小
关于y轴对称顶点是最低点顶点是最高点在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
小结再见例:画出函数 的图像xy=-1/2(x+1)2..................0 -3 -2-12 3 1y=-1/2(x-1)2-2-0.50-0.5-2-4.5-4.5-2-0.50-0.5-2x= -1x=1想一想:三条抛物线
有什么关系?答:形状相同,位置不同。
三个图象之间通过沿x轴平
移可重合。小 结向上向上向下向下Y轴X = -hY轴X = h(0,0)(h,0)(0,0)(-h,0)26.二次函数y=a (x+m)2+k的图像y=ax2y=a(x-h)2y=ax2+cy=ax2c>0c<0上移下移左 加右 减说出平移方式,并指出其顶点与对称轴。1.把二次函数y =6(x+3)2的图像,沿y 轴向下平移2个单位,向左平移3个单位,得到____________的图像.
2.把二次函数_____________的图像,沿x 轴向右平移2个单位,沿y 轴向下平移3个单位,得到y =6(x-3)2+5的图像.
3.把二次函数y =6(x-3)2+5的图像,沿x 轴_______平移______个单位,再沿y 轴向______平移_______个单位,图像过原点.自测:例题例3.画出函数 的图像.指出它的开口方向、顶点与对称轴、解: 列表描点、连线-5.5-3-1.5-1-1.5-3-5.5直线x=-1抛物线
的开口方向、对称轴、顶点?抛物线
的开口向下,对称轴是直线x=-1,顶点是(-1, -1).向左平移1个单位向下平移1个单位向左平移1个单位向下平移1个单位平移方法1:平移方法2:二次函数图像平移x=-1(2)抛物线 与 有什么关系? 归纳 一般地,抛物线y=a(x-h)2+k与y=ax2形状相同,位置不同.把抛物线y=ax2向上(下)向右(左)平移,可以得到抛物线y=a(x -h)2+k.平移的方向、距离要根据h、k的值来决定.向左(右)平移|h|个单位向上(下)平移|k|个单位y=ax2y=a(x-h)2y=a(x-h)2+ky=ax2y=a(x-h)2+k向上(下)平移|k|个单位y=ax2+k向左(右)平移|h|个单位平移方法:抛物线y=a(x-h)2+k有如下特点: (1)当a>0时, 开口向上;当a<0时,开口向上;(2)对称轴是直线x=h;(3)顶点是(h,k).练习向上(1,-2)向下向下(3,7)(2,-6)向上直线x=-3直线x=1直线x=3直线x=2(-3,5)y=-3(x-1)2-2y = 4(x-3)2+7y=-5(2-x)2-61.完成下列表格:2.请回答抛物线y = 4(x-3)2+7由抛物线y=4x2怎样平移得到?3.抛物线y =-4(x-3)2+7能够由抛物线y=4x2平移得到吗?y = ax2y = ax2 + k y = a(x - h )2y = a( x - h )2 + k上下平移左右平移上下平移左右平移结论: 抛物线 y = a(x-h)2+k与y = ax2形状相同,位置不同。各种形式的二次函数的关系如何平移:一个运动员推铅球,铅球出手点在A处,出手时球离地面 m ,铅球运行所经过的路线是抛物,已知铅球在运动员前4m处达到最高点,最高点高为3m,你能算出该运动员的成绩吗?4米3米一场篮球赛中,小明跳起投篮,已知球出手时离地面高 米,与篮圈中心的水平距离为8米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行的轨迹为抛物线,篮圈中心距离地面3米。问此球能否投中?3米8米4米4米(4,4)(8,3)在出手角度和力度都不变的情况下,小明的出手高度为多少时能将篮球投入篮圈?0 1 2 3 4 5 6 7 8 9(8,3)(5,4)(4,4)0 1 2 3 4 5 6 7 8 9在出手角度、力度及高度都不变的情况下,则小明朝着篮球架再向前平移多少米后跳起投篮也能将篮球投入篮圈?(7,3)●练习y= ?2(x+3)2-2画出下列函数图象,并说出抛物线的开口方向、对称轴、顶点,最大值或最小值各是什么及增减性如何?y= 2(x-3)2+3y= ?2(x-2)2-1y= 3(x+1)2+1练习1在平面直角坐标系xoy中画出
二次函数y= (x-6)2+3的图像;
此图象与x轴、y轴交点坐标各是多少?
根据图像,说出x取哪些值,函数值y=0?y〉0?y〈0?例题2已知抛物线 ,将这条抛物线平移,当它的顶点移到点M(2,4)的位置时,所得新抛物线的表达式是什么? 练习2 与二次函数y=2(x+3)2-1的图像形状相同,方向相反,且过点(-2,0),(-3,-10)的是函数_____________的图像. 例3抛物线y=-x2+mx-n的对称轴为x=-3,且过点(0,4)求m、n的值.
练习3
抛物线 向上平移2个单位,再向左平移4个单位,得到抛物线 ,求b、c的值. 拓展:求解析式1、已知二次函数的图像的对称轴是直线x=4,在y轴上的截距为6,且过点(2,0)求它的解析式。
2、在同一直角坐标系中,二次函数y=ax2+bx+c的图像与一次函数y=kx+m的图像交于点(3,13),若一次函数的图像在y轴上截距是1,当x=1时二次函数的最小值是5,求这两个函数的解析式。3、已知二次函数的图像经过点(1,9)和(2,4)且它与x轴只有一个交点,求这个二次函数。
4、如图所示的抛物线是把y=-x2经过平移而得到的,这时抛物线经过原点O和X轴正方向上一点A,顶点为P,当∠OPA=90°时,求抛物线的顶点P的坐标及解析式5、已知A为抛物线
的顶 点,B为抛物线与y轴的交点。C为X轴上一点,设线段BC,AC,AB的长度分别为a,b,c当a+c=2b时求经过B、C两点直线的解析式。例题C(3,0)B(1,3) 例4.要修建一个圆形喷水池,在池中心竖直安装一根水管.在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?A解:如图建立直角坐标系, 点(1,3)是图中这段抛物线的顶点. 因此可设这段抛物线对应的函数是∵这段抛物线经过点(3,0)∴ 0=a(3-1)2+3解得:因此抛物线的解析式为:y=a(x-1)2+3 (0≤x≤3)当x=0时,y=2.25答:水管长应为2.25m.
