21.2.3 二次函数的表达式的确定 课件
文档属性
| 名称 | 21.2.3 二次函数的表达式的确定 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 674.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-16 00:00:00 | ||
图片预览








文档简介
课件22张PPT。第二章 二次函数二次函数二次函数的意义
确定二次函数的表达式
用描点法画出二次函数的图象
从图象上认识二次函数的性质
确定二次函数的顶点、开口方向和对称轴
解决简单的实际问题
复习内容定义:一般地,形如y=ax2+bx+c
(a,b,c是常数,a≠ 0)的函数叫做x的
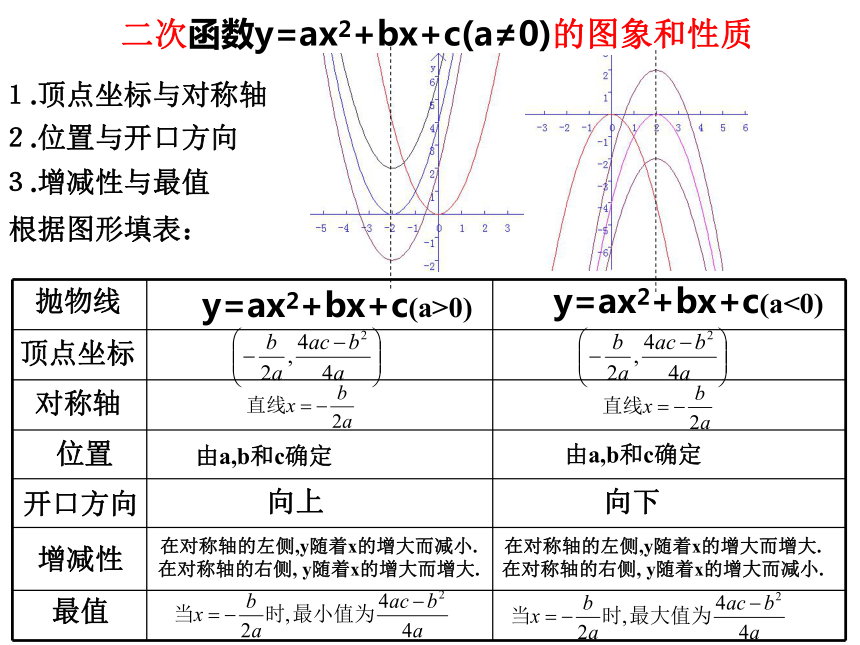
二次函数.二次函数y=a(x-h)2+k的图象和性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=a(x-h)2+k(a>0)y=a(x-h)2+k(a<0)(h,k)(h,k)直线x=h直线x=h由h和k确定由h和k确定向上向下当x=h时,最小值为k.当x=h时,最大值为k.在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 根据图形填表:二次函数y=ax2+bx+c(a≠0)的图象和性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c确定由a,b和c确定向上向下在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 根据图形填表: 二次函数有三种形式如下:
(1)一般式:y=ax2+bx+c(a≠0)
(2)顶点式:y=a(x-h)2+k (a≠0)
(3)两根式:y=a(x-x1)(x-x2) (a≠0)1.已知抛物线y=x2+4x+3它的开口向 ,对
称轴是直线 ,顶点坐标为 ,图
象与x轴的交点为 ,与y轴的交
点为 。练习 上X=-2 (-2,-1) (-3,0),(-1,0) (0,3) (-1,4) 3.写出一个图象经过原点的二次函数的表达式
。评注:图象经过原点的二次函数的表达式是
y=ax2和y=ax2+bx(a≠0)y=x26.已知二次函数y=3(x-1)2+4,当x取哪些值时,y的值随x值的增大而减小?-1典型例题
例1 把一根长100cm的铁丝分成两部分,然后分别围成两个正方形,这两个正方形的面积和最小是多少?
解:设围成的一个正方形边长是xcm,那么另一个
正方形的边长是 cm.根据题意,得
例3 1.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.每件衬衫降价多少元时,商场平均每天盈利最多?
分析:如果每件衬衫降价x元,那么商场平均每天可多售出2x件,则平均每天可售出(20+2x)件,每件盈利(40-x)元.
解:设每件衬衫降价x元,那么商场平均每天可多售出2x件.根据题意,得商场平均每天盈利
y=(20+2x)(40 -x)
=-2x2 +60x+800.
解:设每件衬衫降价x元,那么商场平均每天可多售出 2x件.根据题意,得商场平均每天盈利
y=(20+2x)(40 -x)
=-2x2 +60x+800.
=2. 某商人如果将进货价为8元的商品按每件10元出售,每天可销售100件,现采用提高售出价,减少进货量的办法增加利润,已知这种商品每涨价1元其销售量就要减少10件,问他将售出价定为多少元时,才能使每天所赚的利润最大?并求出最大利润. 例4 某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的200天内,西红柿市场售价 y1(单位:元/100kg)与上市时间x(单位:天)的关系用图3-15的一条线段表示;西红柿的种植成本y2(单位;元/100kg)与上
市时间x(单位:天)的关系是y2= (x-150)2+100.如
图3-16所示.
(1)写出y1与x之间的关系式;
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?
2.某种产品的年产量不超过1000吨,该产品的年产量(单位:吨)与费用(单位:万元)之间函数关系的图象是顶点在原点的抛物线的一部分(如图),产品的年销售量(单位:吨)与单价(单位:万元/吨)之间函数的图象是线段(如图),若生产出的产品都能在当年销售完,那么产量是多少吨时,所获得的毛利润最大?(毛利润=销售额-费用)
如图,在一块三角形区域ABC中,∠C=90°,边AC=8,BC=6,现要在△ABC内建造一个矩形水池DEFG,如图的设计方案是使DE在AB上。
⑴求△ABC中AB边上的高h;
⑵设DG=x,当x取何值时,水池DEFG的面积最大?
有一个拱桥是抛物线形,他的跨度为60,拱高为18,当洪水泛滥时的水面宽度小于30时,要采取紧急措施。若拱顶离水面只有4时,问是否要采取紧急措施?
?
?
? 某校初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高 m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m。
? (1)建立如图的平面直角坐标系,
问此球能否准确投中? (2)此时,若对方队员乙在甲前面
1m处跳起盖帽拦截,
已知乙的最大摸高为3.1m,
那么他能否获得成功?
已知二次函数的图象经过点A(C,-2),
求证:这个二次函数图象的对称轴是x=3.
题目中的矩形框部分是一段被墨水染污了无法辩认的文字.
(1)根据已知和结论中现有的信息,你能否求出题中的二次函数解析式?若能,请写出求解过程,并画出二次函数的图象;若不能,请说明理由.
(2)请你根据已有的信息,在原题中的矩形框中,填加一个适当的条件,把原题补充完整.
我区某镇地理环境偏僻,严重制约经济发展,丰富的花木产品只能在本地销售,我区政府对该花木产品每投资 x万元,所获利润为P=-(x-30)2+10万元.为了响应我国西部大开发的宏伟决策,我区政府在制定经济发展的10年规划时,拟开发此花木产品,而开发前后可用于该项目投资的专项资金每年最多50万元.若开发该产品,在前5年中,必须每年从专项资金中拿出25万元投资修通一条公路,且5年修通.公路修通后,花木产品除在本地销售外,还可运往外地销售,运往外地销售的花木产品,每投资x万元可获利润
Q= - (50-x)2+ (50-x)+308万元.
(1)若不进行开发,求10年所获利润的最大值是多少?
(2)若按此规划进行开发,求10年所获利润的最大值是多少?
(3)根据(1)、(2)计算的结果,请你用一句话谈谈你的想法.
确定二次函数的表达式
用描点法画出二次函数的图象
从图象上认识二次函数的性质
确定二次函数的顶点、开口方向和对称轴
解决简单的实际问题
复习内容定义:一般地,形如y=ax2+bx+c
(a,b,c是常数,a≠ 0)的函数叫做x的
二次函数.二次函数y=a(x-h)2+k的图象和性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=a(x-h)2+k(a>0)y=a(x-h)2+k(a<0)(h,k)(h,k)直线x=h直线x=h由h和k确定由h和k确定向上向下当x=h时,最小值为k.当x=h时,最大值为k.在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 根据图形填表:二次函数y=ax2+bx+c(a≠0)的图象和性质1.顶点坐标与对称轴2.位置与开口方向3.增减性与最值抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c确定由a,b和c确定向上向下在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大. 在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小. 根据图形填表: 二次函数有三种形式如下:
(1)一般式:y=ax2+bx+c(a≠0)
(2)顶点式:y=a(x-h)2+k (a≠0)
(3)两根式:y=a(x-x1)(x-x2) (a≠0)1.已知抛物线y=x2+4x+3它的开口向 ,对
称轴是直线 ,顶点坐标为 ,图
象与x轴的交点为 ,与y轴的交
点为 。练习 上X=-2 (-2,-1) (-3,0),(-1,0) (0,3) (-1,4) 3.写出一个图象经过原点的二次函数的表达式
。评注:图象经过原点的二次函数的表达式是
y=ax2和y=ax2+bx(a≠0)y=x26.已知二次函数y=3(x-1)2+4,当x取哪些值时,y的值随x值的增大而减小?-1典型例题
例1 把一根长100cm的铁丝分成两部分,然后分别围成两个正方形,这两个正方形的面积和最小是多少?
解:设围成的一个正方形边长是xcm,那么另一个
正方形的边长是 cm.根据题意,得
例3 1.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.每件衬衫降价多少元时,商场平均每天盈利最多?
分析:如果每件衬衫降价x元,那么商场平均每天可多售出2x件,则平均每天可售出(20+2x)件,每件盈利(40-x)元.
解:设每件衬衫降价x元,那么商场平均每天可多售出2x件.根据题意,得商场平均每天盈利
y=(20+2x)(40 -x)
=-2x2 +60x+800.
解:设每件衬衫降价x元,那么商场平均每天可多售出 2x件.根据题意,得商场平均每天盈利
y=(20+2x)(40 -x)
=-2x2 +60x+800.
=2. 某商人如果将进货价为8元的商品按每件10元出售,每天可销售100件,现采用提高售出价,减少进货量的办法增加利润,已知这种商品每涨价1元其销售量就要减少10件,问他将售出价定为多少元时,才能使每天所赚的利润最大?并求出最大利润. 例4 某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的200天内,西红柿市场售价 y1(单位:元/100kg)与上市时间x(单位:天)的关系用图3-15的一条线段表示;西红柿的种植成本y2(单位;元/100kg)与上
市时间x(单位:天)的关系是y2= (x-150)2+100.如
图3-16所示.
(1)写出y1与x之间的关系式;
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?
2.某种产品的年产量不超过1000吨,该产品的年产量(单位:吨)与费用(单位:万元)之间函数关系的图象是顶点在原点的抛物线的一部分(如图),产品的年销售量(单位:吨)与单价(单位:万元/吨)之间函数的图象是线段(如图),若生产出的产品都能在当年销售完,那么产量是多少吨时,所获得的毛利润最大?(毛利润=销售额-费用)
如图,在一块三角形区域ABC中,∠C=90°,边AC=8,BC=6,现要在△ABC内建造一个矩形水池DEFG,如图的设计方案是使DE在AB上。
⑴求△ABC中AB边上的高h;
⑵设DG=x,当x取何值时,水池DEFG的面积最大?
有一个拱桥是抛物线形,他的跨度为60,拱高为18,当洪水泛滥时的水面宽度小于30时,要采取紧急措施。若拱顶离水面只有4时,问是否要采取紧急措施?
?
?
? 某校初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面高 m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球运行的轨迹为抛物线,篮圈距地面3m。
? (1)建立如图的平面直角坐标系,
问此球能否准确投中? (2)此时,若对方队员乙在甲前面
1m处跳起盖帽拦截,
已知乙的最大摸高为3.1m,
那么他能否获得成功?
已知二次函数的图象经过点A(C,-2),
求证:这个二次函数图象的对称轴是x=3.
题目中的矩形框部分是一段被墨水染污了无法辩认的文字.
(1)根据已知和结论中现有的信息,你能否求出题中的二次函数解析式?若能,请写出求解过程,并画出二次函数的图象;若不能,请说明理由.
(2)请你根据已有的信息,在原题中的矩形框中,填加一个适当的条件,把原题补充完整.
我区某镇地理环境偏僻,严重制约经济发展,丰富的花木产品只能在本地销售,我区政府对该花木产品每投资 x万元,所获利润为P=-(x-30)2+10万元.为了响应我国西部大开发的宏伟决策,我区政府在制定经济发展的10年规划时,拟开发此花木产品,而开发前后可用于该项目投资的专项资金每年最多50万元.若开发该产品,在前5年中,必须每年从专项资金中拿出25万元投资修通一条公路,且5年修通.公路修通后,花木产品除在本地销售外,还可运往外地销售,运往外地销售的花木产品,每投资x万元可获利润
Q= - (50-x)2+ (50-x)+308万元.
(1)若不进行开发,求10年所获利润的最大值是多少?
(2)若按此规划进行开发,求10年所获利润的最大值是多少?
(3)根据(1)、(2)计算的结果,请你用一句话谈谈你的想法.
