21.3 二次函数与一元二次方程 课件
文档属性
| 名称 | 21.3 二次函数与一元二次方程 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 237.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-16 16:40:25 | ||
图片预览





文档简介
课件17张PPT。二次函数与一元二次方程1.二次函数与一元二次方程的关系
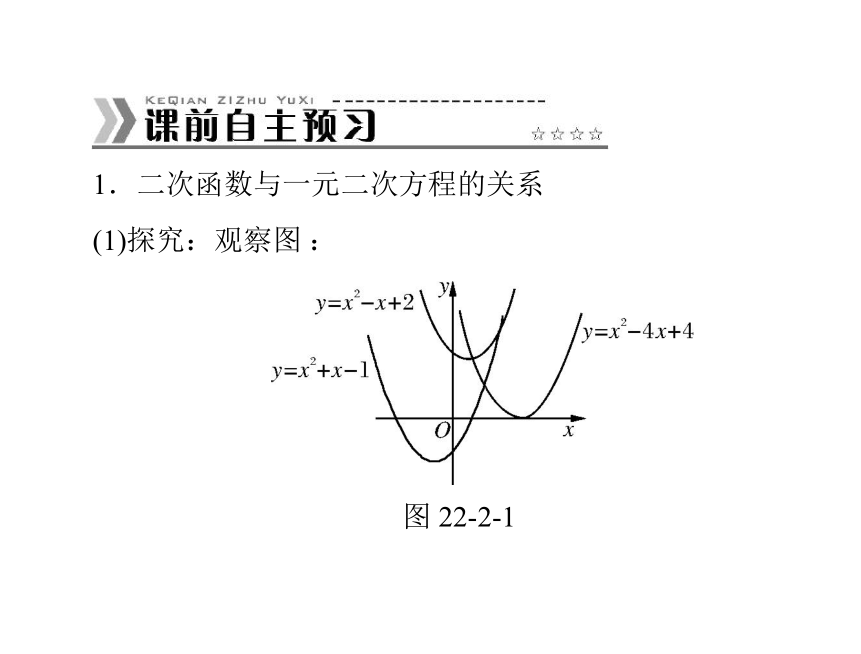
(1)探究:观察图 :图 22-2-1①二次函数 y=x2+x-1 的图象与 x 轴有______个交点,则一元二次方程 x2+x-1=0 的根的判别式Δ______0.2>②二次函数 y=x2-4x+4 的图像与 x 轴有______个交点,则一元二次方程 x2-4x+4=0 的根的判别式Δ______0.1=③二次函数 y=x2-x+2 的图象与 x 轴________公共点,则一元二次方程 x2-x+2=0 的根的判别式Δ______0.无< 归纳:(1)如果抛物线 y=ax2+bx+c 与 x 轴有公共点,公
共点的横坐标是 x0,那么当 x=x0 时,函数的值是____,因此
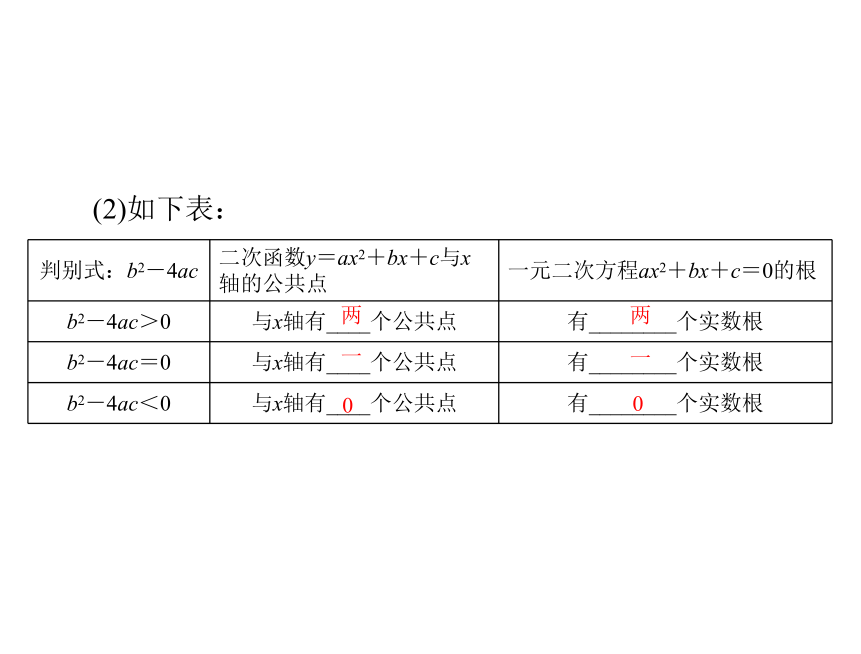
x=x0 就是方程______________的一个根.0ax2+bx+c=0(2)如下表:
两两一一00 2.利用函数图象求一元二次方程的根
步骤:
(1)作函数图象;
(2)确定根所在的________;
(3)通过取________的方法不断缩小根所在的范围,直至符
合题目要求.范围平均数知识点 1二次函数与一元二次方程的关系 【例 1】 已知二次函数 y=mx2-6x+1(m 是常数)的图象与
x 轴只有一个交点,求 m 的值.
思路点拨:“只有一个交点”等价于“方程只有一个根”.
解:当 m=0 时,函数 y=-6x+1 的图象与 x 轴只有一个
交点,当m≠0 时,∵函数 y=mx2-6x+1的图象与 x 轴只有一
个交点,
∴方程 mx2-6x+1=0 有两个相等的实数根.
∴(-6)2-4m=0,解得 m=9.
故 m 的值为 0 或 9.【跟踪训练】C1.函数 y=x2-2x-1 的图象,与 x 轴的交点个数有()A.0 个B.1 个C.2 个D.3 个2.若抛线 y=(a-1)x2+2x+1 与 x 轴只有一个交点,则 a的值为________.2知识点 2利用函数图象求一元二次方程的近似解 【例 2】 利用二次函数的图象,求方程 x2+2x-10=0 的
近似根(精确到 0.1).
思路点拨:先借助二次函数图象确定方程的解的大致范围,
再通过计算进一步精确.
解:作二次函数 y=x2+2x-10 的图象如图 D4,由图象可
知方程 x2+2x-10=0 有两个根,一个在-5 和-4 之间,一个
在 2 和 3 之间.因此两个根分别为-4 点几和 2 点几,下面用
计算器进行探索.因此 x=-4.3 是方程的一个近似根.
另一个根也可以类似地求出:因此 x=2.3 是方程的另一个近似根.图D43.已知 y=x2+2x-10,小明计算器列出了下表:那么 x2+2x-10=0 一个根是()CA.-4.1B.-4.2C.-4.3D.-4.44.如图 22-2-2,(1)请在坐标系中画出二次函数 y=x2-2x的大致图象;(2)根据方程的根与函数图象的关系,将方程 x2-2x=1 的根在图上近似的表示出来(描点);(3)观察图象,直接写出方程 x2-2x=1 的根(精确到 0.1).图 22-2-2解:(1)如图 D5,y=x2-2x=(x-1)2-1,作出顶点,作出与 x 轴的交点,图象光滑.
(2)正确作出点 M,N.
(3)方程的根为-0.4,2.4.图 D5知识点 3二次函数与一元二次不等式的关系 【例 3】二次函数 y=ax2+bx+c(a≠0)的图象如图 22-2-3,
根据图象回答下列问题:
(1)写出关于 x 的不等式 ax2+bx+c>0 的解集;
(2)写出关于 x 的不等式 ax2+bx+c<0 的解集.
图 22-2-3 思路点拨:ax2 +bx +c>0 的解集就是二次函数 y =ax2 +
bx +c 的图象在 x 轴上方的部分所对应的 x 的取值;反之,
ax2 +bx+c<0 的解集就是二次函数 y=ax2 +bx+c 的图象在 x
轴下方的部分所对应的 x 的取值.解:(1)不等式 ax2+bx+c>0 的解集为{x|1(2)不等式 ax2+bx+c<0 的解集为{x|x<1 或 x>3}.以 a>0 为例列表如下:【跟踪训练】 5.如图 22-2-4,二次函数 y=ax2+bx+c 的图象与 x 轴交于
(1,0),(5,0)两点,那么当 y≥0 时,x 的取值范围_____________.图 22-2-4{x|x<1 或 x>5} 6.如图 22-2-5 是二次函数 y=ax2+bx+c 图象的一部分,
其对称轴为直线 x=1,若其与 x 轴一交点为 A(3,0),则由图象
可知,不等式 ax2+bx+c<0 的解集是__________.图 22-2-5-1<x<3 解析:∵二次函数的对称轴为x=1,与 x 轴的一个交点坐标
为(3,0),则另一个交点坐标为(-1,0).∵不等式ax2+bx+c<0 即
为 y<0 的部分,∴不等式的解集是-1<x<3.
(1)探究:观察图 :图 22-2-1①二次函数 y=x2+x-1 的图象与 x 轴有______个交点,则一元二次方程 x2+x-1=0 的根的判别式Δ______0.2>②二次函数 y=x2-4x+4 的图像与 x 轴有______个交点,则一元二次方程 x2-4x+4=0 的根的判别式Δ______0.1=③二次函数 y=x2-x+2 的图象与 x 轴________公共点,则一元二次方程 x2-x+2=0 的根的判别式Δ______0.无< 归纳:(1)如果抛物线 y=ax2+bx+c 与 x 轴有公共点,公
共点的横坐标是 x0,那么当 x=x0 时,函数的值是____,因此
x=x0 就是方程______________的一个根.0ax2+bx+c=0(2)如下表:
两两一一00 2.利用函数图象求一元二次方程的根
步骤:
(1)作函数图象;
(2)确定根所在的________;
(3)通过取________的方法不断缩小根所在的范围,直至符
合题目要求.范围平均数知识点 1二次函数与一元二次方程的关系 【例 1】 已知二次函数 y=mx2-6x+1(m 是常数)的图象与
x 轴只有一个交点,求 m 的值.
思路点拨:“只有一个交点”等价于“方程只有一个根”.
解:当 m=0 时,函数 y=-6x+1 的图象与 x 轴只有一个
交点,当m≠0 时,∵函数 y=mx2-6x+1的图象与 x 轴只有一
个交点,
∴方程 mx2-6x+1=0 有两个相等的实数根.
∴(-6)2-4m=0,解得 m=9.
故 m 的值为 0 或 9.【跟踪训练】C1.函数 y=x2-2x-1 的图象,与 x 轴的交点个数有()A.0 个B.1 个C.2 个D.3 个2.若抛线 y=(a-1)x2+2x+1 与 x 轴只有一个交点,则 a的值为________.2知识点 2利用函数图象求一元二次方程的近似解 【例 2】 利用二次函数的图象,求方程 x2+2x-10=0 的
近似根(精确到 0.1).
思路点拨:先借助二次函数图象确定方程的解的大致范围,
再通过计算进一步精确.
解:作二次函数 y=x2+2x-10 的图象如图 D4,由图象可
知方程 x2+2x-10=0 有两个根,一个在-5 和-4 之间,一个
在 2 和 3 之间.因此两个根分别为-4 点几和 2 点几,下面用
计算器进行探索.因此 x=-4.3 是方程的一个近似根.
另一个根也可以类似地求出:因此 x=2.3 是方程的另一个近似根.图D43.已知 y=x2+2x-10,小明计算器列出了下表:那么 x2+2x-10=0 一个根是()CA.-4.1B.-4.2C.-4.3D.-4.44.如图 22-2-2,(1)请在坐标系中画出二次函数 y=x2-2x的大致图象;(2)根据方程的根与函数图象的关系,将方程 x2-2x=1 的根在图上近似的表示出来(描点);(3)观察图象,直接写出方程 x2-2x=1 的根(精确到 0.1).图 22-2-2解:(1)如图 D5,y=x2-2x=(x-1)2-1,作出顶点,作出与 x 轴的交点,图象光滑.
(2)正确作出点 M,N.
(3)方程的根为-0.4,2.4.图 D5知识点 3二次函数与一元二次不等式的关系 【例 3】二次函数 y=ax2+bx+c(a≠0)的图象如图 22-2-3,
根据图象回答下列问题:
(1)写出关于 x 的不等式 ax2+bx+c>0 的解集;
(2)写出关于 x 的不等式 ax2+bx+c<0 的解集.
图 22-2-3 思路点拨:ax2 +bx +c>0 的解集就是二次函数 y =ax2 +
bx +c 的图象在 x 轴上方的部分所对应的 x 的取值;反之,
ax2 +bx+c<0 的解集就是二次函数 y=ax2 +bx+c 的图象在 x
轴下方的部分所对应的 x 的取值.解:(1)不等式 ax2+bx+c>0 的解集为{x|1
(1,0),(5,0)两点,那么当 y≥0 时,x 的取值范围_____________.图 22-2-4{x|x<1 或 x>5} 6.如图 22-2-5 是二次函数 y=ax2+bx+c 图象的一部分,
其对称轴为直线 x=1,若其与 x 轴一交点为 A(3,0),则由图象
可知,不等式 ax2+bx+c<0 的解集是__________.图 22-2-5-1<x<3 解析:∵二次函数的对称轴为x=1,与 x 轴的一个交点坐标
为(3,0),则另一个交点坐标为(-1,0).∵不等式ax2+bx+c<0 即
为 y<0 的部分,∴不等式的解集是-1<x<3.
