函数y=Asin(ωx+φ)图像

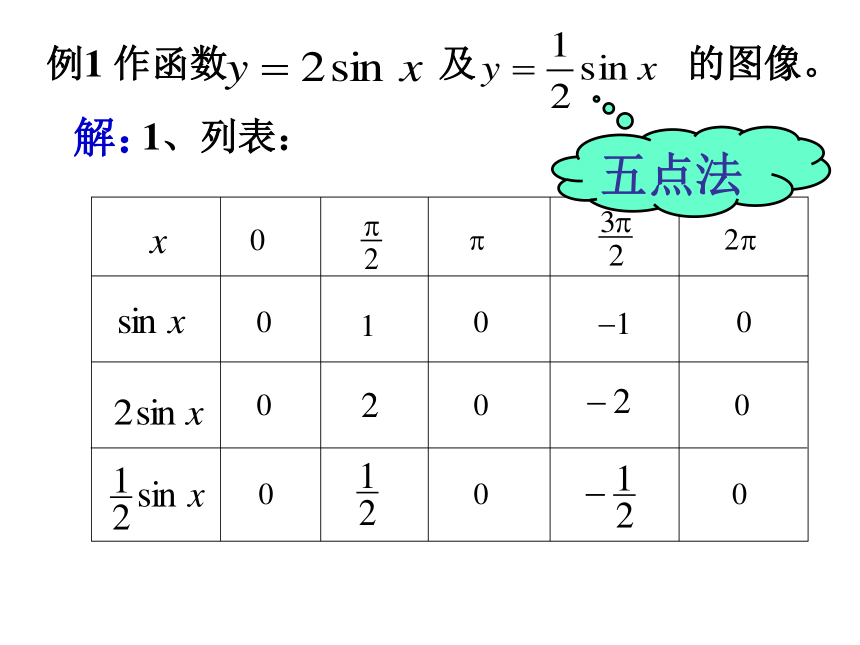
课件35张PPT。§1.8函数y=Asin(ωx+φ)的图像 内乡一中1、列表：x例1 作函数 及 的图像。 解：五点法
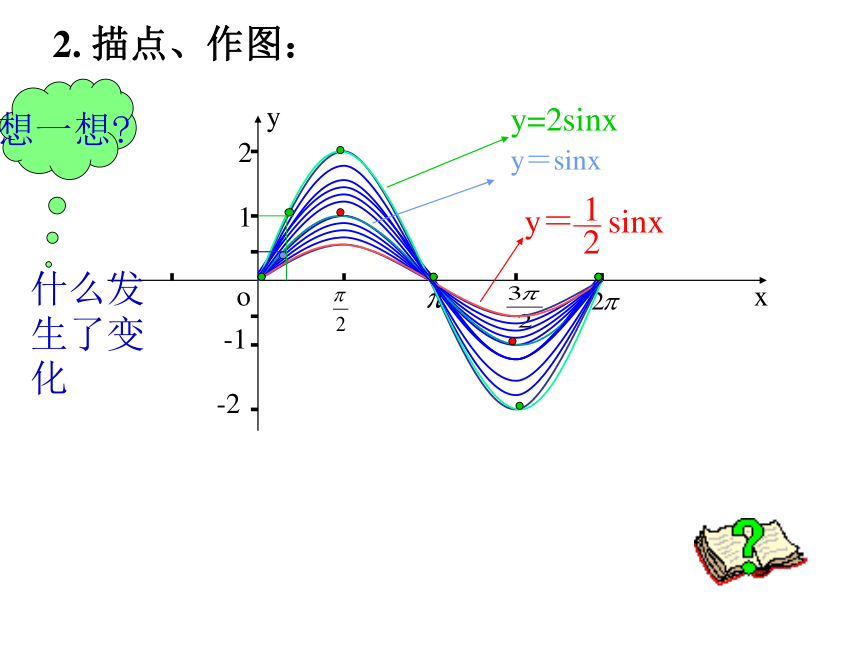
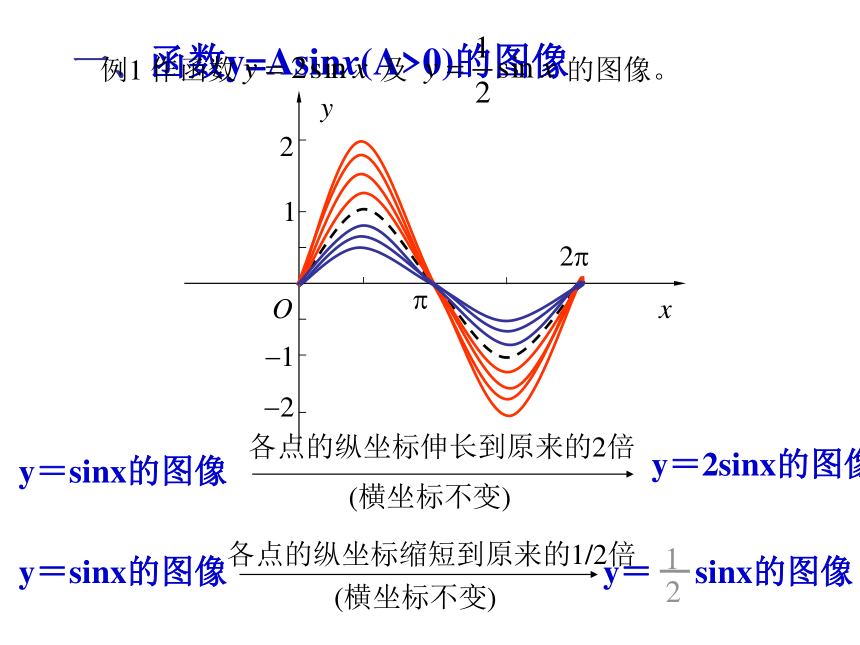
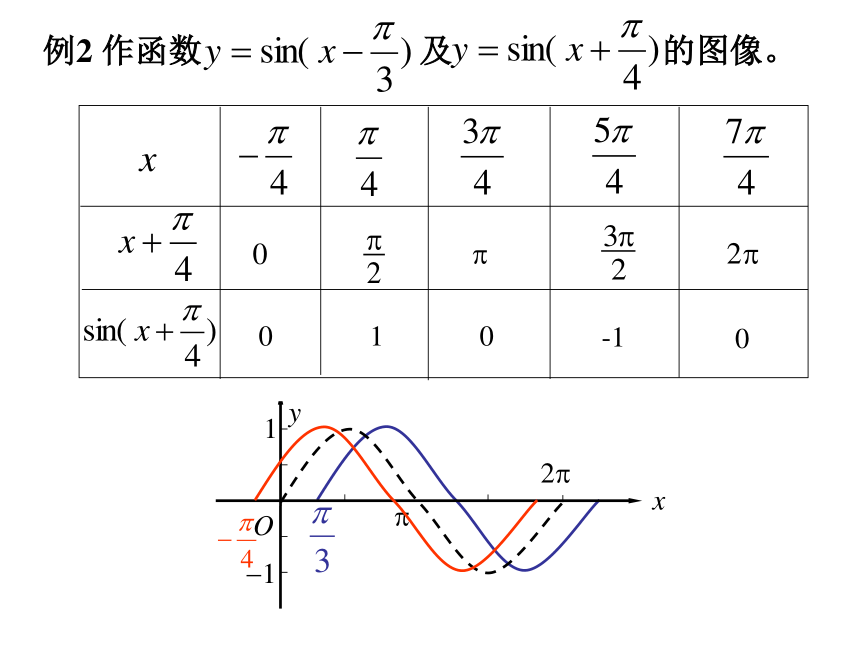
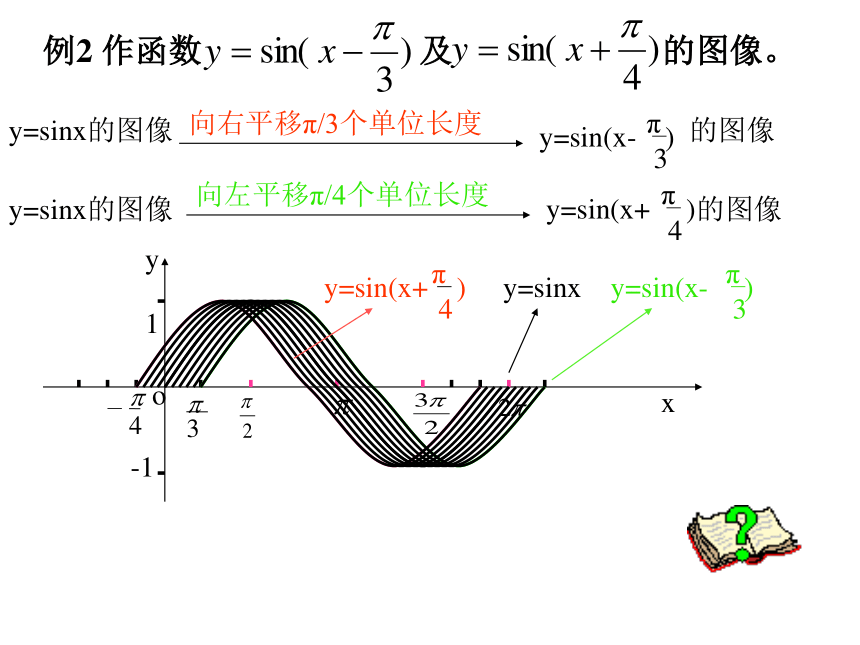
y=2sinxy＝sinx想一想?什么发生了变化2. 描点、作图：xyO?2?12?2?1一、函数y=Asinx(A>0)的图像例1 作函数 及 的图像。 各点的纵坐标伸长到原来的2倍(横坐标不变)各点的纵坐标缩短到原来的1/2倍(横坐标不变) 函数y=Asinx (A >0且A≠1)的图像可以看作是把 y=sinx 的图像上所有点的纵坐标伸长 (当A>1时)或缩短(当00)的图像练习：作下列函数在长度为一个周期的闭区间上的简图：A叫振幅，这种变换叫振幅变换例2 作函数 及 的图像。 xy向右平移π/3个单位长度向左平移π/4个单位长度y=sinx例2 作函数 及 的图像。 函数y=sin(x+φ) 的图像可以看作是把 y=sinx 的图像上所有的点向左(当φ>0时)或向右(当φ<0时)平移|φ|个单位而得到的。二、函数y=sin(x+φ)图像相位变换, φ叫初相, x+φ叫相位1、为得到ｙ＝４sin(2x+　　)，x∈ R，的图像，只需将函数ｙ＝2sin(2x+　　)，x∈ R的图像上所有点( )
(A)横坐标变为原来的２倍，纵坐标不变
(B)横坐标变为原来的　倍，纵坐标不变
(C)纵坐标变为原来的２倍，横坐标不变
(D)纵坐标变为原来的　倍，横坐标不变C课 堂 练 习2、将函数y=3sinx的图像向右平移 个单位长度，得到函数的解析式为: 。 3、为得到函数ｙ＝sin(2x-- ),x ∈ R，的图像，只需将函数ｙ＝sin2x, x ∈ R，的图像上所有点( )
(A)向左平移 个单位长度
(B)向右平移 个单位长度
(C)向左平移 个单位长度
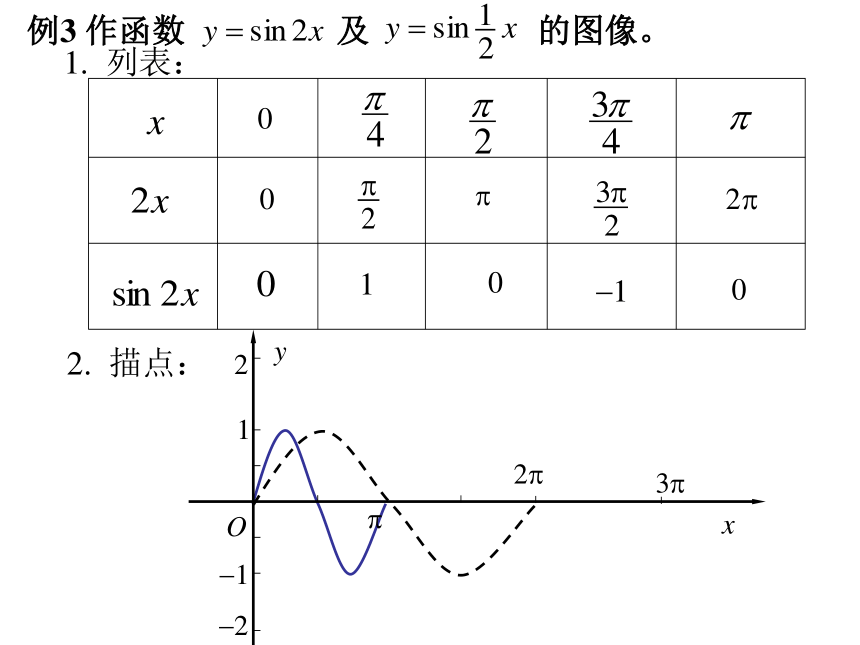
(D)向右平移 个单位长度B1. 列表：例3 作函数 及 的图像。 2. 描点：1. 列表：2. 描点：０　　１　　　０　　－１　　０三、函数y=sin?x(?>0)图像y=sinx的图像 y=sin2x的图像各点的横坐标缩短到原来的1/2倍y=sinx的图像 y=sin x的图像各点的横坐标伸长到原来的2倍(纵坐标不变)(纵坐标不变) 函数y=sin?x (? >0且?≠1)的图像可以看作是把 y=sinx 的图像上所有点的横坐标缩短(当?>1时)或伸长(当00)图像这种变换叫周期变换?决定了函数的周期T= ,通常周期的倒数f= 叫频率.xO?2?1?13?4?法一：法一：法二：例4 作函数 及 的图像。 x例4 作函数 及 的图像。 四、函数y=sin(ωx+φ)与y=sinωx图像的关系四、函数y=sin(ωx+φ)与y=sinωx图像的关系 函数y=sin(ωx+φ) 的图像可以看作是把 y=sinωx 的图像上所有的点向左(当φ>0时)或向右(当φ<0时)平
移| |个单位而得到的。复习回顾：一、怎样通过变换得到函数y=Asinx(A>0)
的图像？ 函数y=Asinx (A >0且A≠1)的图像可以看作是把 y=sinx 的图像上所有点的纵坐标伸长 (当A>1时)或缩短(当00时)或向右(当φ<0时)平移|φ|个单位而得到的。二、怎样通过变换得到函数y=sin(x+φ)
的图像？可以通过相位变换复习回顾： 函数y=sin?x (? >0且?≠1)的图像可以看作是把 y=sinx 的图像上所有点的横坐标缩短(当?>1时)或伸长(当0的图像？可以通过周期变换复习回顾：例5 作函数 y = 3sin(2 + )的简图解：1、列表2??2、 描点,连线函数 y=sinx y=sin(x+ ) 的图像（1）向左平移 先平移后伸缩方法一: 先平移后伸缩例5 作函数 y = 3sin(2 + )的简图解：1、列表2??2、 描点,连线（2）向左平移
先伸缩后平移方法二:先伸缩后平移1、为得到ｙ＝２sin(　x -- 　)，x∈ R，的图像，只需将函数ｙ＝２sin(x－　)，x∈ R的图像上所有点( )
(A)横坐标变为原来的２倍，纵坐标不变
(B)横坐标变为原来的　倍，纵坐标不变
(C)纵坐标变为原来的２倍，横坐标不变
(D)纵坐标变为原来的　倍，横坐标不变Ａ课 堂 练 习2、将函数y=2sin（x+　）的图像上所有点的横坐标变为原来的２倍，纵坐标不变，得到的函数的解析式为: 。 3、将函数y=sinx的图像上所有点的横坐标变为原来的３倍，纵坐标不变，再将所得函数图像向左平移 　 个单位长度，得到的函数的解析式为: 。作业：课本P54页习题1-8