2.2.2向量的减法

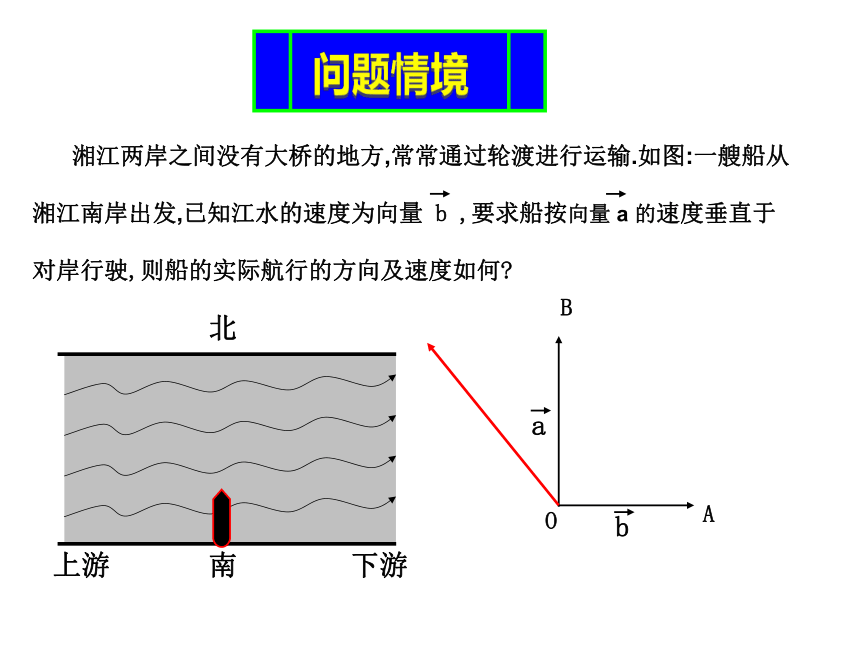
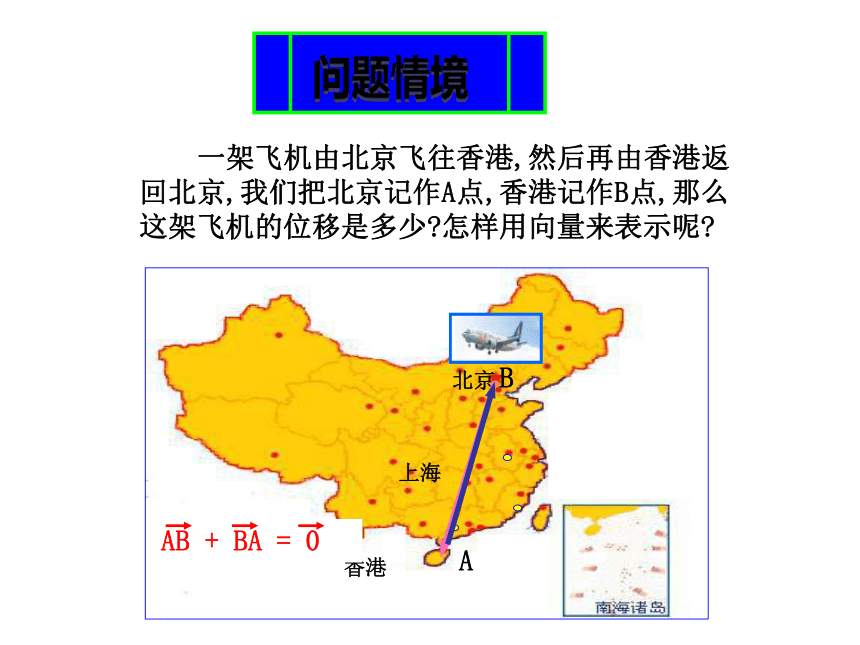
课件19张PPT。2.2.1向量减法运算问题情境 一架飞机由北京飞往香港,然后再由香港返
回北京,我们把北京记作A点,香港记作B点,那么
这架飞机的位移是多少?怎样用向量来表示呢?北京香港上海BA 长度相等,方向相反ABDEABAB DC点拨1.能运用向量的加减法的几何意义从"数"的角度
分析和解决问题;
2.化简时注意向量的加法与减法的相互转化.
ABCDABCD图(1)图(2)2.如图:已知一点O到平行四边形ABCD的3个顶点 A、B、C
的向量分别是 a 、b 、c ,则向量 OD 等于( )

A.a + b + c B.a - b + c

C.a + b - c D.a - b - c
B点拨1.能运用向量的加减法的几何意义从"形"的角度
分析和解决问题;
2.利用向量加减法的几何意义构造几何图形,转化
为几何问题,这就是数形结合思想的体现.1.如图: D、E、F分别是三角形ABC的边AB、BC、CA

的中点,则 AF - DB 等于( )

A.FD B.FC C.FE D.BE
ADBECFAD·ABCOD 探究:反之也成立吗?E1.数学知识:

相反向量,向量减法的定义,向量减法的几何意义
2.重点、难点:

向量减法的几何意义及应用
3.数学思想:
相互转化,数形结合,分类讨论
课堂新坐标D课后思考: