华师大版九年级上册第24章解直角三角形单元考试题(含答案)
文档属性
| 名称 | 华师大版九年级上册第24章解直角三角形单元考试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 171.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-15 21:06:12 | ||
图片预览



文档简介
华师大版九年级上册第24章解直角三角形单元考试题
姓名: ,成绩: ;
一、选择题(4×12=48分)
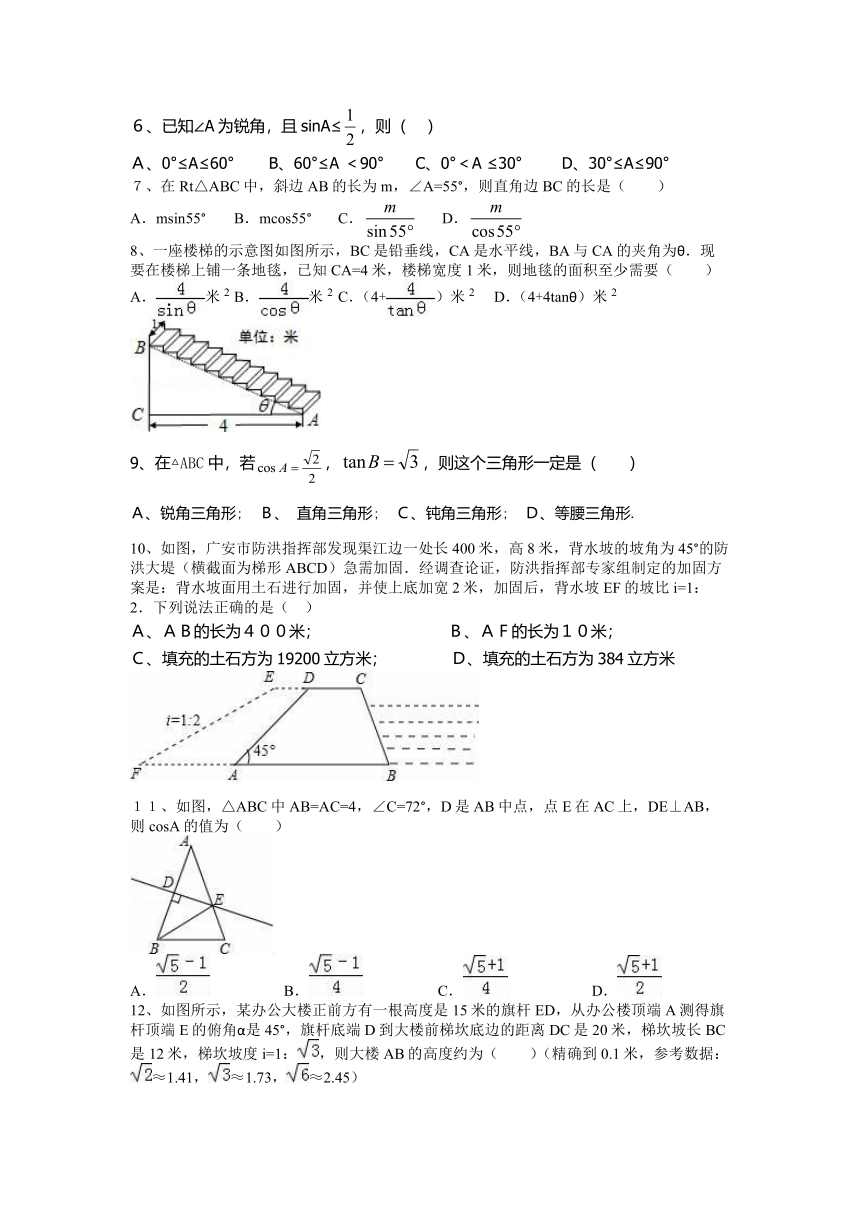
1、将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( )
A.
3cm
B.
6cm
C.
cm
D.
cm
2、如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为( )
A.
B.
C.
D.
3、在Rt△ABC中,∠C=90°,则表示( )
A.sinA
B.cosA
C.sinB
D.以上都不
4、小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出67.5°的角的正切值是(
)
A.+1
B.
+1
C.
2.5
D.
5、在Rt△ABC中,∠C=90°,若tanA=,则sinA=(
)
B、
C、
D、
6、已知∠A为锐角,且sinA≤,则(
)
A、0°≤A≤60°
B、60°≤A
<90° C、0°<A
≤30°
D、30°≤A≤90°
7、在Rt△ABC中,斜边AB的长为m,∠A=55°,则直角边BC的长是( )
A.msin55°
B.mcos55°
C.
D.
8、一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )
A.米2
B.米2
C.(4+)米2
D.(4+4tanθ)米2
9、在△ABC中,若,,则这个三角形一定是(
)
A、锐角三角形; B、
直角三角形; C、钝角三角形; D、等腰三角形.
10、如图,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45°的防洪大堤(横截面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF的坡比i=1:2.下列说法正确的是( )
A、AB的长为400米; B、AF的长为10米;
C、填充的土石方为19200立方米; D、填充的土石方为384立方米
11、如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA的值为( )
A.
B.
C.
D.
12、如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:,则大楼AB的高度约为( )(精确到0.1米,参考数据:≈1.41,≈1.73,≈2.45)
A.30.6
B.32.1
C.37.9
D.39.4
二、填空题(4×6=24分)
13、直角三角形斜边上的中线长是2.5,一直角边的长是3,则此直角三角形的面积为 .
14、如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值是
.
15、若某人沿坡度i=3:4的斜坡前进10m,则他所在的位置比原来的的位置
升高
m。6
16、已知P(2,3),OP与x轴所夹锐角为,则tan=_______
.
17、观察下列等式
①sin30°=
cos60°=
②sin45°=
cos=45°=
③sin60°=
cos30°=
根据上述规律,计算sin2a+sin2(90°﹣a)= .
18、我国为了维护队钓鱼岛P的主权,决定对钓鱼岛进行常态化的立体巡航.在一次巡航中,轮船和飞机的航向相同(AP∥BD),当轮船航行到距钓鱼岛20km的A处时,飞机在B处测得轮船的俯角是45°;当轮船航行到C处时,飞机在轮船正上方的E处,此时EC=5km.轮船到达钓鱼岛P时,测得D处的飞机的仰角为30°.飞机的飞行距离
BD=
(结果保留根号).
三、解答题(7×2=14分)
19、计算:
+tan30°·sin60°
20、如图,在△ABC中,∠A=30°,∠B=45°,AC=,求AB的长。
四、解答题(10×4=40分)
22、如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上)
⑴求教学楼AB的高度;
⑵学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).
(参考数据:sin22°≈,cos22°≈,tan22°≈
)
23、台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力,如图,据气象观测,距沿海某城市A的正南方向220千米B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级,该台风中心现正以15千米/时的速度沿北偏东30 方向往C移动,且台风中心风力不变,若城市所受风力达到或走过四级,则称为受台风影响.
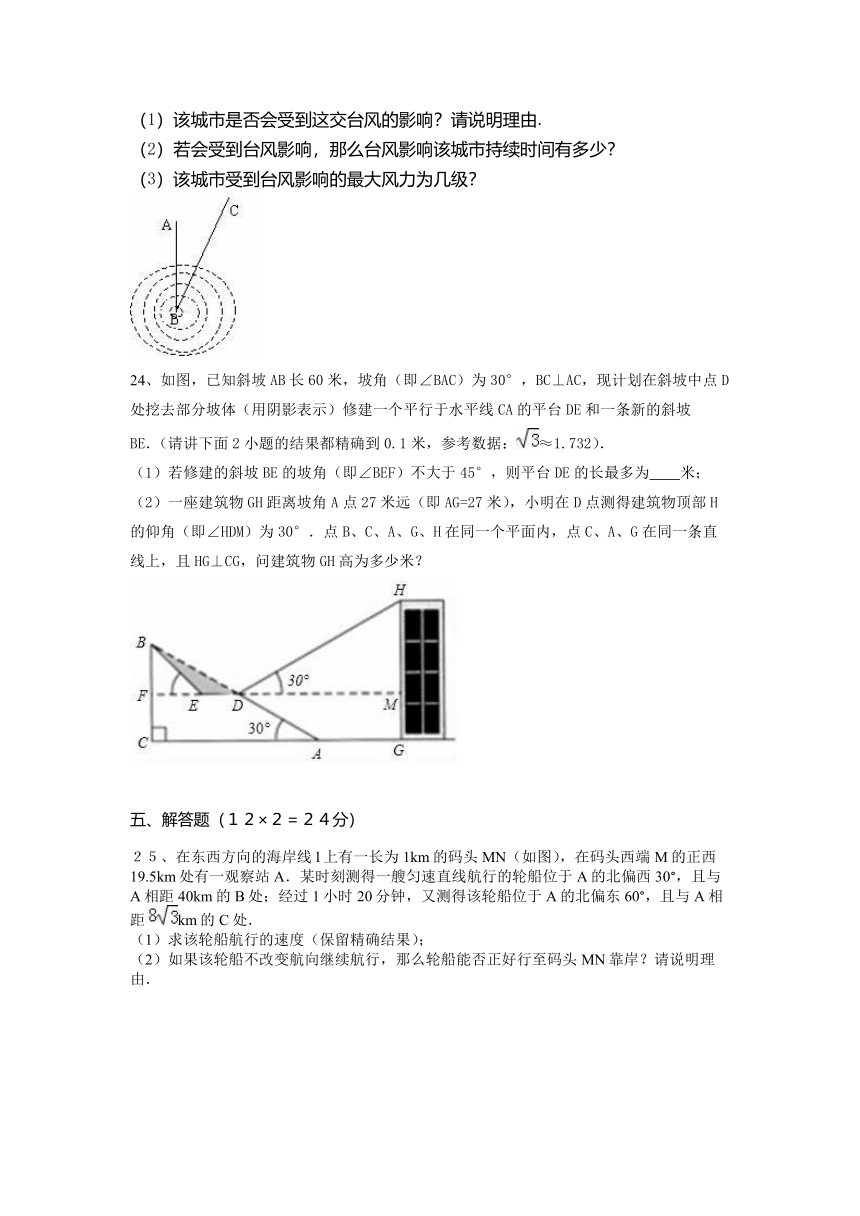
(1)该城市是否会受到这交台风的影响?请说明理由.
(2)若会受到台风影响,那么台风影响该城市持续时间有多少?
(3)该城市受到台风影响的最大风力为几级?
24、如图,已知斜坡AB长60米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.(请讲下面2小题的结果都精确到0.1米,参考数据:≈1.732).
(1)若修建的斜坡BE的坡角(即∠BEF)不大于45°,则平台DE的长最多为 米;
(2)一座建筑物GH距离坡角A点27米远(即AG=27米),小明在D点测得建筑物顶部H的仰角(即∠HDM)为30°.点B、C、A、G、H在同一个平面内,点C、A、G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?
五、解答题(12×2=24分)
25、在东西方向的海岸线l上有一长为1km的码头MN(如图),在码头西端M的正西19.5km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距km的C处.
(1)求该轮船航行的速度(保留精确结果);
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.
26、已知:如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=6,AB=3.E为BC边上一点,以BE为边作正方形BEFG,使正方形BEFG和梯形ABCD在BC的同侧.
(1)当正方形的顶点F恰好落在对角线AC上时,求BE的长;
(2)将(1)问中的正方形BEFG沿BC向右平移,记平移中的正方形BEFC为正方形B′EFG,当点E与点C重合时停止平移.设平移的距离为t,正方形B′EFG的边EF与AC交于点M,连接B′D,B′M,DM,是否存在这样的t,使△B′DM是直角三角形?若存在,求出t的值;若不存在,请说明理由;
(3)在(2)问的平移过程中,设正方形B′EFG与△ADC重叠部分的面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围.
华师大版九年级上册第24章解直角三角形单元考试题的答案
一、选择题
DBABD
CADAC
CD
二、填空题
13、6,
14、2,
15、6,
16、
1.5,
17、
1,
18、25+5
三、解答题
19、2
20、3+
四、解答题
22、⑴过点E作EM⊥AB,垂足为M.设AB为x.
Rt△ABF中,∠AFB=45°,∴BF=AB=x,∴BC=BF+FC=x+13
在Rt△AEM中,∠AEM=22°,AM=AB-BM=AB-CE=x-2,∴tan22°=
,
=,x=12.即教学楼的高12m.
⑵由(1)可得ME=BC=x+13=12+13=25.在Rt△AME中,cos22°= ,
∴AE= ≈
EQ
\f(25,)≈27.即AE之间的距离约为27m.
23、(1)由点A作AD⊥BC于D,
则AD就为城市A距台风中心的最短距离
在Rt△ABD中,∠B=30 ,AB=220,
∴AD=AB=110.
由题意知,当A点距台风(12-4)20=160(千米)时,将会受到台风影响.
故该城市会受到这次台风的影响.
(2)由题意知,当A点距台风中心不超过60千米时,
将会受到台风的影响,则AE=AF=160.当台风中心从E到F处时,
该城市都会受到这次台风的影响.
由勾股定理得
∴EF=2DE=6.
因为这次台风中心以15千米/时的速度移动,
所以这次台风影响该城市的持续时间为小时.
(3)当台风中心位于D处时,A城市所受这次台风的风力最大,其最大风力为12-=6.5级.
24、(1)∵修建的斜坡BE的坡角(即∠BEF)不大于45°,
∴∠BEF最大为45°,
当∠BEF=45°时,EF最短,此时ED最长,
∵∠DAC=∠BDF=30°,AD=BD=30,
∴BF=EF=BD=15,
DF=15,
故:DE=DF﹣EF=15(﹣1)≈11.0;
(2)过点D作DP⊥AC,垂足为P.
在Rt△DPA中,DP=AD=×30=15,
PA=ADcos30°=×30=15.
在矩形DPGM中,MG=DP=15,DM=PG=15+27,
在Rt△DMH中,
HM=DMtan30°=×(15+27)=15+9.
GH=HM+MG=15+15+9≈45.6.
答:建筑物GH高为45.6米.
五、解答题
25、(1)∵∠1=30°,∠2=60°,
∴△ABC为直角三角形.
∵AB=40km,AC=km,
∴BC===16(km).
∵1小时20分钟=80分钟,1小时=60分钟,
∴×60=12(千米/小时).
(2)作线段BR⊥x轴于R,作线段CS⊥x轴于S,延长BC交l于T.
∵∠2=60°,
∴∠4=90°﹣60°=30°.
∵AC=8(km),
∴CS=8sin30°=4(km).
∴AS=8cos30°=8×=12(km).
又∵∠1=30°,
∴∠3=90°﹣30°=60°.
∵AB=40km,
∴BR=40sin60°=20(km).
∴AR=40×cos60°=40×=20(km).
易得,△STC∽△RTB,
所以=,
,
解得:ST=8(km).
所以AT=12+8=20(km).
又因为AM=19.5km,MN长为1km,∴AN=20.5km,
∵19.5<AT<20.5
故轮船能够正好行至码头MN靠岸.
26、(1)如图①,
设正方形BEFG的边长为x,
则BE=FG=BG=x,
∵AB=3,BC=6,
∴AG=AB﹣BG=3﹣x,
∵GF∥BE,
∴△AGF∽△ABC,
∴,
即,
解得:x=2,
即BE=2;
(2)存在满足条件的t,
理由:如图②,过点D作DH⊥BC于H,
则BH=AD=2,DH=AB=3,
由题意得:BB′=HE=t,HB′=|t﹣2|,EC=4﹣t,
∵EF∥AB,
∴△MEC∽△ABC,
∴,即,
∴ME=2﹣t,
在Rt△B′ME中,B′M2=ME2+B′E2=22+(2﹣t)2=t2﹣2t+8,
在Rt△DHB′中,B′D2=DH2+B′H2=32+(t﹣2)2=t2﹣4t+13,
过点M作MN⊥DH于N,
则MN=HE=t,NH=ME=2﹣t,
∴DN=DH﹣NH=3﹣(2﹣t)=t+1,
在Rt△DMN中,DM2=DN2+MN2=t2+t+1,
(Ⅰ)若∠DB′M=90°,则DM2=B′M2+B′D2,
即t2+t+1=(t2﹣2t+8)+(t2﹣4t+13),
解得:t=,
(Ⅱ)若∠B′MD=90°,则B′D2=B′M2+DM2,
即t2﹣4t+13=(t2﹣2t+8)+(t2+t+1),
解得:t1=﹣3+,t2=﹣3﹣(舍去),
∴t=﹣3+;
(Ⅲ)若∠B′DM=90°,则B′M2=B′D2+DM2,
即:
t2﹣2t+8=(t2﹣4t+13)+(t2+t+1),
此方程无解,
综上所述,当t=或﹣3+时,△B′DM是直角三角形;
(3)①如图③,当F在CD上时,EF:DH=CE:CH,
即2:3=CE:4,
∴CE=,
∴t=BB′=BC﹣B′E﹣EC=6﹣2﹣=,
∵ME=2﹣t,
∴FM=t,
当0≤t≤时,S=S△FMN=×t×t=t2,
②如图④,当G在AC上时,t=2,
∵EK=ECtan∠DCB=EC=(4﹣t)=3﹣t,
∴FK=2﹣EK=t﹣1,
∵NL=AD=,
∴FL=t﹣,
∴当<t≤2时,S=S△FMN﹣S△FKL=t2﹣(t﹣)(t﹣1)=﹣t2+t﹣;
③如图⑤,当G在CD上时,B′C:CH=B′G:DH,
即B′C:4=2:3,
解得:B′C=,
∴EC=4﹣t=B′C﹣2=,
∴t=,
∵B′N=B′C=(6﹣t)=3﹣t,
∵GN=GB′﹣B′N=t﹣1,
∴当2<t≤时,S=S梯形GNMF﹣S△FKL=×2×(t﹣1+t)﹣(t﹣)(t﹣1)=﹣t2+2t﹣,
④如图⑥,当<t≤4时,
∵B′L=B′C=(6﹣t),EK=EC=(4﹣t),B′N=B′C=(6﹣t),EM=EC=(4﹣t),
S=S梯形MNLK=S梯形B′EKL﹣S梯形B′EMN=﹣t+.
综上所述:
当0≤t≤时,S=t2,
当<t≤2时,S=﹣t2+t﹣;
当2<t≤时,S=﹣t2+2t﹣,
当<t≤4时,S=﹣t+.
C
B
A
姓名: ,成绩: ;
一、选择题(4×12=48分)
1、将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( )
A.
3cm
B.
6cm
C.
cm
D.
cm
2、如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为( )
A.
B.
C.
D.
3、在Rt△ABC中,∠C=90°,则表示( )
A.sinA
B.cosA
C.sinB
D.以上都不
4、小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以求出67.5°的角的正切值是(
)
A.+1
B.
+1
C.
2.5
D.
5、在Rt△ABC中,∠C=90°,若tanA=,则sinA=(
)
B、
C、
D、
6、已知∠A为锐角,且sinA≤,则(
)
A、0°≤A≤60°
B、60°≤A
<90° C、0°<A
≤30°
D、30°≤A≤90°
7、在Rt△ABC中,斜边AB的长为m,∠A=55°,则直角边BC的长是( )
A.msin55°
B.mcos55°
C.
D.
8、一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )
A.米2
B.米2
C.(4+)米2
D.(4+4tanθ)米2
9、在△ABC中,若,,则这个三角形一定是(
)
A、锐角三角形; B、
直角三角形; C、钝角三角形; D、等腰三角形.
10、如图,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45°的防洪大堤(横截面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF的坡比i=1:2.下列说法正确的是( )
A、AB的长为400米; B、AF的长为10米;
C、填充的土石方为19200立方米; D、填充的土石方为384立方米
11、如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA的值为( )
A.
B.
C.
D.
12、如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:,则大楼AB的高度约为( )(精确到0.1米,参考数据:≈1.41,≈1.73,≈2.45)
A.30.6
B.32.1
C.37.9
D.39.4
二、填空题(4×6=24分)
13、直角三角形斜边上的中线长是2.5,一直角边的长是3,则此直角三角形的面积为 .
14、如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值是
.
15、若某人沿坡度i=3:4的斜坡前进10m,则他所在的位置比原来的的位置
升高
m。6
16、已知P(2,3),OP与x轴所夹锐角为,则tan=_______
.
17、观察下列等式
①sin30°=
cos60°=
②sin45°=
cos=45°=
③sin60°=
cos30°=
根据上述规律,计算sin2a+sin2(90°﹣a)= .
18、我国为了维护队钓鱼岛P的主权,决定对钓鱼岛进行常态化的立体巡航.在一次巡航中,轮船和飞机的航向相同(AP∥BD),当轮船航行到距钓鱼岛20km的A处时,飞机在B处测得轮船的俯角是45°;当轮船航行到C处时,飞机在轮船正上方的E处,此时EC=5km.轮船到达钓鱼岛P时,测得D处的飞机的仰角为30°.飞机的飞行距离
BD=
(结果保留根号).
三、解答题(7×2=14分)
19、计算:
+tan30°·sin60°
20、如图,在△ABC中,∠A=30°,∠B=45°,AC=,求AB的长。
四、解答题(10×4=40分)
22、如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上)
⑴求教学楼AB的高度;
⑵学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).
(参考数据:sin22°≈,cos22°≈,tan22°≈
)
23、台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力,如图,据气象观测,距沿海某城市A的正南方向220千米B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级,该台风中心现正以15千米/时的速度沿北偏东30 方向往C移动,且台风中心风力不变,若城市所受风力达到或走过四级,则称为受台风影响.
(1)该城市是否会受到这交台风的影响?请说明理由.
(2)若会受到台风影响,那么台风影响该城市持续时间有多少?
(3)该城市受到台风影响的最大风力为几级?
24、如图,已知斜坡AB长60米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.(请讲下面2小题的结果都精确到0.1米,参考数据:≈1.732).
(1)若修建的斜坡BE的坡角(即∠BEF)不大于45°,则平台DE的长最多为 米;
(2)一座建筑物GH距离坡角A点27米远(即AG=27米),小明在D点测得建筑物顶部H的仰角(即∠HDM)为30°.点B、C、A、G、H在同一个平面内,点C、A、G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?
五、解答题(12×2=24分)
25、在东西方向的海岸线l上有一长为1km的码头MN(如图),在码头西端M的正西19.5km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距km的C处.
(1)求该轮船航行的速度(保留精确结果);
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.
26、已知:如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=6,AB=3.E为BC边上一点,以BE为边作正方形BEFG,使正方形BEFG和梯形ABCD在BC的同侧.
(1)当正方形的顶点F恰好落在对角线AC上时,求BE的长;
(2)将(1)问中的正方形BEFG沿BC向右平移,记平移中的正方形BEFC为正方形B′EFG,当点E与点C重合时停止平移.设平移的距离为t,正方形B′EFG的边EF与AC交于点M,连接B′D,B′M,DM,是否存在这样的t,使△B′DM是直角三角形?若存在,求出t的值;若不存在,请说明理由;
(3)在(2)问的平移过程中,设正方形B′EFG与△ADC重叠部分的面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围.
华师大版九年级上册第24章解直角三角形单元考试题的答案
一、选择题
DBABD
CADAC
CD
二、填空题
13、6,
14、2,
15、6,
16、
1.5,
17、
1,
18、25+5
三、解答题
19、2
20、3+
四、解答题
22、⑴过点E作EM⊥AB,垂足为M.设AB为x.
Rt△ABF中,∠AFB=45°,∴BF=AB=x,∴BC=BF+FC=x+13
在Rt△AEM中,∠AEM=22°,AM=AB-BM=AB-CE=x-2,∴tan22°=
,
=,x=12.即教学楼的高12m.
⑵由(1)可得ME=BC=x+13=12+13=25.在Rt△AME中,cos22°= ,
∴AE= ≈
EQ
\f(25,)≈27.即AE之间的距离约为27m.
23、(1)由点A作AD⊥BC于D,
则AD就为城市A距台风中心的最短距离
在Rt△ABD中,∠B=30 ,AB=220,
∴AD=AB=110.
由题意知,当A点距台风(12-4)20=160(千米)时,将会受到台风影响.
故该城市会受到这次台风的影响.
(2)由题意知,当A点距台风中心不超过60千米时,
将会受到台风的影响,则AE=AF=160.当台风中心从E到F处时,
该城市都会受到这次台风的影响.
由勾股定理得
∴EF=2DE=6.
因为这次台风中心以15千米/时的速度移动,
所以这次台风影响该城市的持续时间为小时.
(3)当台风中心位于D处时,A城市所受这次台风的风力最大,其最大风力为12-=6.5级.
24、(1)∵修建的斜坡BE的坡角(即∠BEF)不大于45°,
∴∠BEF最大为45°,
当∠BEF=45°时,EF最短,此时ED最长,
∵∠DAC=∠BDF=30°,AD=BD=30,
∴BF=EF=BD=15,
DF=15,
故:DE=DF﹣EF=15(﹣1)≈11.0;
(2)过点D作DP⊥AC,垂足为P.
在Rt△DPA中,DP=AD=×30=15,
PA=ADcos30°=×30=15.
在矩形DPGM中,MG=DP=15,DM=PG=15+27,
在Rt△DMH中,
HM=DMtan30°=×(15+27)=15+9.
GH=HM+MG=15+15+9≈45.6.
答:建筑物GH高为45.6米.
五、解答题
25、(1)∵∠1=30°,∠2=60°,
∴△ABC为直角三角形.
∵AB=40km,AC=km,
∴BC===16(km).
∵1小时20分钟=80分钟,1小时=60分钟,
∴×60=12(千米/小时).
(2)作线段BR⊥x轴于R,作线段CS⊥x轴于S,延长BC交l于T.
∵∠2=60°,
∴∠4=90°﹣60°=30°.
∵AC=8(km),
∴CS=8sin30°=4(km).
∴AS=8cos30°=8×=12(km).
又∵∠1=30°,
∴∠3=90°﹣30°=60°.
∵AB=40km,
∴BR=40sin60°=20(km).
∴AR=40×cos60°=40×=20(km).
易得,△STC∽△RTB,
所以=,
,
解得:ST=8(km).
所以AT=12+8=20(km).
又因为AM=19.5km,MN长为1km,∴AN=20.5km,
∵19.5<AT<20.5
故轮船能够正好行至码头MN靠岸.
26、(1)如图①,
设正方形BEFG的边长为x,
则BE=FG=BG=x,
∵AB=3,BC=6,
∴AG=AB﹣BG=3﹣x,
∵GF∥BE,
∴△AGF∽△ABC,
∴,
即,
解得:x=2,
即BE=2;
(2)存在满足条件的t,
理由:如图②,过点D作DH⊥BC于H,
则BH=AD=2,DH=AB=3,
由题意得:BB′=HE=t,HB′=|t﹣2|,EC=4﹣t,
∵EF∥AB,
∴△MEC∽△ABC,
∴,即,
∴ME=2﹣t,
在Rt△B′ME中,B′M2=ME2+B′E2=22+(2﹣t)2=t2﹣2t+8,
在Rt△DHB′中,B′D2=DH2+B′H2=32+(t﹣2)2=t2﹣4t+13,
过点M作MN⊥DH于N,
则MN=HE=t,NH=ME=2﹣t,
∴DN=DH﹣NH=3﹣(2﹣t)=t+1,
在Rt△DMN中,DM2=DN2+MN2=t2+t+1,
(Ⅰ)若∠DB′M=90°,则DM2=B′M2+B′D2,
即t2+t+1=(t2﹣2t+8)+(t2﹣4t+13),
解得:t=,
(Ⅱ)若∠B′MD=90°,则B′D2=B′M2+DM2,
即t2﹣4t+13=(t2﹣2t+8)+(t2+t+1),
解得:t1=﹣3+,t2=﹣3﹣(舍去),
∴t=﹣3+;
(Ⅲ)若∠B′DM=90°,则B′M2=B′D2+DM2,
即:
t2﹣2t+8=(t2﹣4t+13)+(t2+t+1),
此方程无解,
综上所述,当t=或﹣3+时,△B′DM是直角三角形;
(3)①如图③,当F在CD上时,EF:DH=CE:CH,
即2:3=CE:4,
∴CE=,
∴t=BB′=BC﹣B′E﹣EC=6﹣2﹣=,
∵ME=2﹣t,
∴FM=t,
当0≤t≤时,S=S△FMN=×t×t=t2,
②如图④,当G在AC上时,t=2,
∵EK=ECtan∠DCB=EC=(4﹣t)=3﹣t,
∴FK=2﹣EK=t﹣1,
∵NL=AD=,
∴FL=t﹣,
∴当<t≤2时,S=S△FMN﹣S△FKL=t2﹣(t﹣)(t﹣1)=﹣t2+t﹣;
③如图⑤,当G在CD上时,B′C:CH=B′G:DH,
即B′C:4=2:3,
解得:B′C=,
∴EC=4﹣t=B′C﹣2=,
∴t=,
∵B′N=B′C=(6﹣t)=3﹣t,
∵GN=GB′﹣B′N=t﹣1,
∴当2<t≤时,S=S梯形GNMF﹣S△FKL=×2×(t﹣1+t)﹣(t﹣)(t﹣1)=﹣t2+2t﹣,
④如图⑥,当<t≤4时,
∵B′L=B′C=(6﹣t),EK=EC=(4﹣t),B′N=B′C=(6﹣t),EM=EC=(4﹣t),
S=S梯形MNLK=S梯形B′EKL﹣S梯形B′EMN=﹣t+.
综上所述:
当0≤t≤时,S=t2,
当<t≤2时,S=﹣t2+t﹣;
当2<t≤时,S=﹣t2+2t﹣,
当<t≤4时,S=﹣t+.
C
B
A
