1.1变化率与导数
图片预览







文档简介
课件20张PPT。普通高中课程标准实验教科书(人教A版)
《数学》选修2-2
1.1.1 变化率问题
★☆十七大视点 党的十七大报告提出:“增强发展协
调性,努力实现经济又好又快发展,转变
发展方式取得重大进展,在优化结构、提
高效益、降低消耗、保护环境的基础上,
人均国内生产总值(GDP)到2020年比2000年翻两番
(2000年中国人均GDP856美元,2020年约为3500美元)。” 国家统计局2007年9月18日发布的
《报告》称:党的十六大以来,我国经济
在持续快速增长的同时保持了比较好的稳
定性,2002年我国人均GDP首次超过1000
美元,达到1100美元,在短短的4年内于
2006年达到2010美元,我国由低收入国家
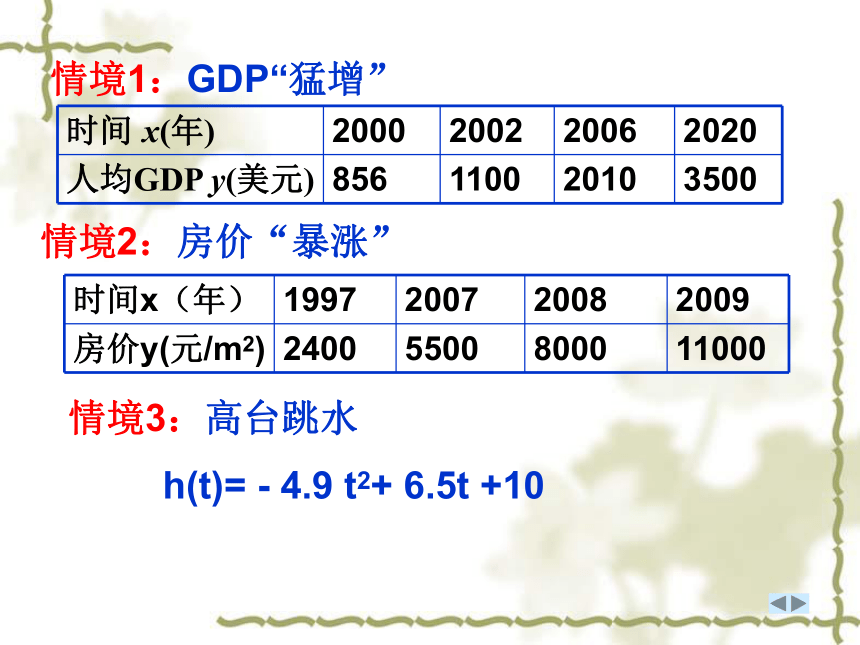
步入中等收入国家的行列。情境1问题1:如何从数学角度刻画2002年至2006年
这4年我国人均GDP“猛增”?910244 2000年至2002年这两年内我国人均GDP平均
每年增加多少美元? 2002年至2006年这四年内我国人均GDP平均
每年增加多少美元?比值反映了在某一时间段内我国人均GDP变化的
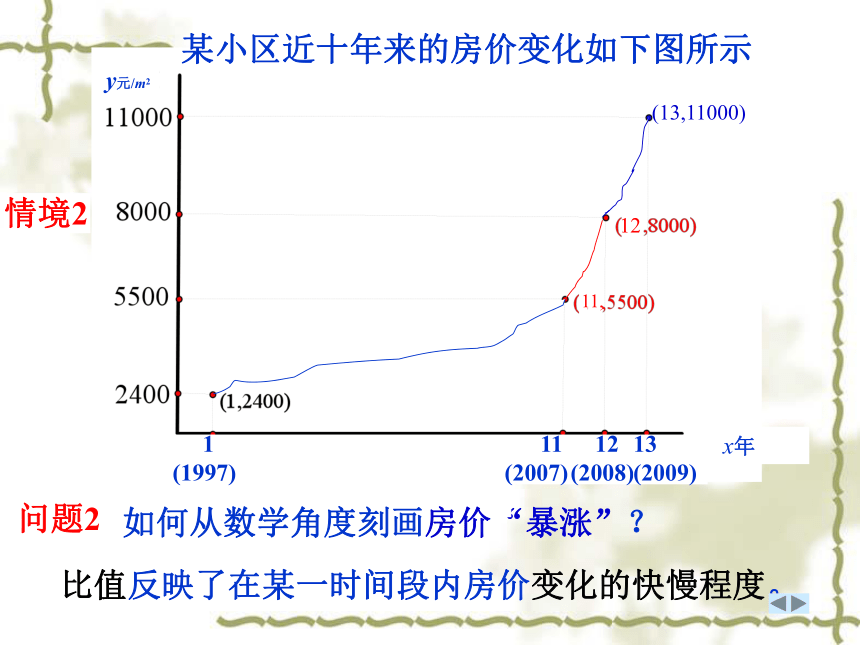
快慢程度? 如何从数学角度刻画房价“暴涨”?情境2问题2某小区近十年来的房价变化如下图所示比值反映了在某一时间段内房价变化的快慢程度。情境3 高台跳水在高台跳水运动中, 运动员相对于水面的高度 h (单位:m)与起跳后的时间 t (单位:s) 存在函数关系:
h(t)= - 4.9 t2+ 6.5t +10播放暂停停止 在高台跳水运动中,运动员相对于水
面的高度h(单位:米)与起跳后的时间t
(单位:s)存在函数关系
h(t)= - 4.9 t2+ 6.5t +10
请计算: 问题3:如何用运动员在某段时间段内
的平均速度粗略地描述其运动状态?
情境1:GDP“猛增”情境2:房价“暴涨”情境3:高台跳水h(t)= - 4.9 t2+ 6.5t +10问题4:用怎样的数学模型刻画函数 值变化的快慢程度? 比值称为函数在某一区间上的平均变化率思考1:你能给出函数 f (x) 从x1到x2的平均变
化率的定义吗?函数 f (x) 从x1到x2的平均变化率为
习惯上:Δx=x2-x1, Δy=f(x2)-f(x1)
则平均变化率为平均变化率为:思考2:平均变化率有什么几何意义呢? 平均变化率的几何意义就是
函数f(x)图像上两点(x1,f(x1)), (x2,f(x2))所在直线的斜率。 在吹气球的过程中, 可发现,随着气球内空气容量的增加, 气球的半径增加得越来越慢. 从数学的角度, 如何描述这种现象呢?活动1:气球膨胀率试分别求:(1)当空气容积V从0L增加到1L时
(2)当空气容积V从1L增加到2L时
气球的平均膨胀率 可以看出:随着气球体积逐渐变大,它的平均膨胀率逐渐变小了。(1)(2)显然0.62>0.16
思考:当空气的容量从V1增加到V2时,气球的平均膨胀率是多少?活动2 试举出生活中与平均变化率有关的例子。探究:如图是函数h(t)= -4.9t2+6.5t+10的图像,计算运动员在 这段时间里的平均速度,并思考以下问题:
1、运动员在这段时间内是静止的吗?
2、你认为用平均速度描述
运动员的运动状态有什
么问题吗?
(1)[1, 3];
(2)[1, 2];
(3)[1, 1.1];
(4)[1, 1.001];
(5)[1, 1.0001]; 一运动质点的位移S与时间t满足S(t)=t2,分别计算S(t)在下列区间上的平均变化率.(位移单位为m,时间单位为s) 432.12.0011.9991.991.92(6)[0.999, 1];
(7)[0.99, 1];
(8)[0.9, 1].2.0001练一练 如何刻画t=1这一时刻
质点运动的快慢程度呢? 思考:2.我想进一步探究的问题是——1.这节课我的收获是——小结:3.这节课我最感兴趣的地方是——1.必做题2.选做题3.思考题课本第10页习题1.1A组:1 已知函数 ,
求 的值: 一运动质点的位移S与时间t满足S(t)=t2, 如何刻画t=1这一时刻质点运动变化的快慢程度呢? (位移单位为m, 时间单位为s) 作业:谢 谢 大 家! 再见!
《数学》选修2-2
1.1.1 变化率问题
★☆十七大视点 党的十七大报告提出:“增强发展协
调性,努力实现经济又好又快发展,转变
发展方式取得重大进展,在优化结构、提
高效益、降低消耗、保护环境的基础上,
人均国内生产总值(GDP)到2020年比2000年翻两番
(2000年中国人均GDP856美元,2020年约为3500美元)。” 国家统计局2007年9月18日发布的
《报告》称:党的十六大以来,我国经济
在持续快速增长的同时保持了比较好的稳
定性,2002年我国人均GDP首次超过1000
美元,达到1100美元,在短短的4年内于
2006年达到2010美元,我国由低收入国家
步入中等收入国家的行列。情境1问题1:如何从数学角度刻画2002年至2006年
这4年我国人均GDP“猛增”?910244 2000年至2002年这两年内我国人均GDP平均
每年增加多少美元? 2002年至2006年这四年内我国人均GDP平均
每年增加多少美元?比值反映了在某一时间段内我国人均GDP变化的
快慢程度? 如何从数学角度刻画房价“暴涨”?情境2问题2某小区近十年来的房价变化如下图所示比值反映了在某一时间段内房价变化的快慢程度。情境3 高台跳水在高台跳水运动中, 运动员相对于水面的高度 h (单位:m)与起跳后的时间 t (单位:s) 存在函数关系:
h(t)= - 4.9 t2+ 6.5t +10播放暂停停止 在高台跳水运动中,运动员相对于水
面的高度h(单位:米)与起跳后的时间t
(单位:s)存在函数关系
h(t)= - 4.9 t2+ 6.5t +10
请计算: 问题3:如何用运动员在某段时间段内
的平均速度粗略地描述其运动状态?
情境1:GDP“猛增”情境2:房价“暴涨”情境3:高台跳水h(t)= - 4.9 t2+ 6.5t +10问题4:用怎样的数学模型刻画函数 值变化的快慢程度? 比值称为函数在某一区间上的平均变化率思考1:你能给出函数 f (x) 从x1到x2的平均变
化率的定义吗?函数 f (x) 从x1到x2的平均变化率为
习惯上:Δx=x2-x1, Δy=f(x2)-f(x1)
则平均变化率为平均变化率为:思考2:平均变化率有什么几何意义呢? 平均变化率的几何意义就是
函数f(x)图像上两点(x1,f(x1)), (x2,f(x2))所在直线的斜率。 在吹气球的过程中, 可发现,随着气球内空气容量的增加, 气球的半径增加得越来越慢. 从数学的角度, 如何描述这种现象呢?活动1:气球膨胀率试分别求:(1)当空气容积V从0L增加到1L时
(2)当空气容积V从1L增加到2L时
气球的平均膨胀率 可以看出:随着气球体积逐渐变大,它的平均膨胀率逐渐变小了。(1)(2)显然0.62>0.16
思考:当空气的容量从V1增加到V2时,气球的平均膨胀率是多少?活动2 试举出生活中与平均变化率有关的例子。探究:如图是函数h(t)= -4.9t2+6.5t+10的图像,计算运动员在 这段时间里的平均速度,并思考以下问题:
1、运动员在这段时间内是静止的吗?
2、你认为用平均速度描述
运动员的运动状态有什
么问题吗?
(1)[1, 3];
(2)[1, 2];
(3)[1, 1.1];
(4)[1, 1.001];
(5)[1, 1.0001]; 一运动质点的位移S与时间t满足S(t)=t2,分别计算S(t)在下列区间上的平均变化率.(位移单位为m,时间单位为s) 432.12.0011.9991.991.92(6)[0.999, 1];
(7)[0.99, 1];
(8)[0.9, 1].2.0001练一练 如何刻画t=1这一时刻
质点运动的快慢程度呢? 思考:2.我想进一步探究的问题是——1.这节课我的收获是——小结:3.这节课我最感兴趣的地方是——1.必做题2.选做题3.思考题课本第10页习题1.1A组:1 已知函数 ,
求 的值: 一运动质点的位移S与时间t满足S(t)=t2, 如何刻画t=1这一时刻质点运动变化的快慢程度呢? (位移单位为m, 时间单位为s) 作业:谢 谢 大 家! 再见!
