人教版八年级数学上册教学课件《13.3.1 等腰三角形的性质》 (共14张PPT)
文档属性
| 名称 | 人教版八年级数学上册教学课件《13.3.1 等腰三角形的性质》 (共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 935.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-16 23:59:15 | ||
图片预览


文档简介
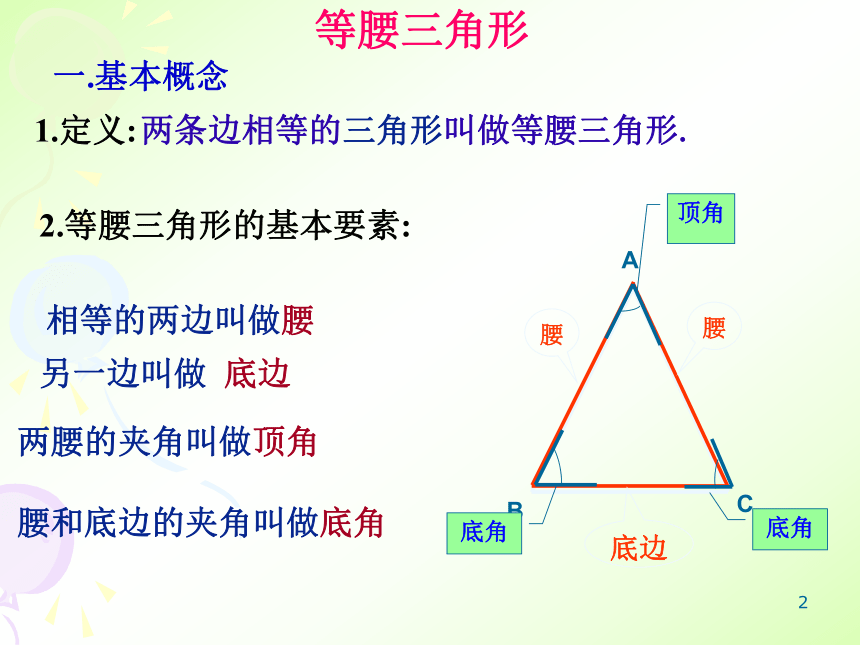
课件14张PPT。等腰三角形的性质13.3.11 等腰三角形一.基本概念 1.定义:两条边相等的三角形叫做等腰三角形. 2.等腰三角形的基本要素:相等的两边叫做腰另一边叫做 底边 两腰的夹角叫做顶角 腰和底边的夹角叫做底角 2腰:
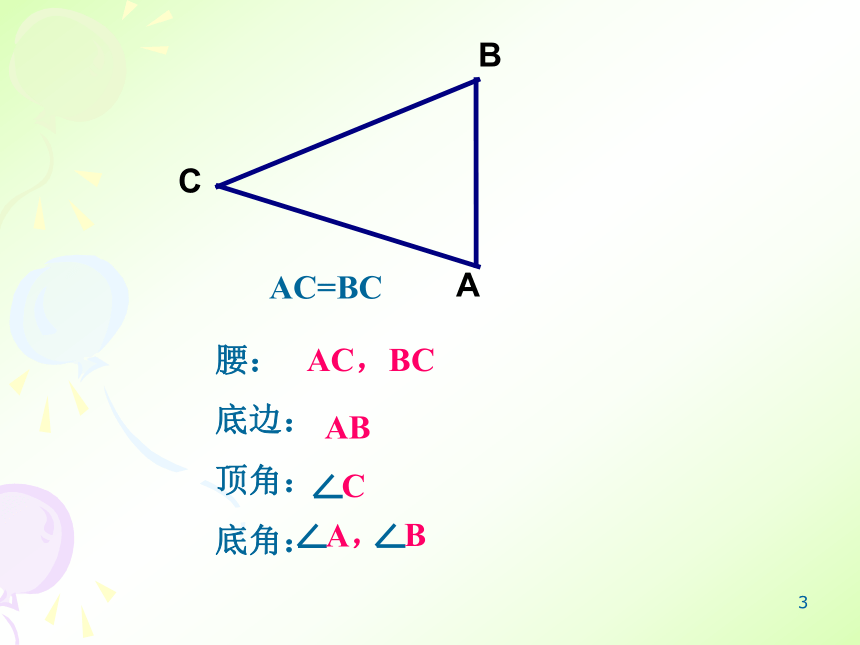
底边:
顶角:
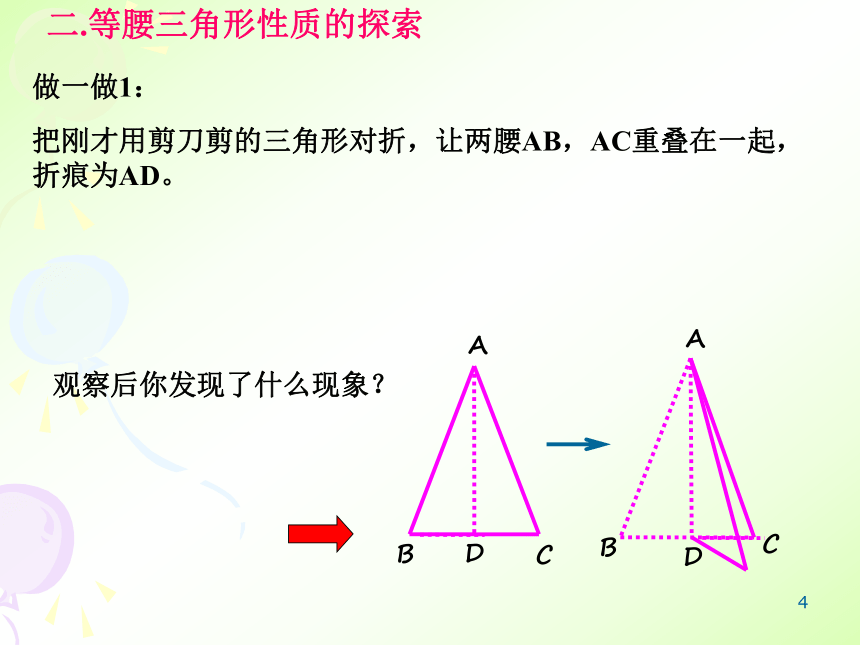
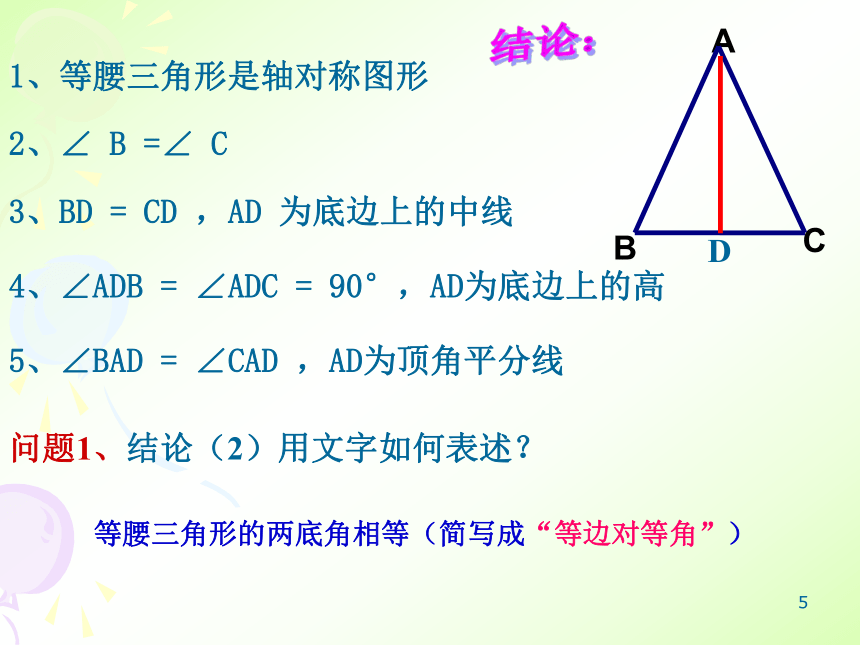
底角:AC,BCAB3做一做1: 把刚才用剪刀剪的三角形对折,让两腰AB,AC重叠在一起,折痕为AD。 观察后你发现了什么现象?二.等腰三角形性质的探索4结论:1、等腰三角形是轴对称图形2、∠ B =∠ C3、BD = CD ,AD 为底边上的中线4、∠ADB = ∠ADC = 90°,AD为底边上的高5、∠BAD = ∠CAD ,AD为顶角平分线问题1、结论(2)用文字如何表述?等腰三角形的两底角相等(简写成“等边对等角”)5(2)要注意是哪三线?等腰三角形底边上的高、中线及顶角的平分线
互相重合。(简称“三线合一”)(1)“等腰三角形”是三线合一的大前提问题2、结论(3)、(4)、(5)用一句话可以归纳
为什么?6D如何证明:等腰三角形的两个底角相等(简写“等边对等角”)已知:如图△ABC中AB=AC求证:∠B=∠C证明:作∠BAC的平分线AD在△ABD和△ACD中AB=AC(已知)AD=AD(公共边)∴ △ABD≌△ACD(SAS)∴∠B=∠C(全等三角形的对应角相等)思考1:还有其他的证明方法吗?思考2:你有办法证明等腰三角形的“三线合一”吗?7∴ ∠BAD=∠CAD ∠BAD=∠CAD等腰三角形的性质1、等腰三角形的两个底角相等。
(简称“等边对等角”)2、等腰三角形底边上的高、中线及顶角的平分线
互相重合(简称“三线合一”)一般的三角形有这种性质吗?要注意是指顶角的平分线、底边上的高、底边上的中线这三线重合。8CDBA①在ΔABC中,∵AB=AC,
∴ ∠B=∠C( )等腰三角形的性质 等边对等角(1)∵AD⊥BC,
∴∠____ = ∠____,___= ___ (2)∵AD是中线,∴___⊥___ ,∠____ =∠____ (3)∵AD是角平分线,∴___ ⊥___ ,___ =___BAD CADBD CD AD BC AD BCBAD CADBD CD②在△ABC中, AB=AC时, 9例1、如图,在△ABC中,AB = AC,D是BC边上的中点,
∠B = 40°,求 ∠1 和 ∠ADC的度数。解: ∵AD是△ABC的中线(已知)
∴∠ADC = ∠ADB= 90°∴∠ 1 =90° - ∠B = 50° ,10∴AD是△ABC底边上的高(三线合一)1.等腰三角形一个角为70°,它的另外两个角为
___________________
2.等腰三角形一个角为110°,它的另外两个角为 ________ 70°,40°或55°,55°35°,35°随堂练习:________2011练习、判断下列命题是否正确。
(1)等腰三角形的角平分线、中线和高互相重合( )
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°。 ( )
(3)等腰三角形的底角都是锐角 ( )
(4)钝角三角形不可能是等腰三角形 ( )
××√√12小结:1、等腰三角形的性质:等边对等角2、等腰三角形的顶角平分线、底边上的中线
和底边上的高互相重合(三线合一) 3、“三线合一”性质在实际应用中,只要推出
其中一个 结论成立,其它两个结论一定成立,
所以关键是寻找其中一个结论成立的条件。本节课你学到了什么?4、等边三角形的性质。13作业P83 练习 2、3、4题14
底边:
顶角:
底角:AC,BCAB3做一做1: 把刚才用剪刀剪的三角形对折,让两腰AB,AC重叠在一起,折痕为AD。 观察后你发现了什么现象?二.等腰三角形性质的探索4结论:1、等腰三角形是轴对称图形2、∠ B =∠ C3、BD = CD ,AD 为底边上的中线4、∠ADB = ∠ADC = 90°,AD为底边上的高5、∠BAD = ∠CAD ,AD为顶角平分线问题1、结论(2)用文字如何表述?等腰三角形的两底角相等(简写成“等边对等角”)5(2)要注意是哪三线?等腰三角形底边上的高、中线及顶角的平分线
互相重合。(简称“三线合一”)(1)“等腰三角形”是三线合一的大前提问题2、结论(3)、(4)、(5)用一句话可以归纳
为什么?6D如何证明:等腰三角形的两个底角相等(简写“等边对等角”)已知:如图△ABC中AB=AC求证:∠B=∠C证明:作∠BAC的平分线AD在△ABD和△ACD中AB=AC(已知)AD=AD(公共边)∴ △ABD≌△ACD(SAS)∴∠B=∠C(全等三角形的对应角相等)思考1:还有其他的证明方法吗?思考2:你有办法证明等腰三角形的“三线合一”吗?7∴ ∠BAD=∠CAD ∠BAD=∠CAD等腰三角形的性质1、等腰三角形的两个底角相等。
(简称“等边对等角”)2、等腰三角形底边上的高、中线及顶角的平分线
互相重合(简称“三线合一”)一般的三角形有这种性质吗?要注意是指顶角的平分线、底边上的高、底边上的中线这三线重合。8CDBA①在ΔABC中,∵AB=AC,
∴ ∠B=∠C( )等腰三角形的性质 等边对等角(1)∵AD⊥BC,
∴∠____ = ∠____,___= ___ (2)∵AD是中线,∴___⊥___ ,∠____ =∠____ (3)∵AD是角平分线,∴___ ⊥___ ,___ =___BAD CADBD CD AD BC AD BCBAD CADBD CD②在△ABC中, AB=AC时, 9例1、如图,在△ABC中,AB = AC,D是BC边上的中点,
∠B = 40°,求 ∠1 和 ∠ADC的度数。解: ∵AD是△ABC的中线(已知)
∴∠ADC = ∠ADB= 90°∴∠ 1 =90° - ∠B = 50° ,10∴AD是△ABC底边上的高(三线合一)1.等腰三角形一个角为70°,它的另外两个角为
___________________
2.等腰三角形一个角为110°,它的另外两个角为 ________ 70°,40°或55°,55°35°,35°随堂练习:________2011练习、判断下列命题是否正确。
(1)等腰三角形的角平分线、中线和高互相重合( )
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°。 ( )
(3)等腰三角形的底角都是锐角 ( )
(4)钝角三角形不可能是等腰三角形 ( )
××√√12小结:1、等腰三角形的性质:等边对等角2、等腰三角形的顶角平分线、底边上的中线
和底边上的高互相重合(三线合一) 3、“三线合一”性质在实际应用中,只要推出
其中一个 结论成立,其它两个结论一定成立,
所以关键是寻找其中一个结论成立的条件。本节课你学到了什么?4、等边三角形的性质。13作业P83 练习 2、3、4题14
