苏科版九年级上册物理14.4 欧姆定律的应用(2)(填空部分专练)(解析版)
文档属性
| 名称 | 苏科版九年级上册物理14.4 欧姆定律的应用(2)(填空部分专练)(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 291.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-11-19 00:00:00 | ||
图片预览

文档简介
14.4
欧姆定律的应用(2)
(填空部分)
1.在串联电路中,若R1:R2=5:2,则通过两个电阻的电流之比是 ,R1与R2两端的电压之比为 .
2.电阻为12Ω的电铃,正常工作时的电压为6V,现只有一个8V的电源,要使它正常工作,要给它 联一个 Ω的电阻.
3.如图所示,当开关S闭合,甲、乙两表均为电压表时,两表示数之比U甲:U乙=3:1;当开关S断开,甲、乙两表均为电流表时,两表示数之比I甲:I乙= ,相同时间内R1、R2产生的热量之比Q1:Q2= .
4.如图所示的电路,电源电压恒定不变,闭合开关S,将滑动变阻器的滑片P自右向左移动的过程中,电压表示数将 ,电流表示数将 (均选填“变大”、“不变”或“变小”).
5.如图所示,电源电压恒为6V,R1的阻值为8Ω,R2两端的电压为4V,则通过b点的电流为 A,R2的阻值为 Ω.
6.某段金属导体两端电压为4V时,通过的电流是0.2A;当该导体两端电压为12V时,通过该导体的电流为 A;当该导体两端电压降为0时,电阻为 Ω.
7.如图所示,电源电压保持6V不变,电阻R1=10Ω,R2=20Ω,闭合开关S,通电30s,则电阻R1产生的热量为 J.
8.图中电源电压保持不变,灯泡标有“6V
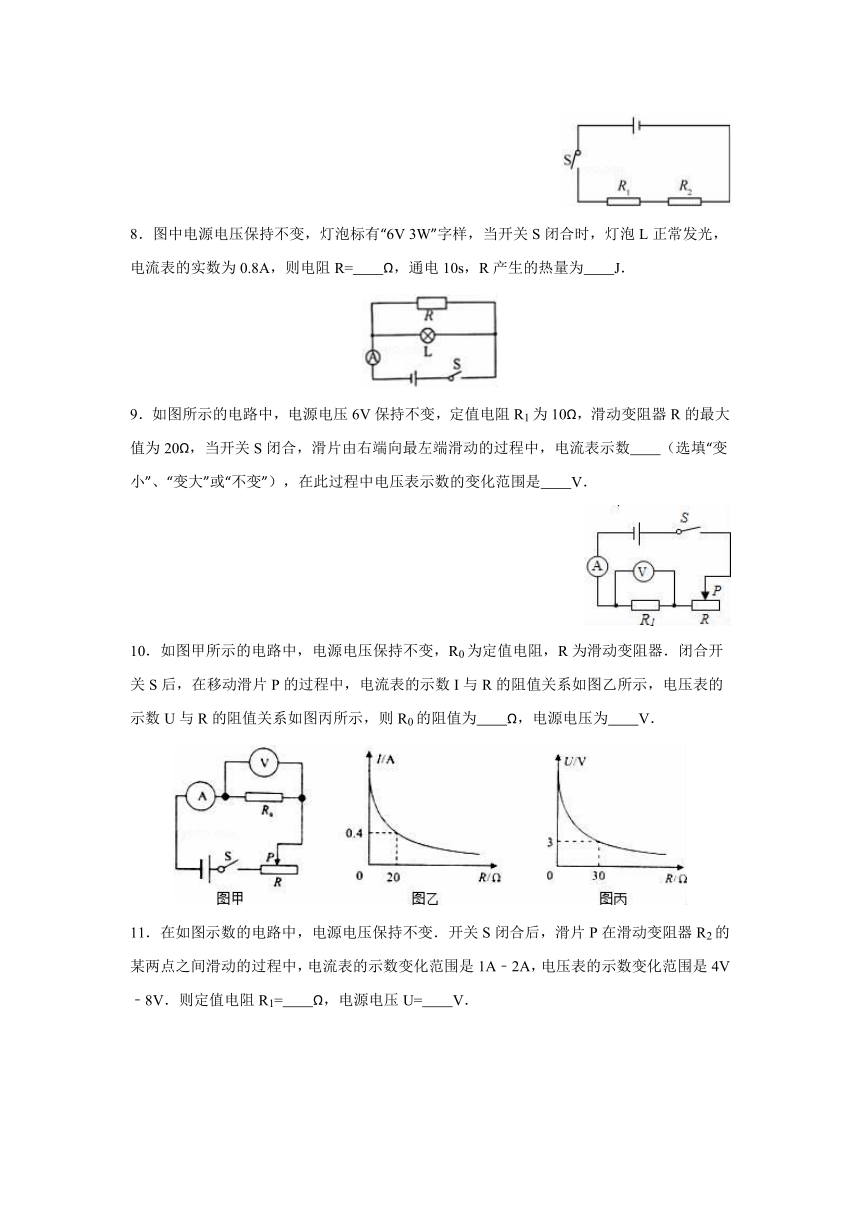
3W”字样,当开关S闭合时,灯泡L正常发光,电流表的实数为0.8A,则电阻R= Ω,通电10s,R产生的热量为 J.
9.如图所示的电路中,电源电压6V保持不变,定值电阻R1为10Ω,滑动变阻器R的最大值为20Ω,当开关S闭合,滑片由右端向最左端滑动的过程中,电流表示数 (选填“变小”、“变大”或“不变”),在此过程中电压表示数的变化范围是 V.
10.如图甲所示的电路中,电源电压保持不变,R0为定值电阻,R为滑动变阻器.闭合开关S后,在移动滑片P的过程中,电流表的示数I与R的阻值关系如图乙所示,电压表的示数U与R的阻值关系如图丙所示,则R0的阻值为 Ω,电源电压为 V.
11.在如图示数的电路中,电源电压保持不变.开关S闭合后,滑片P在滑动变阻器R2的某两点之间滑动的过程中,电流表的示数变化范围是1A﹣2A,电压表的示数变化范围是4V﹣8V.则定值电阻R1= Ω,电源电压U= V.
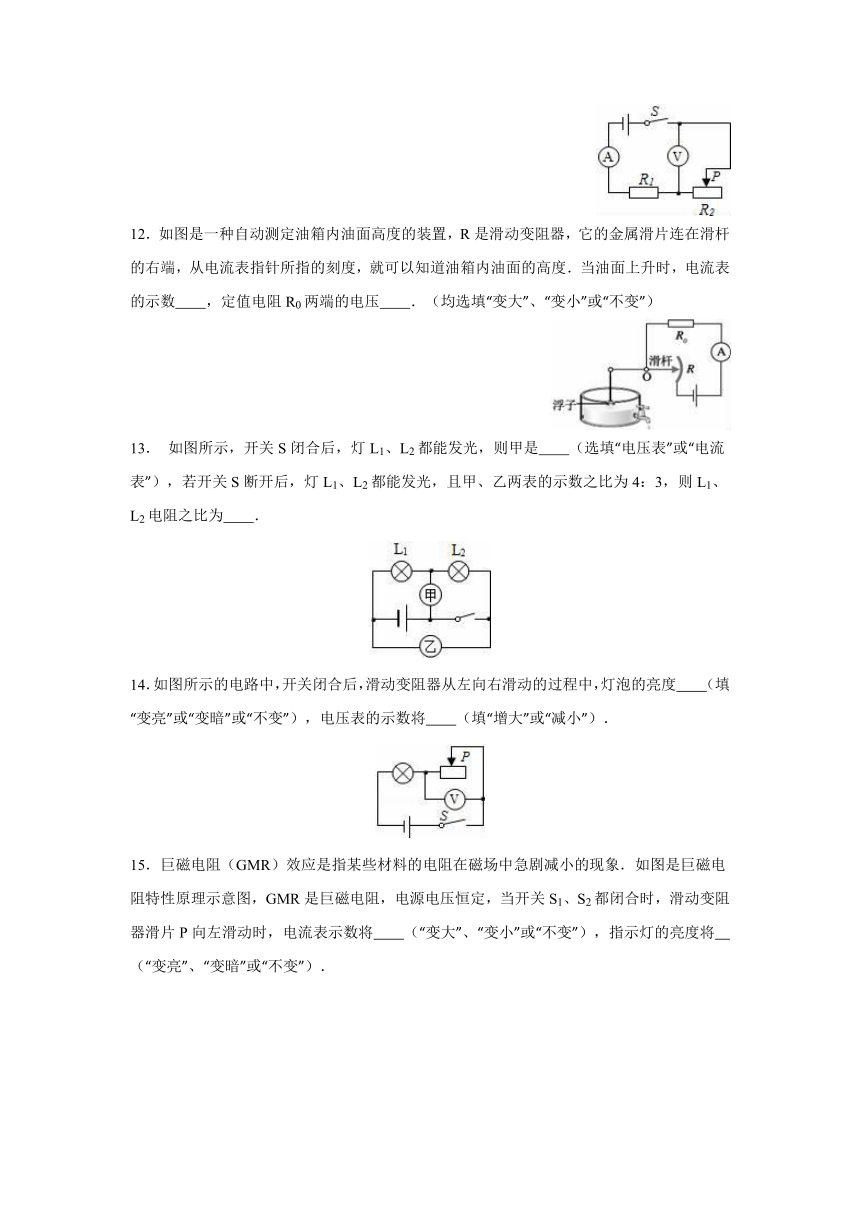
12.如图是一种自动测定油箱内油面高度的装置,R是滑动变阻器,它的金属滑片连在滑杆的右端,从电流表指针所指的刻度,就可以知道油箱内油面的高度.当油面上升时,电流表的示数 ,定值电阻R0两端的电压 .(均选填“变大”、“变小”或“不变”)
13.
如图所示,开关S闭合后,灯L1、L2都能发光,则甲是 (选填“电压表”或“电流表”),若开关S断开后,灯L1、L2都能发光,且甲、乙两表的示数之比为4:3,则L1、L2电阻之比为 .
14.如图所示的电路中,开关闭合后,滑动变阻器从左向右滑动的过程中,灯泡的亮度 (填“变亮”或“变暗”或“不变”),电压表的示数将 (填“增大”或“减小”).
15.巨磁电阻(GMR)效应是指某些材料的电阻在磁场中急剧减小的现象.如图是巨磁电阻特性原理示意图,GMR是巨磁电阻,电源电压恒定,当开关S1、S2都闭合时,滑动变阻器滑片P向左滑动时,电流表示数将 (“变大”、“变小”或“不变”),指示灯的亮度将 (“变亮”、“变暗”或“不变”).
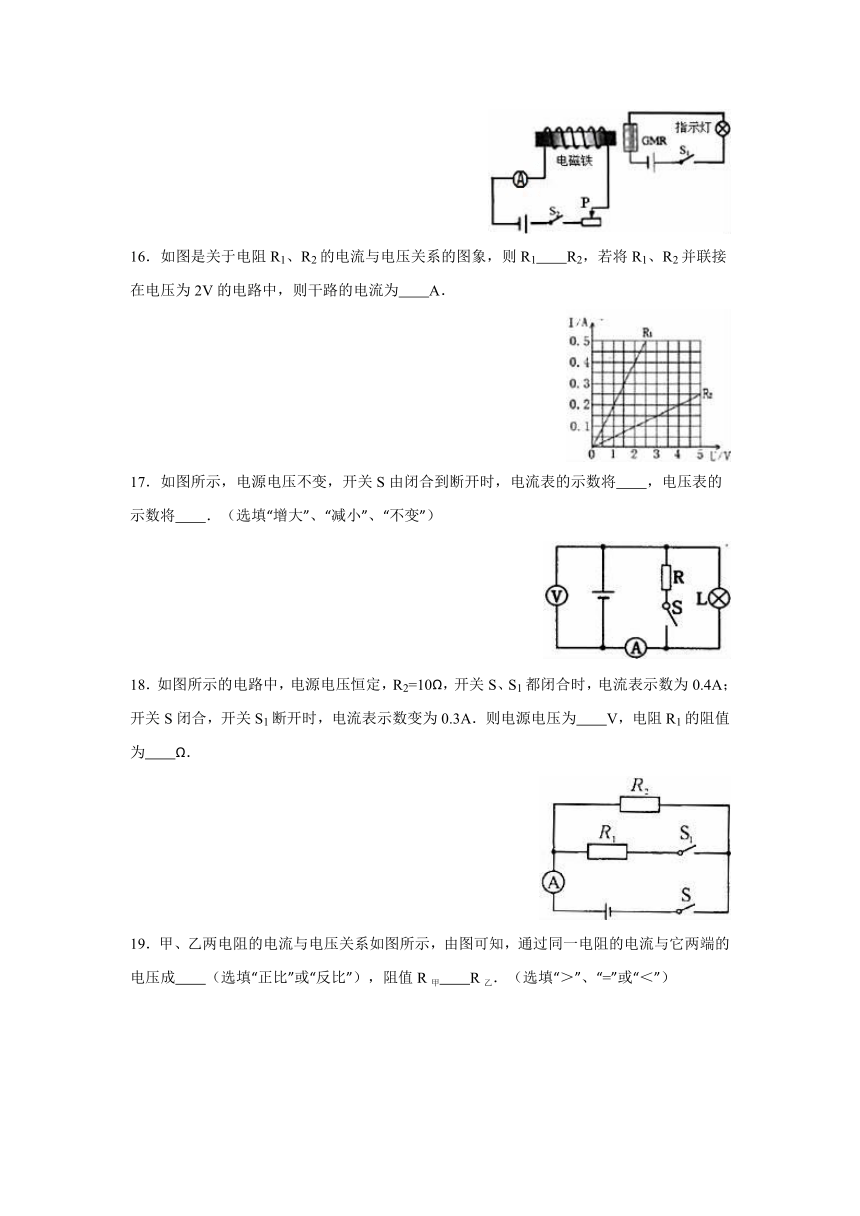
16.如图是关于电阻R1、R2的电流与电压关系的图象,则R1 R2,若将R1、R2并联接在电压为2V的电路中,则干路的电流为 A.
17.如图所示,电源电压不变,开关S由闭合到断开时,电流表的示数将 ,电压表的示数将 .(选填“增大”、“减小”、“不变”)
18.如图所示的电路中,电源电压恒定,R2=10Ω,开关S、S1都闭合时,电流表示数为0.4A;开关S闭合,开关S1断开时,电流表示数变为0.3A.则电源电压为 V,电阻R1的阻值为 Ω.
19.甲、乙两电阻的电流与电压关系如图所示,由图可知,通过同一电阻的电流与它两端的电压成 (选填“正比”或“反比”),阻值R甲 R乙.(选填“>”、“=”或“<”)
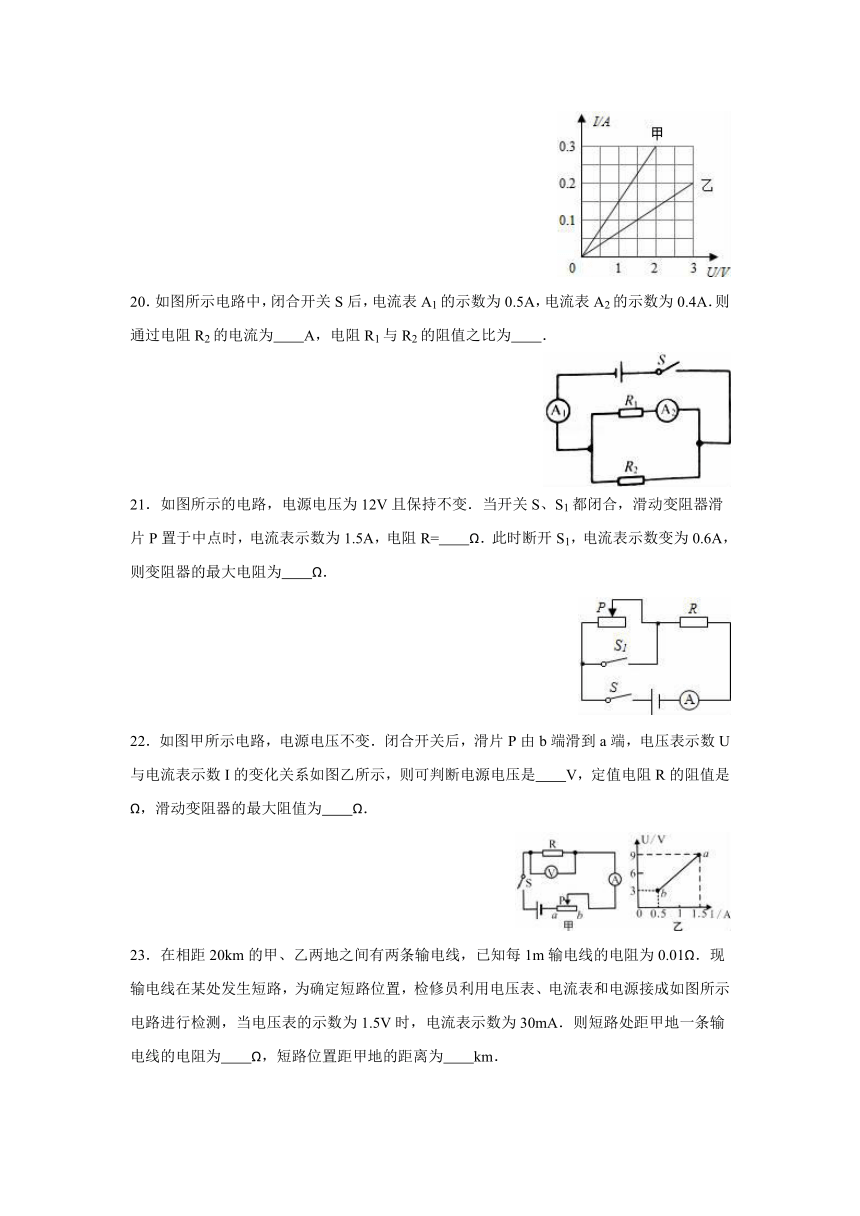
20.如图所示电路中,闭合开关S后,电流表A1的示数为0.5A,电流表A2的示数为0.4A.则通过电阻R2的电流为 A,电阻R1与R2的阻值之比为 .
21.如图所示的电路,电源电压为12V且保持不变.当开关S、S1都闭合,滑动变阻器滑片P置于中点时,电流表示数为1.5A,电阻R= Ω.此时断开S1,电流表示数变为0.6A,则变阻器的最大电阻为 Ω.
22.如图甲所示电路,电源电压不变.闭合开关后,滑片P由b端滑到a端,电压表示数U与电流表示数I的变化关系如图乙所示,则可判断电源电压是 V,定值电阻R的阻值是 Ω,滑动变阻器的最大阻值为 Ω.
23.在相距20km的甲、乙两地之间有两条输电线,已知每1m输电线的电阻为0.01Ω.现输电线在某处发生短路,为确定短路位置,检修员利用电压表、电流表和电源接成如图所示电路进行检测,当电压表的示数为1.5V时,电流表示数为30mA.则短路处距甲地一条输电线的电阻为 Ω,短路位置距甲地的距离为 km.
24.如图所示是一种自动测定油箱内由高度的油量表(是由量程为0~0.6A的电流表改装而成),金属杠杆的右端是滑动变阻器的滑片.从油量表指针所指的刻度,就可以知道油箱内油面的高度.电源电压为12V,定值电阻R0的作用是 ;当油箱油面下降时,油量表的示数将 (选填“增大”、“减小”或“不变”);油箱装满油时,油量表为最大值(即电流表达到最大值,此时滑动变阻器的触头在某一端),则R0
的值是 Ω.
25.
如图是甲、乙两导体的电流与电压关系图象,由图可得乙的电阻是 Ω,若把甲、乙两电阻串联在电路中,加在甲、乙两电阻上的电压之比U甲:U乙= .
26.如图所示电路,灯泡L1、L2、L3分别标有“6V
3W”、“6V
3.6W”、“10V
5W”字样(不考虑温度对灯丝电阻的影响).
(1)只闭合开关S1时,要使其中一只灯泡正常发光,另一只不烧坏,电源最大电压是 V,通电1min灯泡L2产生的热量是 J.
(2)如果电源电压为2.4V,要使电流表示数最大,则应闭合开关 ,电流表示数为 A.
27.如图所示为一种人体秤的工作原理示意图,电源电压恒定不变.体重显示表是由电流表改装而成,定值电阻R0起保护电路作用,其电阻值为10Ω,在人体秤上不施加力时滑片P在电阻R的最上端,施加的力最大时滑片P移至电阻R的最下端,该人体秤测量范围0~100kg,电路中电流变化范围0.1~0.6A,则电源电压为 V,滑动变阻器的最大值为 Ω.
28.如图所示,电源电压不变,R1=2Ω,R2=3Ω,R3=4Ω.只闭合S,电流表A1、A2示数之比为 ,电压表V1、V2示数之比为 .再闭合S1、S2,电流表A1、A2示数之比为 ,电压表V1、V2示数之比为 .
29.小英按图甲所示的电路图连接实验电路,测量电阻Rx的阻值.闭合开关S,调节滑动变阻器的滑片P后,观察到电压表和电流表的示数分别如图乙、丙所示,则电压表的示数为 V,电流表的示数为 A,待测电阻Rx的阻值为 Ω.
30.如图所示,电阻R1标有“6Ω
lA”,R2标有“3Ω
1.2A”,电流表A1、A2的量程均为0~3A,电压表量程0~15V,在a、b间接入电压可调的直流电源.闭合开关s后,为保证R1、R2均不损坏,则允许加的最大电源电压是 ,通过电流表A1的电流不得超过 .
参考答案与解析
1.在串联电路中,若R1:R2=5:2,则通过两个电阻的电流之比是 1:1 ,R1与R2两端的电压之比为 5:2 .
【分析】根据串联电路的电流关系、电压关系求解
【解答】解:∵两个电阻串联
∴I1=I2,即:I1:I2=1:1,
∴U1:U2=R1:R2=5:2
故答案为:1:1,5:2
【点评】灵活运用串联电路的特点(I=I1=I2、U=U1+U2、R=R1+R2)及分压关系
2.电阻为12Ω的电铃,正常工作时的电压为6V,现只有一个8V的电源,要使它正常工作,要给它 串 联一个 4 Ω的电阻.
【分析】比较电铃的电压与电源电压,可知电源电压大于电铃的额定电压,故需要串联一个电阻分压,串联电阻两端的电压等于电源电压减去电铃的额定电压;
因为电铃正常工作,电铃两端的电压等于额定电压,已知电铃的电阻,则利用欧姆定律求此时通过电铃的电流,则串联电阻的阻值利用R=计算.
【解答】解:要使电铃正常工作,需要给电铃串联一个电阻R,串联电阻R两端的电压:
UR=U﹣U额=8V﹣6V=2V,
∵电铃正常工作,
I===0.5A;
则串联电阻R===4Ω;
故答案为:串,4.
【点评】本题考查了学生对欧姆定律、电阻串联特点的掌握和运用,应熟练掌握相关内容并能灵活应用.
3.如图所示,当开关S闭合,甲、乙两表均为电压表时,两表示数之比U甲:U乙=3:1;当开关S断开,甲、乙两表均为电流表时,两表示数之比I甲:I乙= 2:3 ,相同时间内R1、R2产生的热量之比Q1:Q2= 1:2 .
【分析】(1)当开关S闭合,甲、乙两表为电压表时,两电阻串联,甲测电源的电压,乙测R2两端的电压;根据串联电路的电流特点和欧姆定律得出两电阻的阻值之比;
(2)当开关S断开,甲、乙两表为电流表时,两电阻并联,甲测通过R2的电流,乙测干路电流;根据并联电路的电压特点求出通过两支路的电流之比,根据并联电路的电流特点求出两电流表示数的比值;根据并联电路的电压特点和Q=W=求出R1、R2产生的热量之比.
【解答】解:当开关S闭合,甲、乙两表为电压表时,等效电路图如下图所示:
由于串联电路各处的电流相等,根据U=IR可知,
两电压表的示数之比:
====,
解得:
=;
当开关S断开,甲、乙两表为电流表时,等效电路图如下图所示:
由于并联电路各支路两端的电压相等,根据I=可知,
R1和R2的电流之比:
==,
两电流表的示数之比:
===,
由Q=W=t可知,相同时间内R1、R2产生的热量之比:
==.
故答案为:2:3;1:2.
【点评】本题关键有二:一画等效电路图,二理清串联电路的分压关系(U1:U2=R1:R2)和并联电路的电流、电功率的关系(P1:P2=I1:I2=R2:R1)
4.如图所示的电路,电源电压恒定不变,闭合开关S,将滑动变阻器的滑片P自右向左移动的过程中,电压表示数将 变大 ,电流表示数将 不变 (均选填“变大”、“不变”或“变小”).
【分析】由电路图可知,灯泡与滑动变阻器串联,滑动变阻器完全接入电路中,电流表测电路电流,电压表测量滑动变阻器滑片右侧接入电路的电阻两端的电压;
由滑动变阻器滑片方向变化得出滑动变阻器滑片右侧接入电路的电阻阻值变化,从而得出电压表和电流表示数的比值变化.
【解答】解:由电路图可知,灯泡与滑动变阻器串联,滑动变阻器完全接入电路中,电流表测电路中的电流,电压表测量滑动变阻器滑片右侧接入电路的电阻两端的电压;
由于滑动变阻器的电阻全部连入电路,则在滑动变阻器的滑片P自右向左移动的过程中,电路中的总电阻不变,根据欧姆定律可知电路中的电流不变,即电流表示数不变;
由于变阻器滑片右侧接入电路的电阻阻值变大,根据U=IR可知电压表示数变大.
故答案为:变大;不变.
【点评】本题考查了电压表和电流表示数的比值的变化,分析清楚电路结构,明确电压表与电流表所测的量,熟练应用欧姆定律是正确解题的关键.
5.如图所示,电源电压恒为6V,R1的阻值为8Ω,R2两端的电压为4V,则通过b点的电流为 0.25 A,R2的阻值为 16 Ω.
【分析】由电路图可知,R1与R2串联,根据串联电路的电压特点求出电阻R1两端的电压;根据欧姆定律和串联电路的电流特点求出电路中的电流,再根据欧姆定律求出电阻R2的阻值.
【解答】解:由电路图可知,R1与R2串联.
因串联电路中总电压等于各分电压之和,
所以,电阻R1两端的电压:
U1=U﹣U2=6V﹣4V=2V;
因串联电路中各处的电流相等,
所以,通过b点的电流:
Ib=I2=I1===0.25A,
由I=得电阻R2的阻值:
R2===16Ω.
故答案为:0.25;16.
【点评】本题考查了串联电路的特点和欧姆定律的应用,是一道较为简单的应用题.
6.某段金属导体两端电压为4V时,通过的电流是0.2A;当该导体两端电压为12V时,通过该导体的电流为 0.6 A;当该导体两端电压降为0时,电阻为 20 Ω.
【分析】(1)知道导体两端的电压和通过的电流,根据欧姆定律求出导体的电阻;
(2)电阻是导体本身的一种性质,只与导体的材料、长度、横截面积和温度有关,与两端的电压和通过的电流无关,再根据欧姆定律求出当该导体两端电压为12V时通过该导体的电流.
【解答】解:由I=可得,导体的电阻:
R===20Ω,
因电阻是导体本身的一种性质,与两端的电压和通过的电流无关,
所以,当该导体两端电压为12V时或该导体两端电压降为0时,导体的电阻仍为20Ω不变,
当该导体两端电压为12V时,通过该导体的电流:
I′===0.6A.
故答案为:0.6;20.
【点评】本题考查了欧姆定律的简单应用,关键是知道导体的电阻与两端的电压和通过的电流无关,是一道基础题目.
7.如图所示,电源电压保持6V不变,电阻R1=10Ω,R2=20Ω,闭合开关S,通电30s,则电阻R1产生的热量为 12 J.
【分析】根据电阻的串联和欧姆定律求出电路中的电流的电流,再根据Q=I2Rt求出通电30s电阻R1产生的热量.
【解答】解:因串联电路中总电阻等于各分电阻之和,
所以,电路中的电流:
I===0.2A,
则通电30s电阻R1产生的热量:
Q1=I2R1t=(0.2A)2×10Ω×30s=12J.
故答案为:12.
【点评】本题考查了电阻的串联和欧姆定律、焦耳定律的应用,是一道基础题目.
8.图中电源电压保持不变,灯泡标有“6V
3W”字样,当开关S闭合时,灯泡L正常发光,电流表的实数为0.8A,则电阻R= 20 Ω,通电10s,R产生的热量为 18 J.
【分析】因为灯泡和电阻并联,根据P=UI求出灯泡中的电流,再并联电路的电流特点求出电阻中的电流,根据欧姆定律即可求出电阻R的阻值,根据Q=W=UIt求出电阻产生的热量.
【解答】解:当闭合开关S时,灯L正常发光,说明电源电压为U=6V,电流表测的是总电流,则I=0.8A,
由P=UI可知:
灯泡中的电流IL===0.5A,
根据并联电路的干路电流等于各支路电流之和可知:
电阻中的电流IR=I﹣IL=0.8A﹣0.5A=0.3A,
由I=得:
电阻R===20Ω;
通电1min电阻R产生的热量:
Q=W=UIRt=6V×0.3A×10s=18J.
故答案为:20;18.
【点评】本题考查并联电路的特点和欧姆定律、焦耳定律公式的理解和掌握,弄明白电压和电流关系是解决此题的关键.
9.如图所示的电路中,电源电压6V保持不变,定值电阻R1为10Ω,滑动变阻器R的最大值为20Ω,当开关S闭合,滑片由右端向最左端滑动的过程中,电流表示数 变大 (选填“变小”、“变大”或“不变”),在此过程中电压表示数的变化范围是 2V~6 V.
【分析】由电路图可知,定值电阻R1与滑动变阻器R串联,电压表测定值电阻两端的电压,电流表测电路中的电流.
(1)根据滑片的移动可知接入电路中电阻的变化,根据欧姆定律可知电路中电流的变化;
(2)当滑片位于左端时,电路为定值电阻的简单电路,电压表测电源的电压示数最大;当滑片位于右端时,接入电路中的电阻最大,电路中的电流最小,电压表的示数最小,根据电阻的串联和欧姆定律求出电路中的电流,再利于欧姆定律求出电压表的最小示数,然后得出答案.
【解答】解:由电路图可知,定值电阻R1与滑动变阻器R串联,电压表测定值电阻两端的电压,电流表测电路中的电流.
(1)当开关S闭合,滑片由右端向最左端滑动的过程中,接入电路中电阻变小,电路中的总电阻变小,
由I=可知,电路中的电路变大,即电流表的示数变大;
(2)当滑片位于右端时,接入电路中的电阻最大,电路中的电流最小,电压表的示数最小,
因串联电路中总电阻等于各分电压之和,
所以,电路中的最小电流:
I===0.2A,
电压表的最小示数:
U1=IR1=0.2A×10Ω=2V,
当滑片位于左端时,电路为定值电阻的简单电路,电压表测电源的电压,则电压表的最大示数为6V;
所以,在此过程中电压表示数的变化范围为2V~6V.
故答案为:变大;2V~6.
【点评】本题考查了电路的动态分析和串联电路特点以及欧姆定律的应用,要注意滑动变阻器接入电路中的电阻最大时电路中的电流最小.
10.如图甲所示的电路中,电源电压保持不变,R0为定值电阻,R为滑动变阻器.闭合开关S后,在移动滑片P的过程中,电流表的示数I与R的阻值关系如图乙所示,电压表的示数U与R的阻值关系如图丙所示,则R0的阻值为 10 Ω,电源电压为 12 V.
【分析】由电路图可知,R与R0串联,电压表测R0两端的电压,电流表测电路中的电流.由图乙可知,滑动变阻器接入电路中的阻值为20Ω时电路中的电流,根据电阻的串联和欧姆定律表示出电源的电压,根据图丙可知滑动变阻器接入电路中的电阻为30Ω时电压表的示数,根据串联电路的电流特点和欧姆定律表示出电路中的电流,根据电阻的串联和欧姆定律表示出电源的电压,利用电源的电压不变得出方程,解方程求出R0的阻值,进一步求出电源的电压.
【解答】解:由电路图可知,R与R0串联,电压表测R0两端的电压,电流表测电路中的电流.
由图乙可知,滑动变阻器接入电路中的阻值R1=20Ω时,电路中的电流I1=0.4A,
因串联电路中总电阻等于各分电阻之和,
所以,由I=可得,电源的电压:
U=I1(R0+R1)=0.4A×(R0+20Ω),
由图丙可知,滑动变阻器接入电路中的电阻R2=30Ω时,电压表的示数U0=3V,
因串联电路中各处的电流相等,
所以,电路中的电流:
I2==,
电源的电压:
U=I2(R0+R2)=×(R0+30Ω),
因电源的电压不变,
所以,0.4A×(R0+20Ω)=×(R0+30Ω),
整理可得:0.4R02+5Ω×R0﹣90Ω=0,
解得:R0=10Ω,R0=﹣22.5Ω舍去,
电源的电压U=I1(R0+R1)=0.4A×(10Ω+20Ω)=12V.
故答案为:10;12.
【点评】本题考查了串联电路的特点和欧姆定律的应用,从图象中获取滑动变阻器接入电路中的电阻与对应的电流、电压表的示数是关键.
11.在如图示数的电路中,电源电压保持不变.开关S闭合后,滑片P在滑动变阻器R2的某两点之间滑动的过程中,电流表的示数变化范围是1A﹣2A,电压表的示数变化范围是4V﹣8V.则定值电阻R1= 4 Ω,电源电压U= 12 V.
【分析】由电路图可知,电阻R1与滑动变阻器串联,电压表测滑动变阻器两端的电压,电流表测电路中的电流;
当滑片向左移动时接入电路中的电阻变小,电路中的电流变大,滑动变阻器两端的电压变小,据此得出两电表对应的示数关系;根据串联电路的特点和欧姆定律表示出电源的电压,利用电源的电压不变建立等式即可求出R1的阻值和电源的电压.
【解答】解:当电路中的电流为1A时,电压表的示数为8V,
串联电路中各处的电流相等,且总电压等于各分电压之和,
电源的电压:U=I1R1+U滑=1A×R1+8V﹣﹣①
当电路中的电流为2A时,电压表的示数为4V,
电源的电压:
U=I2R1+U滑′=2A×R1+4V﹣﹣②
又因为电源的电压不变,
所以:1A×R1+8V=2A×R1+4V,
解得:R1=4Ω,
电源的电压U=2A×R0+4V=2A×4Ω+4V=12V.
故答案为:4;12.
【点评】本题考查了串联电路的特点和欧姆定律的应用,关键是滑片移动时电压表和电流表示数对应关系的判断.
12.如图是一种自动测定油箱内油面高度的装置,R是滑动变阻器,它的金属滑片连在滑杆的右端,从电流表指针所指的刻度,就可以知道油箱内油面的高度.当油面上升时,电流表的示数 变大 ,定值电阻R0两端的电压 变大 .(均选填“变大”、“变小”或“不变”)
【分析】由电路图可知,R与R0串联,电流表测电路中的电流,根据油面的变化可知浮子位置的变化和指针移到的方向,进一步可知接入电路中电阻的变化,根据欧姆定律可知电路中电流的变化和定值电阻R0两端的电压变化.
【解答】解:由电路图可知,R与R0串联,电流表测电路中的电流,
当油面上升时,浮子上移,指针下移,R的阻值变小,电路中的总电阻变小,
由I=可知,电路中的电流变大,即电流表的示数变大,
由U=IR可知,定值电阻R0两端的电压变大.
故答案为:变大;变大.
【点评】本题考查了电路的动态分析,涉及到滑动变阻器和欧姆定律的应用,分析好油面变化时R阻值的变化是关键.
13.
如图所示,开关S闭合后,灯L1、L2都能发光,则甲是 电压表 (选填“电压表”或“电流表”),若开关S断开后,灯L1、L2都能发光,且甲、乙两表的示数之比为4:3,则L1、L2电阻之比为 3:1 .
【分析】(1)开关S闭合后,灯L1、L2都能发光,根据电压表相当于开路,电流表相当于导线即可判断甲乙表的类型.
(2)当S断开时,两表全是电流表两灯泡才能发光,并且两电灯并联,甲表测总电流,乙表测流过L2的电流,则由欧姆定律可求得两电阻之比;
【解答】解:(1)开关S闭合后,甲乙表必须是相当于开路的电压表,这样电流才能通过灯泡L2、L1,灯L1、L2都能发光.
(2)当S断开时,甲乙表必须是相当于导线的电流表,两灯泡才能发光,并且两电灯并联,甲表测总电流,乙表测流过L2的电流,
已知甲、乙两表的示数之比为4:3,设甲表中电流为I甲=4I,则乙表中电流为I2=I乙=3I,
则由并联电路的电流特点可知,流过R1中的电流I1=I甲﹣I乙=4I﹣3I=I;
由欧姆定律I=可得:
====.
故答案为:电压表;3:1.
【点评】本题考查电压表和电流表的使用特点和串并联电路的特点,在电路中电流表可看成是导线没有电阻,而电压表则看作是断路,则可以明确电路的结构.
14.如图所示的电路中,开关闭合后,滑动变阻器从左向右滑动的过程中,灯泡的亮度 变暗 (填“变亮”或“变暗”或“不变”),电压表的示数将 增大 (填“增大”或“减小”).
【分析】由电路图可知,灯泡与滑动变阻器串联,滑动变阻器从左向右滑动的过程中阻值变大,电路中的电流变小,小灯泡两端的电压变小,其功率变小,故亮度变暗,根据滑动变阻器滑片移动方向判断滑动变阻器接入电路的电阻如何变化,由串联电路的特点判断电压表示数如何变化.
【解答】解:由电路图分析可知,灯泡与滑动变阻器串联;
开关闭合后,滑动变阻器从左向右滑动的过程中,变阻器接入电路的阻值变大,电路中的电阻变大,电流变小,小灯泡两端的电压变小,由P=UI可知灯的电功率变小,故其亮度变暗.
由于电压表测量的是滑动变阻器的电压,滑片P从左向右滑动时,滑动变阻器接入电路的阻值变大,根据串联分压知识可知,滑动变阻器两端的电压变大,即电压表示数变大.
故答案为:变暗;增大.
【点评】本题是一道动态分析题,是常考题型,要掌握这类题的解题思路;分析清楚电路结构、熟练应用串联电路特点及欧姆定律、电功率公式是正确解题的关键.
15.巨磁电阻(GMR)效应是指某些材料的电阻在磁场中急剧减小的现象.如图是巨磁电阻特性原理示意图,GMR是巨磁电阻,电源电压恒定,当开关S1、S2都闭合时,滑动变阻器滑片P向左滑动时,电流表示数将 变大 (“变大”、“变小”或“不变”),指示灯的亮度将 变亮 (“变亮”、“变暗”或“不变”).
【分析】(1)由左图可知,滑动变阻器的滑片P向左滑动过程中接入电路中电阻的变化,根据欧姆定律可知电路中电流的变化,进一步根据影响电磁铁磁场的因素可知其磁场变化,据此可知右图巨磁电阻的变化;
(2)由右图可知,巨磁电阻和灯泡串联,先判断巨磁电阻的变化,根据欧姆定律可知电路中电流的变化,根据P=I2R可知灯泡实际功率的变化,进一步判断亮暗的变化.
【解答】解:
由左图可知,滑动变阻器的滑片P向左滑动过程中接入电路中电阻变小,总电阻减小
电源电压恒定,由I=可知,电路中的电流变大,即电流表示数变大;
因电磁铁磁性的强弱与线圈匝数和通过的电流有关,且匝数不变,通过的电流越大,磁性越强,所以,此时电磁铁的磁性变强;
由右图可知,巨磁电阻和灯泡串联,
因为巨磁电阻在磁场中急剧减小,所以此时巨磁电阻的阻值会变小,电路中的总电阻变小,
由I=可知,可知电路中的电流变大,通过灯泡的电流变大,
因为P=I2R且灯泡的亮暗取决于实际功率的大小,所以,灯泡的实际功率变大,灯泡变亮.
故答案为:变大;变亮.
【点评】本题考查了电路的动态分析,涉及到电磁铁磁性与电流的关系和电功率公式的应用等,判断出巨磁电阻的变化是解题的关键.
16.如图是关于电阻R1、R2的电流与电压关系的图象,则R1 < R2,若将R1、R2并联接在电压为2V的电路中,则干路的电流为 0.5 A.
【分析】将R1、R2并联接在电压为2V的电路中,它们两端的电压相等,根据图象读出通过两电阻的电流,根据欧姆定律比较两电阻的阻值关系,根据并联电路的电流特点求出干路的电流.
【解答】解:将R1、R2并联接在电压为2V的电路中,
因并联电路中各支路两端的电压相等,
所以,两电阻两端的电压均为2V,
由图象可知,通过两电阻的电流分别为I1=0.4A,I2=0.1A,
由I=的变形式R=可知,R1<R2,
因并联电路中干路电流等于各支路电流之和,
所以,干路的电流:
I=I1+I2=0.4A+0.1A=0.5A.
故答案为:<;0.5.
【点评】本题考查了并联电路的特点和欧姆定律的应用,从图象中获取有用的信息是关键.
17.如图所示,电源电压不变,开关S由闭合到断开时,电流表的示数将 减小 ,电压表的示数将 不变 .(选填“增大”、“减小”、“不变”)
【分析】由图知,S闭合时R与L并联,电流表测干路电流,电压表测电源电压;S断开时,只有L连入电路中.由此根据并联电路特点分析判断电表示数变化情况.
【解答】解:
由图知,电压表测电源电压,且电源电压不变,所以开关S由闭合到断开时,电压表的示数将不变;
S闭合时,R与L并联,电流表测干路电流,干路电流等于R与L的电流之和;
S断开时,只有L连入电路中,电流表测L支路的电流;
因为并联电路各支路互不影响,所以S断开后通过L的电流不变,
由于L支路的电流小于干路电流,所以电流表示数减小.
故答案为:减小;不变.
【点评】本题考查了并联电路电流和电压特点的认识和理解,关键是正确分析开关在不同状态下电路的结构.
18.如图所示的电路中,电源电压恒定,R2=10Ω,开关S、S1都闭合时,电流表示数为0.4A;开关S闭合,开关S1断开时,电流表示数变为0.3A.则电源电压为 3 V,电阻R1的阻值为 30 Ω.
【分析】由电路图可知,开关S、S1都闭合时,R1与R2并联,电流表测干路电流;开关S闭合,开关S1断开时,电路为R2的简单电路,电流表测通过R2的电流,根据并联电路中各支路独立工作、互不影响可知通过R2的电流不变,即此时电流表的示数为通过R2的电流,根据欧姆定律求出电源的电压,根据并联电路的电流特点求出通过R1的电流,利用并联电路的电压特点和欧姆定律求出电阻R1的阻值.
【解答】解:由电路图可知,开关S、S1都闭合时,R1与R2并联,电流表测干路电流;
开关S闭合,开关S1断开时,电路为R2的简单电路,电流表测通过R2的电流,
因并联电路中各支路独立工作、互不影响,
所以,通过R2的电流不变,即通过R2的电流I2=0.3A,
由I=可得,电源的电压:
U=I2R2=0.3A×10Ω=3V,
因并联电路中干路电流等于各支路电流之和,
所以,通过R1的电流:
I1=I﹣I2=0.4A﹣0.3A=0.1A,
因并联电路中各支路两端的电压相等,
所以,电阻R1的阻值:
R1===30Ω.
故答案为:3;30.
【点评】本题考查了并联电路的特点和欧姆定律的应用,要注意“并联电路中各支路独立工作、互不影响”特点的应用.
19.甲、乙两电阻的电流与电压关系如图所示,由图可知,通过同一电阻的电流与它两端的电压成 正比 (选填“正比”或“反比”),阻值R甲 < R乙.(选填“>”、“=”或“<”)
【分析】通过读电流与电压关系图象,可判断二者的关系,根据欧姆定律可判断两者阻值的大小关系.
【解答】解:由图可知,电流与电压的变化图象中,都是过原点的斜向上的直线,所以说明通过同一电阻的电流与它两端的电压成正比;
从图象中数据可以看出,当电压一定时,通过甲电阻的电流大,由欧姆定律R=可得,
甲的阻值小于乙的阻值,即R甲<R乙.
故答案为:正比;<.
【点评】本题解答的关键是要学会读取图象,能从中找出正确的信息,并能熟练运用欧姆定律进行分析和判断.
20.如图所示电路中,闭合开关S后,电流表A1的示数为0.5A,电流表A2的示数为0.4A.则通过电阻R2的电流为 0.1 A,电阻R1与R2的阻值之比为 1:4 .
【分析】由电路图可知,电阻R1与R2并联,电流表A1测干路电流,电流表A2测R1电支路的电流,根据并联电路的电流特点求出通过电阻R2的电流,根据并联电路的电压特点和欧姆定律求出电阻R1与R2的阻值之比.
【解答】解:由电路图可知,电阻R1与R2并联,电流表A1测干路电流,电流表A2测R1电支路的电流,
因并联电路中干路电流等于各支路电流之和,
所以,通过电阻R2的电流:
I2=I﹣I1=0.5A﹣0.4A=0.1A,
因并联电路中各支路两端的电压相等,
所以,由I=可得,电阻R1与R2的阻值之比:
====.
故答案为:0.1;1:4.
【点评】本题考查了并联电路的特点和欧姆定律的应用,计算过程要注意各量之间的关系,不要颠倒.
21.如图所示的电路,电源电压为12V且保持不变.当开关S、S1都闭合,滑动变阻器滑片P置于中点时,电流表示数为1.5A,电阻R= 8 Ω.此时断开S1,电流表示数变为0.6A,则变阻器的最大电阻为 24 Ω.
【分析】当开关S、S1都闭合时,滑动变阻器被短路,电路为R的基本电路,电流表测量电路电流,根据欧姆定律的应用即可求出电阻R的阻值;当断开S1后,滑动变阻器与定值电阻串联,电流表测量电路电流,根据欧姆定律的应用求出电路总电阻,根据串联电路电阻规律求出滑动变阻器接入电路的阻值,再根据滑片位于中点可知滑动变阻器的最大阻值.
【解答】解:当开关S、S1都闭合时,滑动变阻器被短路,电路为R的基本电路,电流表测量电路电流;
由I=可知,电阻R===8Ω;
当断开S1后,滑动变阻器与定值电阻串联,电流表测量电路电流;
由I=可知,电路的总电阻:R总===20Ω;
因为串联电路的总电阻等于各部分电阻之和,
所以滑动变阻器接入电路的阻值:R滑=R总﹣R=20Ω﹣8Ω=12Ω;
由于此时滑片在变阻器的中点处,
所以滑动变阻器的最大电阻:R滑大=2R滑=2×12Ω=24Ω.
故答案为:8;24.
【点评】本题考查串联电路的特点以及欧姆定律的应用,关键明确在开关处于不同状态时电路的连接方式.
22.如图甲所示电路,电源电压不变.闭合开关后,滑片P由b端滑到a端,电压表示数U与电流表示数I的变化关系如图乙所示,则可判断电源电压是 9 V,定值电阻R的阻值是 6 Ω,滑动变阻器的最大阻值为 12 Ω.
【分析】由电路图可知,R与滑动变阻器串联,电压表测R两端的电压,电流表测电路中的电流.
(1)当滑片在a端时,电路为R的简单电路,此时电路中的电流最大,电压表的示数就是电源电压,由图乙读出对应的电流和电压,根据欧姆定律求出定值电阻R阻值;
(2)当滑片位于b端时,R与滑动变阻器的最大阻值串联,此时电路中的电流最小,电压表的示数最小,根据图象读出电表示数,根据串联电路的电压特点求出变阻器两端的电压,利用欧姆定律求出滑动变阻器的最大阻值.
【解答】解:(1)当滑片在a端时,电路为R的简单电路,电压表的示数最大,电流表的示数最小,
由图象可知,电源的电压U=9V,电路中的电流I=1.5A,
由I=可知,电阻R的阻值:
R===6Ω;
(2)当滑片位于b端时,R与滑动变阻器的最大阻值串联,此时电路中的电流最小,电压表的示数最大,
由图象可知,R两端的电压UR=3V,电路中的最小电流I′=0.5A,
因串联电路中总电压等于各分电压之和,
所以,滑动变阻器两端的电压:
U滑=U﹣UR=9V﹣3V=6V,
滑动变阻器的最大阻值:
R滑===12Ω.
故答案为:9;6;12.
【点评】本题结合图象考查了串联电路的特点和欧姆定律的应用,关键是明白滑片移动过程中电路的变化情况,应用图象解决问题,这是以后学习的重点.
23.在相距20km的甲、乙两地之间有两条输电线,已知每1m输电线的电阻为0.01Ω.现输电线在某处发生短路,为确定短路位置,检修员利用电压表、电流表和电源接成如图所示电路进行检测,当电压表的示数为1.5V时,电流表示数为30mA.则短路处距甲地一条输电线的电阻为 25 Ω,短路位置距甲地的距离为 2.5 km.
【分析】(1)知道电压表和电流表的示数,利用欧姆定律求出连接短路位置到甲地的两段输电线的电阻值;
(2)已知1m导线的电阻值,然后让总电阻除以一米导线的电阻即可求出导线的长度,从而确定出短路的地点离甲地的距离.
【解答】解:(1)由I=可知,连接短路位置到甲地的两段输电线的电阻值:R===50Ω;
短路处距甲地一条输电线的电阻:R′=R=×50Ω=25Ω;
(2)导线总长度:
L==5000m=5km,
短路的地点离甲地的距离:
s=×L=×5km=2.5km.
故答案为:25;2.5.
【点评】本题考查了学生对欧姆定律的掌握和运用,知道短路的地点离甲地的距离为导线总长度的一半是本题的关键.
24.如图所示是一种自动测定油箱内由高度的油量表(是由量程为0~0.6A的电流表改装而成),金属杠杆的右端是滑动变阻器的滑片.从油量表指针所指的刻度,就可以知道油箱内油面的高度.电源电压为12V,定值电阻R0的作用是 保护电路 ;当油箱油面下降时,油量表的示数将 减小 (选填“增大”、“减小”或“不变”);油箱装满油时,油量表为最大值(即电流表达到最大值,此时滑动变阻器的触头在某一端),则R0
的值是 20 Ω.
【分析】(1)如果没有定值电阻的话,则当油箱中的油越来越多的时候,滑动变阻器的阻值就会越来越小,此时电路中的电流就会越来越大,可能会烧坏电流表;
(2)当油箱中的油面下降时,根据滑片的移动可知接入电路中电阻的变化,利用欧姆定律即可得出电流表的示数变化;
(3)当油箱装满汽油时,滑动变阻器接入电路中的电阻为0,电路为R0的简单电路,根据欧姆定律求出R0的阻值.
【解答】解:
(1)由电路图可知,电路中如果没有定值电阻R0,则当滑动变阻器滑片P滑到下端时,电路会短路,会损坏油量表与电源,由此可见,定值电阻R0的作用是:保护电路,避免短路;
(2)由图知,当油箱中的油面下降时,浮标下降,杠杆的右端上升,滑动变阻器接入电路的阻值会变大,电源电压不变,由I=可知,油量表(电流表)的示数会减小;
(2)当油箱装满汽油时,滑动变阻器接入电路中的电阻为0,电路为R0的简单电路,
此时电路中的电流最大为I=0.6A,则R0的阻值:
R0===20Ω.
故答案为:保护电路;减小;20.
【点评】本题考查了定值电阻的作用、电阻的串联和欧姆定律的应用,认真审题,充分理解题意、分析清楚电路结构、熟练应用串联电路特点及欧姆定律即可解题.
25.
如图是甲、乙两导体的电流与电压关系图象,由图可得乙的电阻是 20 Ω,若把甲、乙两电阻串联在电路中,加在甲、乙两电阻上的电压之比U甲:U乙= 1:2 .
【分析】由图象读出电阻甲、乙在电流为1A时所对应的两端电压,然后由欧姆定律求出电阻乙的阻值;根据串联电路特点和欧姆定律计算两电阻串联后电压比.
【解答】解:由图象可知,当通过甲、乙电阻的电流为1A时,甲两端电压为10V,乙两端电压为20V,
由I=可得:
R乙===20Ω,
R甲===10Ω;
若把甲、乙两电阻串联在电路中,根据串联电路中电流处处相等可和欧姆定律可得:
====.
故答案为:20;1:2.
【点评】本题考查串联电路特点和欧姆定律的应用,关键是从图象中能找到有用的信息,确定电阻的大小.
26.如图所示电路,灯泡L1、L2、L3分别标有“6V
3W”、“6V
3.6W”、“10V
5W”字样(不考虑温度对灯丝电阻的影响).
(1)只闭合开关S1时,要使其中一只灯泡正常发光,另一只不烧坏,电源最大电压是 11 V,通电1min灯泡L2产生的热量是 150 J.
(2)如果电源电压为2.4V,要使电流表示数最大,则应闭合开关 S1、S2、S3 ,电流表示数为 0.32 A.
【分析】(1)只闭合开关S1时,灯泡L1、L2串联连接;
已知灯泡的额定电压和额定功率,根据P=UI的变形公式分别求出额定电流,根据串联电流规律可知,能正常发光的只能是额定电流较小的那一个,根据P=求出灯泡L1、L2的阻值,最后根据欧姆定律的应用求出电源电压;
根据Q=I2Rt即可求出通电1min灯泡L2产生的热量;
(2)根据欧姆定律可知,要使电流表示数最大,则电路中的总电阻最小;由串并联电路中电阻的规律可知,当灯泡并联时,电路中的总电阻较小,因此当S1、S2、S3都闭合时,灯泡L1、L3并联,电路总电阻最小;
先根据P=求出灯泡L3的阻值,然后根据并联电路电阻规律求出总电阻,再由欧姆定律求出电路电流,即电流表的示数.
【解答】解:(1)由P=UI可得,IL1===0.5A;
IL2===0.6A;
要使其中一只灯泡正常发光,另一只不烧坏,则电路中的电流为0.5A;
由P=可得:R1===12Ω;
R2===10Ω;
由I=可知,电源电压:U=IR总=0.5A×(12Ω+10Ω)=11V;
通电1min灯泡L2产生的热量:Q=I2R2t=(0.5A)2×10Ω×60s=150J;
(2)根据欧姆定律可知,要使电流表示数最大,则电路中的总电阻最小;由串并联电路中电阻的规律可知,当灯泡并联时,电路中的总电阻较小,因此当S1、S2、S3都闭合时,灯泡L1、L3并联,电路总电阻最小,电流表示数最大;
由P=可得:R3===20Ω;
并联电路中的总电阻:R===7.5Ω;
电流表的示数:I′===0.32A.
故答案为:(1)11;150;(2)S1、S2、S3;0.32A.
【点评】本题是电学的综合计算题目,考查了有关欧姆定律和电功率公式的应用,关键熟练掌握欧姆定律,搞清串并联电路电流、电压以及电阻的特点.
27.如图所示为一种人体秤的工作原理示意图,电源电压恒定不变.体重显示表是由电流表改装而成,定值电阻R0起保护电路作用,其电阻值为10Ω,在人体秤上不施加力时滑片P在电阻R的最上端,施加的力最大时滑片P移至电阻R的最下端,该人体秤测量范围0~100kg,电路中电流变化范围0.1~0.6A,则电源电压为 6 V,滑动变阻器的最大值为 50 Ω.
【分析】由电路图可知,R与R0串联,电流表测电路中的电流.
(1)施加的力最大时滑片P移至电阻R的最下端,电路为R0的简单电路,电流表的示数最大,由题意可知电路中的电流,根据欧姆定律求出电源的电压;
(2)在人体秤上不施加力时滑片P在电阻R的最上端,接入电路中的电阻最大,电路中的电流最小,根据欧姆定律求出电路中的总电阻,利用电阻的串联求出滑动变阻器的最大值.
【解答】解:由电路图可知,R与R0串联,电流表测电路中的电流.
(1)施加的力最大时滑片P移至电阻R的最下端,电路为R0的简单电路,电流表的示数最大,
由I=可得,电源的电压:
U=I大R0=0.6A×10Ω=6V;
(2)在人体秤上不施加力时滑片P在电阻R的最上端,接入电路中的电阻最大,电路中的电流最小,
此时电路中的总电阻:
R总===60Ω,
因串联电路中总电阻等于各分电阻之和,
所以,滑动变阻器的最大值:
R=R总﹣R0=60Ω﹣10Ω=50Ω.
故答案为:6;50.
【点评】本题考查了串联电路的特点和欧姆定律的应用,分清电路中最大和最小电流时电路的连接方式是关键.
28.如图所示,电源电压不变,R1=2Ω,R2=3Ω,R3=4Ω.只闭合S,电流表A1、A2示数之比为 1:1 ,电压表V1、V2示数之比为 1:3 .再闭合S1、S2,电流表A1、A2示数之比为 3:5 ,电压表V1、V2示数之比为 1:1 .
【分析】(1)只闭合S,R1与R3串联,根据串联电路处处电流相等即可得出电流表示数之比,根据U=IR即可求出电压之比.
(2)再闭合S1、S2,R1与R2并联,根据并联电路两端电压相等可知电压表示数之比,根据I=和并联电路的电流特点可求出电流表示数之比.
【解答】解:(1)只闭合S,R1与R3串联,电流表A1、A2测量电路中的电流,由于根据串联电路中处处电流相等,则电流表A1、A2示数之比为1:1;
电压表测量R1两端的电压,电压表V2测量R1与R3两端的总电压,根据I=和串联电路的电阻特点可得:
电压表V1、V2示数之比为U1:U=IR1:I(R1+R3)=R1:(R1+R3)=2Ω:(2Ω+4Ω)=1:3.
(2)再闭合S1、S2,R1与R2并联,电压表V1、V2测量并联电路两端的电压,由于并联电路两端电压相等,所以电压表V1、V2示数之比为1:1;
电流表A1测量R1的电流,电流表A2测量干路电流,根据I=和并联电路的电流特点可得:
电流表示数A1、A2之比为I1′:I′=:(+)=:(+)=:(+)=3:5.
故答案为:1:1;1:3;3:5;1:1.
【点评】本题考查串并联电路的特点和欧姆定律的应用,关键是电路连接方式的判断和电表的测量对象判断.
29.小英按图甲所示的电路图连接实验电路,测量电阻Rx的阻值.闭合开关S,调节滑动变阻器的滑片P后,观察到电压表和电流表的示数分别如图乙、丙所示,则电压表的示数为 2 V,电流表的示数为 0.5 A,待测电阻Rx的阻值为 4 Ω.
【分析】由图根据电表的量程和分度值读出电压表和电流的示数,由I=计算Rx的阻值.
【解答】解:
由图甲知,Rx与R串联,电压表测Rx两端的电压,电流表测电路中电流,
由图乙知,电压表使用0~3V量程,分度值为0.1V,Rx两端电压为2V;
由图丙知,电流表使用0~0.6A量程,分度值0.02A,通过Rx的电流为0.5A;
由I=可得Rx的阻值:
Rx===4Ω.
故答案为:2;0.5;4.
【点评】本题是伏安法测电阻的实验,伏安法测电阻是历年常考查知识点.本题考查的是基本实验技能,要求学生会读电压表、电流表的示数,会利用“伏安法”测电阻.是一道简单题.
30.如图所示,电阻R1标有“6Ω
lA”,R2标有“3Ω
1.2A”,电流表A1、A2的量程均为0~3A,电压表量程0~15V,在a、b间接入电压可调的直流电源.闭合开关s后,为保证R1、R2均不损坏,则允许加的最大电源电压是 3.6V ,通过电流表A1的电流不得超过 1.8A .
【分析】开关闭合后,两电阻并联,电压表测电源的电压,电流表A1测干路电流,电流表A2测通过电阻R2的电流;
(1)根据欧姆定律分别求出两电阻两端允许所加的最大电压,然后根据并联电路的电压特点确定R1、R2均不损坏时允许加的电源电压;
(2)根据欧姆定律求出通过两电阻的电流,再根据并联电路的电流特点求出电流表A1的最大示数.
【解答】解:开关闭合s后,两电阻并联,电压表测电源的电压,电流表A1测干路电流,电流表A2测通过电阻R2的电流,
(1)∵电阻R1标有“6Ω
1A”,R2标有“3Ω
1.2A”,
∴根据欧姆定律可得:
电阻R1两端允许的最大电压为U1=I1R1=1A×6Ω=6V,
电阻R2两端允许的最大电压为U2=I2R2=1.2A×3Ω=3.6V,
∵并联电路,各支路电压相等,且6V>3.6V,
∴为了保护电阻R2,电源电压不能超过3.6V.
(2)此时通过电阻R1的电流为:
I1===0.6A
欧姆定律的应用(2)
(填空部分)
1.在串联电路中,若R1:R2=5:2,则通过两个电阻的电流之比是 ,R1与R2两端的电压之比为 .
2.电阻为12Ω的电铃,正常工作时的电压为6V,现只有一个8V的电源,要使它正常工作,要给它 联一个 Ω的电阻.
3.如图所示,当开关S闭合,甲、乙两表均为电压表时,两表示数之比U甲:U乙=3:1;当开关S断开,甲、乙两表均为电流表时,两表示数之比I甲:I乙= ,相同时间内R1、R2产生的热量之比Q1:Q2= .
4.如图所示的电路,电源电压恒定不变,闭合开关S,将滑动变阻器的滑片P自右向左移动的过程中,电压表示数将 ,电流表示数将 (均选填“变大”、“不变”或“变小”).
5.如图所示,电源电压恒为6V,R1的阻值为8Ω,R2两端的电压为4V,则通过b点的电流为 A,R2的阻值为 Ω.
6.某段金属导体两端电压为4V时,通过的电流是0.2A;当该导体两端电压为12V时,通过该导体的电流为 A;当该导体两端电压降为0时,电阻为 Ω.
7.如图所示,电源电压保持6V不变,电阻R1=10Ω,R2=20Ω,闭合开关S,通电30s,则电阻R1产生的热量为 J.
8.图中电源电压保持不变,灯泡标有“6V
3W”字样,当开关S闭合时,灯泡L正常发光,电流表的实数为0.8A,则电阻R= Ω,通电10s,R产生的热量为 J.
9.如图所示的电路中,电源电压6V保持不变,定值电阻R1为10Ω,滑动变阻器R的最大值为20Ω,当开关S闭合,滑片由右端向最左端滑动的过程中,电流表示数 (选填“变小”、“变大”或“不变”),在此过程中电压表示数的变化范围是 V.
10.如图甲所示的电路中,电源电压保持不变,R0为定值电阻,R为滑动变阻器.闭合开关S后,在移动滑片P的过程中,电流表的示数I与R的阻值关系如图乙所示,电压表的示数U与R的阻值关系如图丙所示,则R0的阻值为 Ω,电源电压为 V.
11.在如图示数的电路中,电源电压保持不变.开关S闭合后,滑片P在滑动变阻器R2的某两点之间滑动的过程中,电流表的示数变化范围是1A﹣2A,电压表的示数变化范围是4V﹣8V.则定值电阻R1= Ω,电源电压U= V.
12.如图是一种自动测定油箱内油面高度的装置,R是滑动变阻器,它的金属滑片连在滑杆的右端,从电流表指针所指的刻度,就可以知道油箱内油面的高度.当油面上升时,电流表的示数 ,定值电阻R0两端的电压 .(均选填“变大”、“变小”或“不变”)
13.
如图所示,开关S闭合后,灯L1、L2都能发光,则甲是 (选填“电压表”或“电流表”),若开关S断开后,灯L1、L2都能发光,且甲、乙两表的示数之比为4:3,则L1、L2电阻之比为 .
14.如图所示的电路中,开关闭合后,滑动变阻器从左向右滑动的过程中,灯泡的亮度 (填“变亮”或“变暗”或“不变”),电压表的示数将 (填“增大”或“减小”).
15.巨磁电阻(GMR)效应是指某些材料的电阻在磁场中急剧减小的现象.如图是巨磁电阻特性原理示意图,GMR是巨磁电阻,电源电压恒定,当开关S1、S2都闭合时,滑动变阻器滑片P向左滑动时,电流表示数将 (“变大”、“变小”或“不变”),指示灯的亮度将 (“变亮”、“变暗”或“不变”).
16.如图是关于电阻R1、R2的电流与电压关系的图象,则R1 R2,若将R1、R2并联接在电压为2V的电路中,则干路的电流为 A.
17.如图所示,电源电压不变,开关S由闭合到断开时,电流表的示数将 ,电压表的示数将 .(选填“增大”、“减小”、“不变”)
18.如图所示的电路中,电源电压恒定,R2=10Ω,开关S、S1都闭合时,电流表示数为0.4A;开关S闭合,开关S1断开时,电流表示数变为0.3A.则电源电压为 V,电阻R1的阻值为 Ω.
19.甲、乙两电阻的电流与电压关系如图所示,由图可知,通过同一电阻的电流与它两端的电压成 (选填“正比”或“反比”),阻值R甲 R乙.(选填“>”、“=”或“<”)
20.如图所示电路中,闭合开关S后,电流表A1的示数为0.5A,电流表A2的示数为0.4A.则通过电阻R2的电流为 A,电阻R1与R2的阻值之比为 .
21.如图所示的电路,电源电压为12V且保持不变.当开关S、S1都闭合,滑动变阻器滑片P置于中点时,电流表示数为1.5A,电阻R= Ω.此时断开S1,电流表示数变为0.6A,则变阻器的最大电阻为 Ω.
22.如图甲所示电路,电源电压不变.闭合开关后,滑片P由b端滑到a端,电压表示数U与电流表示数I的变化关系如图乙所示,则可判断电源电压是 V,定值电阻R的阻值是 Ω,滑动变阻器的最大阻值为 Ω.
23.在相距20km的甲、乙两地之间有两条输电线,已知每1m输电线的电阻为0.01Ω.现输电线在某处发生短路,为确定短路位置,检修员利用电压表、电流表和电源接成如图所示电路进行检测,当电压表的示数为1.5V时,电流表示数为30mA.则短路处距甲地一条输电线的电阻为 Ω,短路位置距甲地的距离为 km.
24.如图所示是一种自动测定油箱内由高度的油量表(是由量程为0~0.6A的电流表改装而成),金属杠杆的右端是滑动变阻器的滑片.从油量表指针所指的刻度,就可以知道油箱内油面的高度.电源电压为12V,定值电阻R0的作用是 ;当油箱油面下降时,油量表的示数将 (选填“增大”、“减小”或“不变”);油箱装满油时,油量表为最大值(即电流表达到最大值,此时滑动变阻器的触头在某一端),则R0
的值是 Ω.
25.
如图是甲、乙两导体的电流与电压关系图象,由图可得乙的电阻是 Ω,若把甲、乙两电阻串联在电路中,加在甲、乙两电阻上的电压之比U甲:U乙= .
26.如图所示电路,灯泡L1、L2、L3分别标有“6V
3W”、“6V
3.6W”、“10V
5W”字样(不考虑温度对灯丝电阻的影响).
(1)只闭合开关S1时,要使其中一只灯泡正常发光,另一只不烧坏,电源最大电压是 V,通电1min灯泡L2产生的热量是 J.
(2)如果电源电压为2.4V,要使电流表示数最大,则应闭合开关 ,电流表示数为 A.
27.如图所示为一种人体秤的工作原理示意图,电源电压恒定不变.体重显示表是由电流表改装而成,定值电阻R0起保护电路作用,其电阻值为10Ω,在人体秤上不施加力时滑片P在电阻R的最上端,施加的力最大时滑片P移至电阻R的最下端,该人体秤测量范围0~100kg,电路中电流变化范围0.1~0.6A,则电源电压为 V,滑动变阻器的最大值为 Ω.
28.如图所示,电源电压不变,R1=2Ω,R2=3Ω,R3=4Ω.只闭合S,电流表A1、A2示数之比为 ,电压表V1、V2示数之比为 .再闭合S1、S2,电流表A1、A2示数之比为 ,电压表V1、V2示数之比为 .
29.小英按图甲所示的电路图连接实验电路,测量电阻Rx的阻值.闭合开关S,调节滑动变阻器的滑片P后,观察到电压表和电流表的示数分别如图乙、丙所示,则电压表的示数为 V,电流表的示数为 A,待测电阻Rx的阻值为 Ω.
30.如图所示,电阻R1标有“6Ω
lA”,R2标有“3Ω
1.2A”,电流表A1、A2的量程均为0~3A,电压表量程0~15V,在a、b间接入电压可调的直流电源.闭合开关s后,为保证R1、R2均不损坏,则允许加的最大电源电压是 ,通过电流表A1的电流不得超过 .
参考答案与解析
1.在串联电路中,若R1:R2=5:2,则通过两个电阻的电流之比是 1:1 ,R1与R2两端的电压之比为 5:2 .
【分析】根据串联电路的电流关系、电压关系求解
【解答】解:∵两个电阻串联
∴I1=I2,即:I1:I2=1:1,
∴U1:U2=R1:R2=5:2
故答案为:1:1,5:2
【点评】灵活运用串联电路的特点(I=I1=I2、U=U1+U2、R=R1+R2)及分压关系
2.电阻为12Ω的电铃,正常工作时的电压为6V,现只有一个8V的电源,要使它正常工作,要给它 串 联一个 4 Ω的电阻.
【分析】比较电铃的电压与电源电压,可知电源电压大于电铃的额定电压,故需要串联一个电阻分压,串联电阻两端的电压等于电源电压减去电铃的额定电压;
因为电铃正常工作,电铃两端的电压等于额定电压,已知电铃的电阻,则利用欧姆定律求此时通过电铃的电流,则串联电阻的阻值利用R=计算.
【解答】解:要使电铃正常工作,需要给电铃串联一个电阻R,串联电阻R两端的电压:
UR=U﹣U额=8V﹣6V=2V,
∵电铃正常工作,
I===0.5A;
则串联电阻R===4Ω;
故答案为:串,4.
【点评】本题考查了学生对欧姆定律、电阻串联特点的掌握和运用,应熟练掌握相关内容并能灵活应用.
3.如图所示,当开关S闭合,甲、乙两表均为电压表时,两表示数之比U甲:U乙=3:1;当开关S断开,甲、乙两表均为电流表时,两表示数之比I甲:I乙= 2:3 ,相同时间内R1、R2产生的热量之比Q1:Q2= 1:2 .
【分析】(1)当开关S闭合,甲、乙两表为电压表时,两电阻串联,甲测电源的电压,乙测R2两端的电压;根据串联电路的电流特点和欧姆定律得出两电阻的阻值之比;
(2)当开关S断开,甲、乙两表为电流表时,两电阻并联,甲测通过R2的电流,乙测干路电流;根据并联电路的电压特点求出通过两支路的电流之比,根据并联电路的电流特点求出两电流表示数的比值;根据并联电路的电压特点和Q=W=求出R1、R2产生的热量之比.
【解答】解:当开关S闭合,甲、乙两表为电压表时,等效电路图如下图所示:
由于串联电路各处的电流相等,根据U=IR可知,
两电压表的示数之比:
====,
解得:
=;
当开关S断开,甲、乙两表为电流表时,等效电路图如下图所示:
由于并联电路各支路两端的电压相等,根据I=可知,
R1和R2的电流之比:
==,
两电流表的示数之比:
===,
由Q=W=t可知,相同时间内R1、R2产生的热量之比:
==.
故答案为:2:3;1:2.
【点评】本题关键有二:一画等效电路图,二理清串联电路的分压关系(U1:U2=R1:R2)和并联电路的电流、电功率的关系(P1:P2=I1:I2=R2:R1)
4.如图所示的电路,电源电压恒定不变,闭合开关S,将滑动变阻器的滑片P自右向左移动的过程中,电压表示数将 变大 ,电流表示数将 不变 (均选填“变大”、“不变”或“变小”).
【分析】由电路图可知,灯泡与滑动变阻器串联,滑动变阻器完全接入电路中,电流表测电路电流,电压表测量滑动变阻器滑片右侧接入电路的电阻两端的电压;
由滑动变阻器滑片方向变化得出滑动变阻器滑片右侧接入电路的电阻阻值变化,从而得出电压表和电流表示数的比值变化.
【解答】解:由电路图可知,灯泡与滑动变阻器串联,滑动变阻器完全接入电路中,电流表测电路中的电流,电压表测量滑动变阻器滑片右侧接入电路的电阻两端的电压;
由于滑动变阻器的电阻全部连入电路,则在滑动变阻器的滑片P自右向左移动的过程中,电路中的总电阻不变,根据欧姆定律可知电路中的电流不变,即电流表示数不变;
由于变阻器滑片右侧接入电路的电阻阻值变大,根据U=IR可知电压表示数变大.
故答案为:变大;不变.
【点评】本题考查了电压表和电流表示数的比值的变化,分析清楚电路结构,明确电压表与电流表所测的量,熟练应用欧姆定律是正确解题的关键.
5.如图所示,电源电压恒为6V,R1的阻值为8Ω,R2两端的电压为4V,则通过b点的电流为 0.25 A,R2的阻值为 16 Ω.
【分析】由电路图可知,R1与R2串联,根据串联电路的电压特点求出电阻R1两端的电压;根据欧姆定律和串联电路的电流特点求出电路中的电流,再根据欧姆定律求出电阻R2的阻值.
【解答】解:由电路图可知,R1与R2串联.
因串联电路中总电压等于各分电压之和,
所以,电阻R1两端的电压:
U1=U﹣U2=6V﹣4V=2V;
因串联电路中各处的电流相等,
所以,通过b点的电流:
Ib=I2=I1===0.25A,
由I=得电阻R2的阻值:
R2===16Ω.
故答案为:0.25;16.
【点评】本题考查了串联电路的特点和欧姆定律的应用,是一道较为简单的应用题.
6.某段金属导体两端电压为4V时,通过的电流是0.2A;当该导体两端电压为12V时,通过该导体的电流为 0.6 A;当该导体两端电压降为0时,电阻为 20 Ω.
【分析】(1)知道导体两端的电压和通过的电流,根据欧姆定律求出导体的电阻;
(2)电阻是导体本身的一种性质,只与导体的材料、长度、横截面积和温度有关,与两端的电压和通过的电流无关,再根据欧姆定律求出当该导体两端电压为12V时通过该导体的电流.
【解答】解:由I=可得,导体的电阻:
R===20Ω,
因电阻是导体本身的一种性质,与两端的电压和通过的电流无关,
所以,当该导体两端电压为12V时或该导体两端电压降为0时,导体的电阻仍为20Ω不变,
当该导体两端电压为12V时,通过该导体的电流:
I′===0.6A.
故答案为:0.6;20.
【点评】本题考查了欧姆定律的简单应用,关键是知道导体的电阻与两端的电压和通过的电流无关,是一道基础题目.
7.如图所示,电源电压保持6V不变,电阻R1=10Ω,R2=20Ω,闭合开关S,通电30s,则电阻R1产生的热量为 12 J.
【分析】根据电阻的串联和欧姆定律求出电路中的电流的电流,再根据Q=I2Rt求出通电30s电阻R1产生的热量.
【解答】解:因串联电路中总电阻等于各分电阻之和,
所以,电路中的电流:
I===0.2A,
则通电30s电阻R1产生的热量:
Q1=I2R1t=(0.2A)2×10Ω×30s=12J.
故答案为:12.
【点评】本题考查了电阻的串联和欧姆定律、焦耳定律的应用,是一道基础题目.
8.图中电源电压保持不变,灯泡标有“6V
3W”字样,当开关S闭合时,灯泡L正常发光,电流表的实数为0.8A,则电阻R= 20 Ω,通电10s,R产生的热量为 18 J.
【分析】因为灯泡和电阻并联,根据P=UI求出灯泡中的电流,再并联电路的电流特点求出电阻中的电流,根据欧姆定律即可求出电阻R的阻值,根据Q=W=UIt求出电阻产生的热量.
【解答】解:当闭合开关S时,灯L正常发光,说明电源电压为U=6V,电流表测的是总电流,则I=0.8A,
由P=UI可知:
灯泡中的电流IL===0.5A,
根据并联电路的干路电流等于各支路电流之和可知:
电阻中的电流IR=I﹣IL=0.8A﹣0.5A=0.3A,
由I=得:
电阻R===20Ω;
通电1min电阻R产生的热量:
Q=W=UIRt=6V×0.3A×10s=18J.
故答案为:20;18.
【点评】本题考查并联电路的特点和欧姆定律、焦耳定律公式的理解和掌握,弄明白电压和电流关系是解决此题的关键.
9.如图所示的电路中,电源电压6V保持不变,定值电阻R1为10Ω,滑动变阻器R的最大值为20Ω,当开关S闭合,滑片由右端向最左端滑动的过程中,电流表示数 变大 (选填“变小”、“变大”或“不变”),在此过程中电压表示数的变化范围是 2V~6 V.
【分析】由电路图可知,定值电阻R1与滑动变阻器R串联,电压表测定值电阻两端的电压,电流表测电路中的电流.
(1)根据滑片的移动可知接入电路中电阻的变化,根据欧姆定律可知电路中电流的变化;
(2)当滑片位于左端时,电路为定值电阻的简单电路,电压表测电源的电压示数最大;当滑片位于右端时,接入电路中的电阻最大,电路中的电流最小,电压表的示数最小,根据电阻的串联和欧姆定律求出电路中的电流,再利于欧姆定律求出电压表的最小示数,然后得出答案.
【解答】解:由电路图可知,定值电阻R1与滑动变阻器R串联,电压表测定值电阻两端的电压,电流表测电路中的电流.
(1)当开关S闭合,滑片由右端向最左端滑动的过程中,接入电路中电阻变小,电路中的总电阻变小,
由I=可知,电路中的电路变大,即电流表的示数变大;
(2)当滑片位于右端时,接入电路中的电阻最大,电路中的电流最小,电压表的示数最小,
因串联电路中总电阻等于各分电压之和,
所以,电路中的最小电流:
I===0.2A,
电压表的最小示数:
U1=IR1=0.2A×10Ω=2V,
当滑片位于左端时,电路为定值电阻的简单电路,电压表测电源的电压,则电压表的最大示数为6V;
所以,在此过程中电压表示数的变化范围为2V~6V.
故答案为:变大;2V~6.
【点评】本题考查了电路的动态分析和串联电路特点以及欧姆定律的应用,要注意滑动变阻器接入电路中的电阻最大时电路中的电流最小.
10.如图甲所示的电路中,电源电压保持不变,R0为定值电阻,R为滑动变阻器.闭合开关S后,在移动滑片P的过程中,电流表的示数I与R的阻值关系如图乙所示,电压表的示数U与R的阻值关系如图丙所示,则R0的阻值为 10 Ω,电源电压为 12 V.
【分析】由电路图可知,R与R0串联,电压表测R0两端的电压,电流表测电路中的电流.由图乙可知,滑动变阻器接入电路中的阻值为20Ω时电路中的电流,根据电阻的串联和欧姆定律表示出电源的电压,根据图丙可知滑动变阻器接入电路中的电阻为30Ω时电压表的示数,根据串联电路的电流特点和欧姆定律表示出电路中的电流,根据电阻的串联和欧姆定律表示出电源的电压,利用电源的电压不变得出方程,解方程求出R0的阻值,进一步求出电源的电压.
【解答】解:由电路图可知,R与R0串联,电压表测R0两端的电压,电流表测电路中的电流.
由图乙可知,滑动变阻器接入电路中的阻值R1=20Ω时,电路中的电流I1=0.4A,
因串联电路中总电阻等于各分电阻之和,
所以,由I=可得,电源的电压:
U=I1(R0+R1)=0.4A×(R0+20Ω),
由图丙可知,滑动变阻器接入电路中的电阻R2=30Ω时,电压表的示数U0=3V,
因串联电路中各处的电流相等,
所以,电路中的电流:
I2==,
电源的电压:
U=I2(R0+R2)=×(R0+30Ω),
因电源的电压不变,
所以,0.4A×(R0+20Ω)=×(R0+30Ω),
整理可得:0.4R02+5Ω×R0﹣90Ω=0,
解得:R0=10Ω,R0=﹣22.5Ω舍去,
电源的电压U=I1(R0+R1)=0.4A×(10Ω+20Ω)=12V.
故答案为:10;12.
【点评】本题考查了串联电路的特点和欧姆定律的应用,从图象中获取滑动变阻器接入电路中的电阻与对应的电流、电压表的示数是关键.
11.在如图示数的电路中,电源电压保持不变.开关S闭合后,滑片P在滑动变阻器R2的某两点之间滑动的过程中,电流表的示数变化范围是1A﹣2A,电压表的示数变化范围是4V﹣8V.则定值电阻R1= 4 Ω,电源电压U= 12 V.
【分析】由电路图可知,电阻R1与滑动变阻器串联,电压表测滑动变阻器两端的电压,电流表测电路中的电流;
当滑片向左移动时接入电路中的电阻变小,电路中的电流变大,滑动变阻器两端的电压变小,据此得出两电表对应的示数关系;根据串联电路的特点和欧姆定律表示出电源的电压,利用电源的电压不变建立等式即可求出R1的阻值和电源的电压.
【解答】解:当电路中的电流为1A时,电压表的示数为8V,
串联电路中各处的电流相等,且总电压等于各分电压之和,
电源的电压:U=I1R1+U滑=1A×R1+8V﹣﹣①
当电路中的电流为2A时,电压表的示数为4V,
电源的电压:
U=I2R1+U滑′=2A×R1+4V﹣﹣②
又因为电源的电压不变,
所以:1A×R1+8V=2A×R1+4V,
解得:R1=4Ω,
电源的电压U=2A×R0+4V=2A×4Ω+4V=12V.
故答案为:4;12.
【点评】本题考查了串联电路的特点和欧姆定律的应用,关键是滑片移动时电压表和电流表示数对应关系的判断.
12.如图是一种自动测定油箱内油面高度的装置,R是滑动变阻器,它的金属滑片连在滑杆的右端,从电流表指针所指的刻度,就可以知道油箱内油面的高度.当油面上升时,电流表的示数 变大 ,定值电阻R0两端的电压 变大 .(均选填“变大”、“变小”或“不变”)
【分析】由电路图可知,R与R0串联,电流表测电路中的电流,根据油面的变化可知浮子位置的变化和指针移到的方向,进一步可知接入电路中电阻的变化,根据欧姆定律可知电路中电流的变化和定值电阻R0两端的电压变化.
【解答】解:由电路图可知,R与R0串联,电流表测电路中的电流,
当油面上升时,浮子上移,指针下移,R的阻值变小,电路中的总电阻变小,
由I=可知,电路中的电流变大,即电流表的示数变大,
由U=IR可知,定值电阻R0两端的电压变大.
故答案为:变大;变大.
【点评】本题考查了电路的动态分析,涉及到滑动变阻器和欧姆定律的应用,分析好油面变化时R阻值的变化是关键.
13.
如图所示,开关S闭合后,灯L1、L2都能发光,则甲是 电压表 (选填“电压表”或“电流表”),若开关S断开后,灯L1、L2都能发光,且甲、乙两表的示数之比为4:3,则L1、L2电阻之比为 3:1 .
【分析】(1)开关S闭合后,灯L1、L2都能发光,根据电压表相当于开路,电流表相当于导线即可判断甲乙表的类型.
(2)当S断开时,两表全是电流表两灯泡才能发光,并且两电灯并联,甲表测总电流,乙表测流过L2的电流,则由欧姆定律可求得两电阻之比;
【解答】解:(1)开关S闭合后,甲乙表必须是相当于开路的电压表,这样电流才能通过灯泡L2、L1,灯L1、L2都能发光.
(2)当S断开时,甲乙表必须是相当于导线的电流表,两灯泡才能发光,并且两电灯并联,甲表测总电流,乙表测流过L2的电流,
已知甲、乙两表的示数之比为4:3,设甲表中电流为I甲=4I,则乙表中电流为I2=I乙=3I,
则由并联电路的电流特点可知,流过R1中的电流I1=I甲﹣I乙=4I﹣3I=I;
由欧姆定律I=可得:
====.
故答案为:电压表;3:1.
【点评】本题考查电压表和电流表的使用特点和串并联电路的特点,在电路中电流表可看成是导线没有电阻,而电压表则看作是断路,则可以明确电路的结构.
14.如图所示的电路中,开关闭合后,滑动变阻器从左向右滑动的过程中,灯泡的亮度 变暗 (填“变亮”或“变暗”或“不变”),电压表的示数将 增大 (填“增大”或“减小”).
【分析】由电路图可知,灯泡与滑动变阻器串联,滑动变阻器从左向右滑动的过程中阻值变大,电路中的电流变小,小灯泡两端的电压变小,其功率变小,故亮度变暗,根据滑动变阻器滑片移动方向判断滑动变阻器接入电路的电阻如何变化,由串联电路的特点判断电压表示数如何变化.
【解答】解:由电路图分析可知,灯泡与滑动变阻器串联;
开关闭合后,滑动变阻器从左向右滑动的过程中,变阻器接入电路的阻值变大,电路中的电阻变大,电流变小,小灯泡两端的电压变小,由P=UI可知灯的电功率变小,故其亮度变暗.
由于电压表测量的是滑动变阻器的电压,滑片P从左向右滑动时,滑动变阻器接入电路的阻值变大,根据串联分压知识可知,滑动变阻器两端的电压变大,即电压表示数变大.
故答案为:变暗;增大.
【点评】本题是一道动态分析题,是常考题型,要掌握这类题的解题思路;分析清楚电路结构、熟练应用串联电路特点及欧姆定律、电功率公式是正确解题的关键.
15.巨磁电阻(GMR)效应是指某些材料的电阻在磁场中急剧减小的现象.如图是巨磁电阻特性原理示意图,GMR是巨磁电阻,电源电压恒定,当开关S1、S2都闭合时,滑动变阻器滑片P向左滑动时,电流表示数将 变大 (“变大”、“变小”或“不变”),指示灯的亮度将 变亮 (“变亮”、“变暗”或“不变”).
【分析】(1)由左图可知,滑动变阻器的滑片P向左滑动过程中接入电路中电阻的变化,根据欧姆定律可知电路中电流的变化,进一步根据影响电磁铁磁场的因素可知其磁场变化,据此可知右图巨磁电阻的变化;
(2)由右图可知,巨磁电阻和灯泡串联,先判断巨磁电阻的变化,根据欧姆定律可知电路中电流的变化,根据P=I2R可知灯泡实际功率的变化,进一步判断亮暗的变化.
【解答】解:
由左图可知,滑动变阻器的滑片P向左滑动过程中接入电路中电阻变小,总电阻减小
电源电压恒定,由I=可知,电路中的电流变大,即电流表示数变大;
因电磁铁磁性的强弱与线圈匝数和通过的电流有关,且匝数不变,通过的电流越大,磁性越强,所以,此时电磁铁的磁性变强;
由右图可知,巨磁电阻和灯泡串联,
因为巨磁电阻在磁场中急剧减小,所以此时巨磁电阻的阻值会变小,电路中的总电阻变小,
由I=可知,可知电路中的电流变大,通过灯泡的电流变大,
因为P=I2R且灯泡的亮暗取决于实际功率的大小,所以,灯泡的实际功率变大,灯泡变亮.
故答案为:变大;变亮.
【点评】本题考查了电路的动态分析,涉及到电磁铁磁性与电流的关系和电功率公式的应用等,判断出巨磁电阻的变化是解题的关键.
16.如图是关于电阻R1、R2的电流与电压关系的图象,则R1 < R2,若将R1、R2并联接在电压为2V的电路中,则干路的电流为 0.5 A.
【分析】将R1、R2并联接在电压为2V的电路中,它们两端的电压相等,根据图象读出通过两电阻的电流,根据欧姆定律比较两电阻的阻值关系,根据并联电路的电流特点求出干路的电流.
【解答】解:将R1、R2并联接在电压为2V的电路中,
因并联电路中各支路两端的电压相等,
所以,两电阻两端的电压均为2V,
由图象可知,通过两电阻的电流分别为I1=0.4A,I2=0.1A,
由I=的变形式R=可知,R1<R2,
因并联电路中干路电流等于各支路电流之和,
所以,干路的电流:
I=I1+I2=0.4A+0.1A=0.5A.
故答案为:<;0.5.
【点评】本题考查了并联电路的特点和欧姆定律的应用,从图象中获取有用的信息是关键.
17.如图所示,电源电压不变,开关S由闭合到断开时,电流表的示数将 减小 ,电压表的示数将 不变 .(选填“增大”、“减小”、“不变”)
【分析】由图知,S闭合时R与L并联,电流表测干路电流,电压表测电源电压;S断开时,只有L连入电路中.由此根据并联电路特点分析判断电表示数变化情况.
【解答】解:
由图知,电压表测电源电压,且电源电压不变,所以开关S由闭合到断开时,电压表的示数将不变;
S闭合时,R与L并联,电流表测干路电流,干路电流等于R与L的电流之和;
S断开时,只有L连入电路中,电流表测L支路的电流;
因为并联电路各支路互不影响,所以S断开后通过L的电流不变,
由于L支路的电流小于干路电流,所以电流表示数减小.
故答案为:减小;不变.
【点评】本题考查了并联电路电流和电压特点的认识和理解,关键是正确分析开关在不同状态下电路的结构.
18.如图所示的电路中,电源电压恒定,R2=10Ω,开关S、S1都闭合时,电流表示数为0.4A;开关S闭合,开关S1断开时,电流表示数变为0.3A.则电源电压为 3 V,电阻R1的阻值为 30 Ω.
【分析】由电路图可知,开关S、S1都闭合时,R1与R2并联,电流表测干路电流;开关S闭合,开关S1断开时,电路为R2的简单电路,电流表测通过R2的电流,根据并联电路中各支路独立工作、互不影响可知通过R2的电流不变,即此时电流表的示数为通过R2的电流,根据欧姆定律求出电源的电压,根据并联电路的电流特点求出通过R1的电流,利用并联电路的电压特点和欧姆定律求出电阻R1的阻值.
【解答】解:由电路图可知,开关S、S1都闭合时,R1与R2并联,电流表测干路电流;
开关S闭合,开关S1断开时,电路为R2的简单电路,电流表测通过R2的电流,
因并联电路中各支路独立工作、互不影响,
所以,通过R2的电流不变,即通过R2的电流I2=0.3A,
由I=可得,电源的电压:
U=I2R2=0.3A×10Ω=3V,
因并联电路中干路电流等于各支路电流之和,
所以,通过R1的电流:
I1=I﹣I2=0.4A﹣0.3A=0.1A,
因并联电路中各支路两端的电压相等,
所以,电阻R1的阻值:
R1===30Ω.
故答案为:3;30.
【点评】本题考查了并联电路的特点和欧姆定律的应用,要注意“并联电路中各支路独立工作、互不影响”特点的应用.
19.甲、乙两电阻的电流与电压关系如图所示,由图可知,通过同一电阻的电流与它两端的电压成 正比 (选填“正比”或“反比”),阻值R甲 < R乙.(选填“>”、“=”或“<”)
【分析】通过读电流与电压关系图象,可判断二者的关系,根据欧姆定律可判断两者阻值的大小关系.
【解答】解:由图可知,电流与电压的变化图象中,都是过原点的斜向上的直线,所以说明通过同一电阻的电流与它两端的电压成正比;
从图象中数据可以看出,当电压一定时,通过甲电阻的电流大,由欧姆定律R=可得,
甲的阻值小于乙的阻值,即R甲<R乙.
故答案为:正比;<.
【点评】本题解答的关键是要学会读取图象,能从中找出正确的信息,并能熟练运用欧姆定律进行分析和判断.
20.如图所示电路中,闭合开关S后,电流表A1的示数为0.5A,电流表A2的示数为0.4A.则通过电阻R2的电流为 0.1 A,电阻R1与R2的阻值之比为 1:4 .
【分析】由电路图可知,电阻R1与R2并联,电流表A1测干路电流,电流表A2测R1电支路的电流,根据并联电路的电流特点求出通过电阻R2的电流,根据并联电路的电压特点和欧姆定律求出电阻R1与R2的阻值之比.
【解答】解:由电路图可知,电阻R1与R2并联,电流表A1测干路电流,电流表A2测R1电支路的电流,
因并联电路中干路电流等于各支路电流之和,
所以,通过电阻R2的电流:
I2=I﹣I1=0.5A﹣0.4A=0.1A,
因并联电路中各支路两端的电压相等,
所以,由I=可得,电阻R1与R2的阻值之比:
====.
故答案为:0.1;1:4.
【点评】本题考查了并联电路的特点和欧姆定律的应用,计算过程要注意各量之间的关系,不要颠倒.
21.如图所示的电路,电源电压为12V且保持不变.当开关S、S1都闭合,滑动变阻器滑片P置于中点时,电流表示数为1.5A,电阻R= 8 Ω.此时断开S1,电流表示数变为0.6A,则变阻器的最大电阻为 24 Ω.
【分析】当开关S、S1都闭合时,滑动变阻器被短路,电路为R的基本电路,电流表测量电路电流,根据欧姆定律的应用即可求出电阻R的阻值;当断开S1后,滑动变阻器与定值电阻串联,电流表测量电路电流,根据欧姆定律的应用求出电路总电阻,根据串联电路电阻规律求出滑动变阻器接入电路的阻值,再根据滑片位于中点可知滑动变阻器的最大阻值.
【解答】解:当开关S、S1都闭合时,滑动变阻器被短路,电路为R的基本电路,电流表测量电路电流;
由I=可知,电阻R===8Ω;
当断开S1后,滑动变阻器与定值电阻串联,电流表测量电路电流;
由I=可知,电路的总电阻:R总===20Ω;
因为串联电路的总电阻等于各部分电阻之和,
所以滑动变阻器接入电路的阻值:R滑=R总﹣R=20Ω﹣8Ω=12Ω;
由于此时滑片在变阻器的中点处,
所以滑动变阻器的最大电阻:R滑大=2R滑=2×12Ω=24Ω.
故答案为:8;24.
【点评】本题考查串联电路的特点以及欧姆定律的应用,关键明确在开关处于不同状态时电路的连接方式.
22.如图甲所示电路,电源电压不变.闭合开关后,滑片P由b端滑到a端,电压表示数U与电流表示数I的变化关系如图乙所示,则可判断电源电压是 9 V,定值电阻R的阻值是 6 Ω,滑动变阻器的最大阻值为 12 Ω.
【分析】由电路图可知,R与滑动变阻器串联,电压表测R两端的电压,电流表测电路中的电流.
(1)当滑片在a端时,电路为R的简单电路,此时电路中的电流最大,电压表的示数就是电源电压,由图乙读出对应的电流和电压,根据欧姆定律求出定值电阻R阻值;
(2)当滑片位于b端时,R与滑动变阻器的最大阻值串联,此时电路中的电流最小,电压表的示数最小,根据图象读出电表示数,根据串联电路的电压特点求出变阻器两端的电压,利用欧姆定律求出滑动变阻器的最大阻值.
【解答】解:(1)当滑片在a端时,电路为R的简单电路,电压表的示数最大,电流表的示数最小,
由图象可知,电源的电压U=9V,电路中的电流I=1.5A,
由I=可知,电阻R的阻值:
R===6Ω;
(2)当滑片位于b端时,R与滑动变阻器的最大阻值串联,此时电路中的电流最小,电压表的示数最大,
由图象可知,R两端的电压UR=3V,电路中的最小电流I′=0.5A,
因串联电路中总电压等于各分电压之和,
所以,滑动变阻器两端的电压:
U滑=U﹣UR=9V﹣3V=6V,
滑动变阻器的最大阻值:
R滑===12Ω.
故答案为:9;6;12.
【点评】本题结合图象考查了串联电路的特点和欧姆定律的应用,关键是明白滑片移动过程中电路的变化情况,应用图象解决问题,这是以后学习的重点.
23.在相距20km的甲、乙两地之间有两条输电线,已知每1m输电线的电阻为0.01Ω.现输电线在某处发生短路,为确定短路位置,检修员利用电压表、电流表和电源接成如图所示电路进行检测,当电压表的示数为1.5V时,电流表示数为30mA.则短路处距甲地一条输电线的电阻为 25 Ω,短路位置距甲地的距离为 2.5 km.
【分析】(1)知道电压表和电流表的示数,利用欧姆定律求出连接短路位置到甲地的两段输电线的电阻值;
(2)已知1m导线的电阻值,然后让总电阻除以一米导线的电阻即可求出导线的长度,从而确定出短路的地点离甲地的距离.
【解答】解:(1)由I=可知,连接短路位置到甲地的两段输电线的电阻值:R===50Ω;
短路处距甲地一条输电线的电阻:R′=R=×50Ω=25Ω;
(2)导线总长度:
L==5000m=5km,
短路的地点离甲地的距离:
s=×L=×5km=2.5km.
故答案为:25;2.5.
【点评】本题考查了学生对欧姆定律的掌握和运用,知道短路的地点离甲地的距离为导线总长度的一半是本题的关键.
24.如图所示是一种自动测定油箱内由高度的油量表(是由量程为0~0.6A的电流表改装而成),金属杠杆的右端是滑动变阻器的滑片.从油量表指针所指的刻度,就可以知道油箱内油面的高度.电源电压为12V,定值电阻R0的作用是 保护电路 ;当油箱油面下降时,油量表的示数将 减小 (选填“增大”、“减小”或“不变”);油箱装满油时,油量表为最大值(即电流表达到最大值,此时滑动变阻器的触头在某一端),则R0
的值是 20 Ω.
【分析】(1)如果没有定值电阻的话,则当油箱中的油越来越多的时候,滑动变阻器的阻值就会越来越小,此时电路中的电流就会越来越大,可能会烧坏电流表;
(2)当油箱中的油面下降时,根据滑片的移动可知接入电路中电阻的变化,利用欧姆定律即可得出电流表的示数变化;
(3)当油箱装满汽油时,滑动变阻器接入电路中的电阻为0,电路为R0的简单电路,根据欧姆定律求出R0的阻值.
【解答】解:
(1)由电路图可知,电路中如果没有定值电阻R0,则当滑动变阻器滑片P滑到下端时,电路会短路,会损坏油量表与电源,由此可见,定值电阻R0的作用是:保护电路,避免短路;
(2)由图知,当油箱中的油面下降时,浮标下降,杠杆的右端上升,滑动变阻器接入电路的阻值会变大,电源电压不变,由I=可知,油量表(电流表)的示数会减小;
(2)当油箱装满汽油时,滑动变阻器接入电路中的电阻为0,电路为R0的简单电路,
此时电路中的电流最大为I=0.6A,则R0的阻值:
R0===20Ω.
故答案为:保护电路;减小;20.
【点评】本题考查了定值电阻的作用、电阻的串联和欧姆定律的应用,认真审题,充分理解题意、分析清楚电路结构、熟练应用串联电路特点及欧姆定律即可解题.
25.
如图是甲、乙两导体的电流与电压关系图象,由图可得乙的电阻是 20 Ω,若把甲、乙两电阻串联在电路中,加在甲、乙两电阻上的电压之比U甲:U乙= 1:2 .
【分析】由图象读出电阻甲、乙在电流为1A时所对应的两端电压,然后由欧姆定律求出电阻乙的阻值;根据串联电路特点和欧姆定律计算两电阻串联后电压比.
【解答】解:由图象可知,当通过甲、乙电阻的电流为1A时,甲两端电压为10V,乙两端电压为20V,
由I=可得:
R乙===20Ω,
R甲===10Ω;
若把甲、乙两电阻串联在电路中,根据串联电路中电流处处相等可和欧姆定律可得:
====.
故答案为:20;1:2.
【点评】本题考查串联电路特点和欧姆定律的应用,关键是从图象中能找到有用的信息,确定电阻的大小.
26.如图所示电路,灯泡L1、L2、L3分别标有“6V
3W”、“6V
3.6W”、“10V
5W”字样(不考虑温度对灯丝电阻的影响).
(1)只闭合开关S1时,要使其中一只灯泡正常发光,另一只不烧坏,电源最大电压是 11 V,通电1min灯泡L2产生的热量是 150 J.
(2)如果电源电压为2.4V,要使电流表示数最大,则应闭合开关 S1、S2、S3 ,电流表示数为 0.32 A.
【分析】(1)只闭合开关S1时,灯泡L1、L2串联连接;
已知灯泡的额定电压和额定功率,根据P=UI的变形公式分别求出额定电流,根据串联电流规律可知,能正常发光的只能是额定电流较小的那一个,根据P=求出灯泡L1、L2的阻值,最后根据欧姆定律的应用求出电源电压;
根据Q=I2Rt即可求出通电1min灯泡L2产生的热量;
(2)根据欧姆定律可知,要使电流表示数最大,则电路中的总电阻最小;由串并联电路中电阻的规律可知,当灯泡并联时,电路中的总电阻较小,因此当S1、S2、S3都闭合时,灯泡L1、L3并联,电路总电阻最小;
先根据P=求出灯泡L3的阻值,然后根据并联电路电阻规律求出总电阻,再由欧姆定律求出电路电流,即电流表的示数.
【解答】解:(1)由P=UI可得,IL1===0.5A;
IL2===0.6A;
要使其中一只灯泡正常发光,另一只不烧坏,则电路中的电流为0.5A;
由P=可得:R1===12Ω;
R2===10Ω;
由I=可知,电源电压:U=IR总=0.5A×(12Ω+10Ω)=11V;
通电1min灯泡L2产生的热量:Q=I2R2t=(0.5A)2×10Ω×60s=150J;
(2)根据欧姆定律可知,要使电流表示数最大,则电路中的总电阻最小;由串并联电路中电阻的规律可知,当灯泡并联时,电路中的总电阻较小,因此当S1、S2、S3都闭合时,灯泡L1、L3并联,电路总电阻最小,电流表示数最大;
由P=可得:R3===20Ω;
并联电路中的总电阻:R===7.5Ω;
电流表的示数:I′===0.32A.
故答案为:(1)11;150;(2)S1、S2、S3;0.32A.
【点评】本题是电学的综合计算题目,考查了有关欧姆定律和电功率公式的应用,关键熟练掌握欧姆定律,搞清串并联电路电流、电压以及电阻的特点.
27.如图所示为一种人体秤的工作原理示意图,电源电压恒定不变.体重显示表是由电流表改装而成,定值电阻R0起保护电路作用,其电阻值为10Ω,在人体秤上不施加力时滑片P在电阻R的最上端,施加的力最大时滑片P移至电阻R的最下端,该人体秤测量范围0~100kg,电路中电流变化范围0.1~0.6A,则电源电压为 6 V,滑动变阻器的最大值为 50 Ω.
【分析】由电路图可知,R与R0串联,电流表测电路中的电流.
(1)施加的力最大时滑片P移至电阻R的最下端,电路为R0的简单电路,电流表的示数最大,由题意可知电路中的电流,根据欧姆定律求出电源的电压;
(2)在人体秤上不施加力时滑片P在电阻R的最上端,接入电路中的电阻最大,电路中的电流最小,根据欧姆定律求出电路中的总电阻,利用电阻的串联求出滑动变阻器的最大值.
【解答】解:由电路图可知,R与R0串联,电流表测电路中的电流.
(1)施加的力最大时滑片P移至电阻R的最下端,电路为R0的简单电路,电流表的示数最大,
由I=可得,电源的电压:
U=I大R0=0.6A×10Ω=6V;
(2)在人体秤上不施加力时滑片P在电阻R的最上端,接入电路中的电阻最大,电路中的电流最小,
此时电路中的总电阻:
R总===60Ω,
因串联电路中总电阻等于各分电阻之和,
所以,滑动变阻器的最大值:
R=R总﹣R0=60Ω﹣10Ω=50Ω.
故答案为:6;50.
【点评】本题考查了串联电路的特点和欧姆定律的应用,分清电路中最大和最小电流时电路的连接方式是关键.
28.如图所示,电源电压不变,R1=2Ω,R2=3Ω,R3=4Ω.只闭合S,电流表A1、A2示数之比为 1:1 ,电压表V1、V2示数之比为 1:3 .再闭合S1、S2,电流表A1、A2示数之比为 3:5 ,电压表V1、V2示数之比为 1:1 .
【分析】(1)只闭合S,R1与R3串联,根据串联电路处处电流相等即可得出电流表示数之比,根据U=IR即可求出电压之比.
(2)再闭合S1、S2,R1与R2并联,根据并联电路两端电压相等可知电压表示数之比,根据I=和并联电路的电流特点可求出电流表示数之比.
【解答】解:(1)只闭合S,R1与R3串联,电流表A1、A2测量电路中的电流,由于根据串联电路中处处电流相等,则电流表A1、A2示数之比为1:1;
电压表测量R1两端的电压,电压表V2测量R1与R3两端的总电压,根据I=和串联电路的电阻特点可得:
电压表V1、V2示数之比为U1:U=IR1:I(R1+R3)=R1:(R1+R3)=2Ω:(2Ω+4Ω)=1:3.
(2)再闭合S1、S2,R1与R2并联,电压表V1、V2测量并联电路两端的电压,由于并联电路两端电压相等,所以电压表V1、V2示数之比为1:1;
电流表A1测量R1的电流,电流表A2测量干路电流,根据I=和并联电路的电流特点可得:
电流表示数A1、A2之比为I1′:I′=:(+)=:(+)=:(+)=3:5.
故答案为:1:1;1:3;3:5;1:1.
【点评】本题考查串并联电路的特点和欧姆定律的应用,关键是电路连接方式的判断和电表的测量对象判断.
29.小英按图甲所示的电路图连接实验电路,测量电阻Rx的阻值.闭合开关S,调节滑动变阻器的滑片P后,观察到电压表和电流表的示数分别如图乙、丙所示,则电压表的示数为 2 V,电流表的示数为 0.5 A,待测电阻Rx的阻值为 4 Ω.
【分析】由图根据电表的量程和分度值读出电压表和电流的示数,由I=计算Rx的阻值.
【解答】解:
由图甲知,Rx与R串联,电压表测Rx两端的电压,电流表测电路中电流,
由图乙知,电压表使用0~3V量程,分度值为0.1V,Rx两端电压为2V;
由图丙知,电流表使用0~0.6A量程,分度值0.02A,通过Rx的电流为0.5A;
由I=可得Rx的阻值:
Rx===4Ω.
故答案为:2;0.5;4.
【点评】本题是伏安法测电阻的实验,伏安法测电阻是历年常考查知识点.本题考查的是基本实验技能,要求学生会读电压表、电流表的示数,会利用“伏安法”测电阻.是一道简单题.
30.如图所示,电阻R1标有“6Ω
lA”,R2标有“3Ω
1.2A”,电流表A1、A2的量程均为0~3A,电压表量程0~15V,在a、b间接入电压可调的直流电源.闭合开关s后,为保证R1、R2均不损坏,则允许加的最大电源电压是 3.6V ,通过电流表A1的电流不得超过 1.8A .
【分析】开关闭合后,两电阻并联,电压表测电源的电压,电流表A1测干路电流,电流表A2测通过电阻R2的电流;
(1)根据欧姆定律分别求出两电阻两端允许所加的最大电压,然后根据并联电路的电压特点确定R1、R2均不损坏时允许加的电源电压;
(2)根据欧姆定律求出通过两电阻的电流,再根据并联电路的电流特点求出电流表A1的最大示数.
【解答】解:开关闭合s后,两电阻并联,电压表测电源的电压,电流表A1测干路电流,电流表A2测通过电阻R2的电流,
(1)∵电阻R1标有“6Ω
1A”,R2标有“3Ω
1.2A”,
∴根据欧姆定律可得:
电阻R1两端允许的最大电压为U1=I1R1=1A×6Ω=6V,
电阻R2两端允许的最大电压为U2=I2R2=1.2A×3Ω=3.6V,
∵并联电路,各支路电压相等,且6V>3.6V,
∴为了保护电阻R2,电源电压不能超过3.6V.
(2)此时通过电阻R1的电流为:
I1===0.6A
同课章节目录
- 第十一章 简单机械和功
- 1 杠杆
- 2 滑轮
- 3 功
- 4 功率
- 5 机械效率
- 第十二章 机械能和内能
- 1 动能 势能 机械能
- 2 内能 热传递
- 3 物质的比热容
- 4 机械能和内能的相互转化
- 第十三章 电路初探
- 1 初识家用电器和电路
- 2 电路连接的基本方式
- 3 电流和电流表的使用
- 4 电压和电压表的使用
- 第十四章 欧姆定律
- 1 电阻
- 2 变阻器
- 3 欧姆定律
- 4 欧姆定律的应用
- 第十五章 电功和电热
- 电能表与电功
- 电功率
- 电热器 电流的热效应
- 家庭电路与安全用电
- 第十六章 电磁转换
- 磁体与磁场
- 电流的磁场
- 磁场对电流的作用 电动机
- 安装直流电动机模型
- 电磁感应 发电机
- 第十七章 电磁波与现代通信
- 信息与信息传播
- 电磁波及其传播
- 现代通信 走进信息时代
- 第十八章 能源与可持续发展
- 能源利用与社会发展
- 核能
- 太阳能
- 能量转化的基本规律
- 能源与可持续发展
