平行线判定1
图片预览

文档简介
5.2.2 平行线的判定(一)
一、教学目标:
1、知识与技能
理解“同位角相等,两直线平行”平行线判定公理;会用此公理判定两直线的平行关系。
2、过程与方法
经历直观感知、操作确认、抽象概括和初步的理性思辨的公理发现过程,体验以数表形的数形结合思想。
在公理的运用过程中,发展推理能力和有条理的数学表达能力。
3、情感与态度
感受“数学源于生活,高于生活,用于生活”,感受数学的应用价值。
在数学的探究过程中感受发现的快乐。
二、重难点:
重点:平行线判定公理的理解与应用。
难点:平行线判定公理的发现及公理应用时有条理的表述。
三、教法与学法:
1、采用“创设情境——提出问题——数学探究——发现公理——应用公理”的课堂教学模式和“直观感知——操作确认——抽象概括——初步理性思辨”的公理发现过程。
2、结合具体的平面图形,应用公理和推论进行数学演绎推理,通过开放性问题的解决,培养学生思维的灵活性.结合解题后的反思,总结出应用公理判定平行线中的“找同位角——说明相等——判断平行”程序,提炼以数表形的数形结合和化归思想方法。
四、教学过程:
(一)创设情景,提出问题
1、生活中的平行线(投影出示),寻找身边的平行线。
如:教室中的平行线、楼梯栏杆、笔直的火车铁轨
2、生活中需要平行线,如笔直的火车铁轨;怎样判断两直线平行?你会设计平行线吗?(引出课题)
(二)师生互动,探究新知
1、你会判断如图的两条线段是否平行?
2、请你试试画平行线。
3、师生交流画出的两直线会平行的可能原因…… 得出“同位角相等,两直线平行”
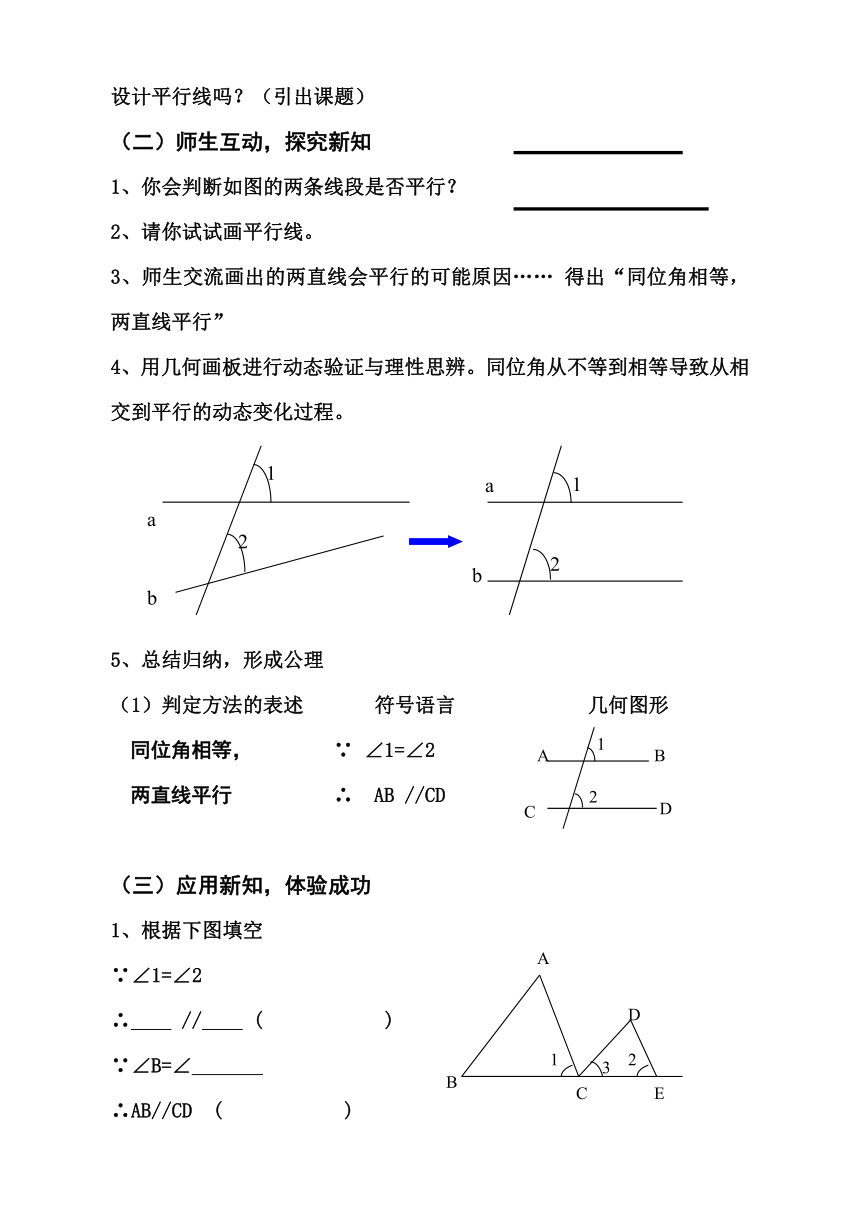
4、用几何画板进行动态验证与理性思辨。同位角从不等到相等导致从相交到平行的动态变化过程。
5、总结归纳,形成公理
(1)判定方法的表述 符号语言 几何图形
同位角相等, ∵ ∠1=∠2
两直线平行 ∴ AB //CD
(三)应用新知,体验成功
1、根据下图填空
∵∠1=∠2
∴ // ( )
∵∠B=∠
∴AB//CD ( )
2、如图,已知直线被直线所截,∠1=45度 ∠2=135度,判断是否平行,并说明理由。
总结: 判定方法运用的基本程序:
变式:上图中,已知直线被直线所截,∠1=52度,请添加一个角度数 ,使,并说明理由。
(四)应用拓展,小结提炼
1、你能说出木工师傅用角尺在长方体上画平行线的道理吗?
2、“在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线互相平行”,这句话是否正确?请说明理由。
总结:又一种判定两直线平行的方法:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线互相平行。
∵a⊥m, b⊥m
∴a∥b
3、思考:没有任何工具,能检验一张纸条的两边沿是否平行吗?
(五)梳理总结,深化提高
回顾本节课的学习,思考下面问题,并把你的想法与同学交流。
1、 你学会了哪些判定两直线平行的方法?
2、 你是怎样得到这些方法的?
3、 在应用这些判定直线平行的方法时往往应分哪几步思考?
4、 你还有哪些体会和疑惑?
(六)作业布置
1、必做题:作业本(2)第5页
2、选做题:探究平行线是否还有其它的判定方法。
1
2
a
b
a
b
1
2
E
2
C
D
B
A
1
3
找同位角
说明相等
判断平行
文字表述
图形特征
符号语言
2
1
A
B
C
D
a
b
m
m
2
1
l
n
4
5
一、教学目标:
1、知识与技能
理解“同位角相等,两直线平行”平行线判定公理;会用此公理判定两直线的平行关系。
2、过程与方法
经历直观感知、操作确认、抽象概括和初步的理性思辨的公理发现过程,体验以数表形的数形结合思想。
在公理的运用过程中,发展推理能力和有条理的数学表达能力。
3、情感与态度
感受“数学源于生活,高于生活,用于生活”,感受数学的应用价值。
在数学的探究过程中感受发现的快乐。
二、重难点:
重点:平行线判定公理的理解与应用。
难点:平行线判定公理的发现及公理应用时有条理的表述。
三、教法与学法:
1、采用“创设情境——提出问题——数学探究——发现公理——应用公理”的课堂教学模式和“直观感知——操作确认——抽象概括——初步理性思辨”的公理发现过程。
2、结合具体的平面图形,应用公理和推论进行数学演绎推理,通过开放性问题的解决,培养学生思维的灵活性.结合解题后的反思,总结出应用公理判定平行线中的“找同位角——说明相等——判断平行”程序,提炼以数表形的数形结合和化归思想方法。
四、教学过程:
(一)创设情景,提出问题
1、生活中的平行线(投影出示),寻找身边的平行线。
如:教室中的平行线、楼梯栏杆、笔直的火车铁轨
2、生活中需要平行线,如笔直的火车铁轨;怎样判断两直线平行?你会设计平行线吗?(引出课题)
(二)师生互动,探究新知
1、你会判断如图的两条线段是否平行?
2、请你试试画平行线。
3、师生交流画出的两直线会平行的可能原因…… 得出“同位角相等,两直线平行”
4、用几何画板进行动态验证与理性思辨。同位角从不等到相等导致从相交到平行的动态变化过程。
5、总结归纳,形成公理
(1)判定方法的表述 符号语言 几何图形
同位角相等, ∵ ∠1=∠2
两直线平行 ∴ AB //CD
(三)应用新知,体验成功
1、根据下图填空
∵∠1=∠2
∴ // ( )
∵∠B=∠
∴AB//CD ( )
2、如图,已知直线被直线所截,∠1=45度 ∠2=135度,判断是否平行,并说明理由。
总结: 判定方法运用的基本程序:
变式:上图中,已知直线被直线所截,∠1=52度,请添加一个角度数 ,使,并说明理由。
(四)应用拓展,小结提炼
1、你能说出木工师傅用角尺在长方体上画平行线的道理吗?
2、“在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线互相平行”,这句话是否正确?请说明理由。
总结:又一种判定两直线平行的方法:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线互相平行。
∵a⊥m, b⊥m
∴a∥b
3、思考:没有任何工具,能检验一张纸条的两边沿是否平行吗?
(五)梳理总结,深化提高
回顾本节课的学习,思考下面问题,并把你的想法与同学交流。
1、 你学会了哪些判定两直线平行的方法?
2、 你是怎样得到这些方法的?
3、 在应用这些判定直线平行的方法时往往应分哪几步思考?
4、 你还有哪些体会和疑惑?
(六)作业布置
1、必做题:作业本(2)第5页
2、选做题:探究平行线是否还有其它的判定方法。
1
2
a
b
a
b
1
2
E
2
C
D
B
A
1
3
找同位角
说明相等
判断平行
文字表述
图形特征
符号语言
2
1
A
B
C
D
a
b
m
m
2
1
l
n
4
5
