1.3一元二次方程的应用（2

课件16张PPT。1.3 一元二次方程的应用（3）湖南省新邵县酿溪中学王军旗学习目标 会熟练的列出一元二次方程解应用题，并能根据具体问题的实际意义，检查其结果是否合理。
重点：熟练的列出一元二次方程解决实际问题。
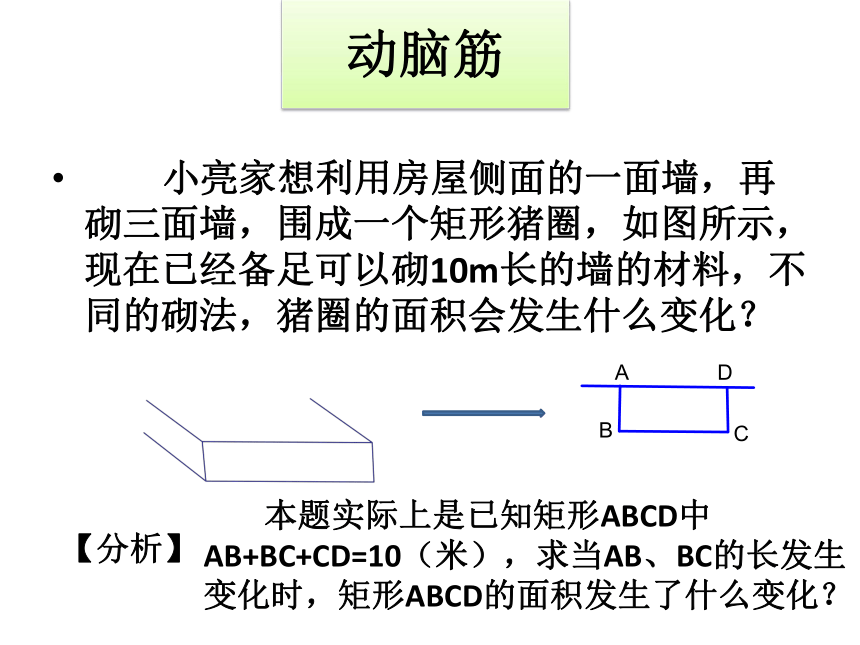
难点：将实际问题抽象为为一元二次方程模型。动脑筋 小亮家想利用房屋侧面的一面墙，再砌三面墙，围成一个矩形猪圈，如图所示，现在已经备足可以砌10m长的墙的材料，不同的砌法，猪圈的面积会发生什么变化？【分析】 本题实际上是已知矩形ABCD中AB+BC+CD=10（米），求当AB、BC的长发生变化时，矩形ABCD的面积发生了什么变化？探究1如果每条边砌一样长，那么每条边的长度
为____（ cm）按这样的砌法，猪圈的面积是_____
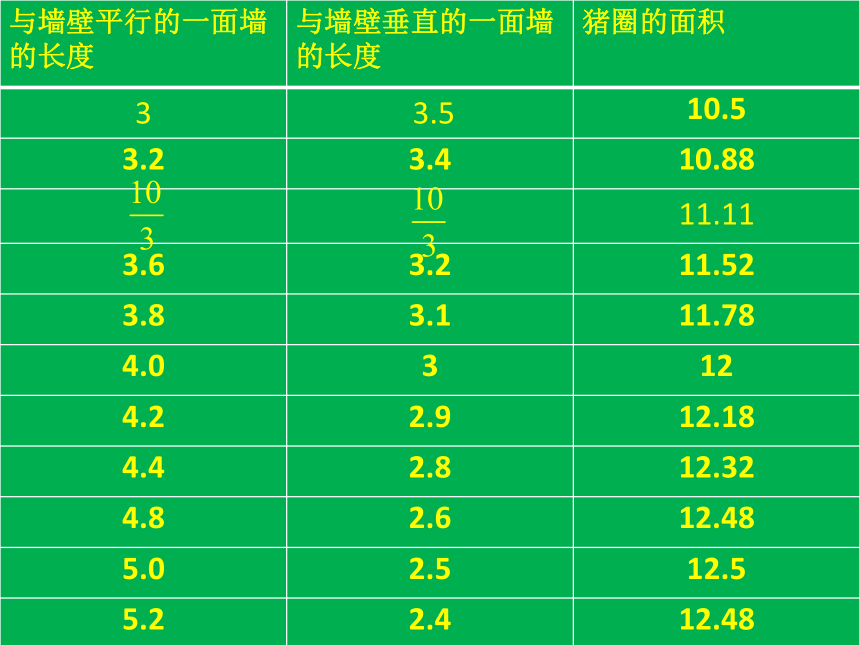
探究2 直观的想，若充分利用墙壁，与墙壁平行的一边应该长一些，那么当与墙壁平行的一面墙比平均长度小些或大些，矩形的面积会发生什么变化呢？求填写P26的表，并寻找规律。
观察上表：1.当与墙平行的一面从 减少时，猪圈的面积发生了什么变化？_______减少3.在上面的表格中与墙壁平行的一面等于多少时，猪圈的面积最大？与墙壁平行的一面等于5m时，猪圈的面积最大为12.5m2
4.有没有一种砌法使猪圈的面积大于12.5 m2？解：假设有一种砌法能是猪圈的面积等于12.55m2，设与墙壁垂直的一面的长为xm,那么与墙壁平行的一面长度为（10-2x）m，
依题意，得：x(10-2x)=12.55, 方程化为：这个方程没有实数解，所以，猪圈的面积不可能大于12.55 m2 5.为什么没有一种砌法使猪圈的面积大于12.5 m2呢？ 设猪圈的面积为y m2，与墙壁垂直的一面的长度为xm,
所以，没有一种砌法使猪圈的面积大于12.5 m2呢？1 .经过调查研究，某工厂生产一种产品的总利润L(元)与产品x（件）的关系为：L=-x2+2000x-10000（0解：(1)依题意，得：-x2+2000x-10000=990000化为：x2-2000x=-1000000，配方，得：x2-2000x+10002=-1000000+10002（x-1000）2=0, x1=x2=1000(2)假设总利润可以达到99.1万元则：依题意，得：-x2+2000x-10000=991000化为：x2-2000x=-1001000，配方，得：x2-2000x+10002=-1001000+10002（x-1000）2=-1000<0.此方程无解。所以，总利润可不可以达到99.1万元2.经过调查研究，某工厂生产一种产品的总利润P(元/件)与产品x件的关系为：
L= -4p2+1360p-93200, ﹙100≤P＜145﹚,
(1)当销售价格P定为多少时，可以使总利润达到22400元？
（2）总利润可以不可以达到22500元？
解：（1）依题意，得：-4p2+1360p-93200=22400,化为：p2-340p=-28900,配方，得：p2-340p+1702=-28900+1702（p-170）2=0, p1=p2=170当销售价格P定为170元时，可以使总利润达到22400元。（2）假设总利润可以达到22500元。依题意，得：-4p2+1360p-93200=22500,化为：p2-340p=-28925,配方，得：p2-340p+1702=-28925+1702（p-170）2=-25<0,所以，此方程无解。因此，总利润不可以达到22500元小结： 解一元二次方程应用题，要善于把实际问题转化为方程问题。因此要注意寻找等量关系。求出方程的解后，要注意检查方程的解是否合理。作业P 28 B 3 2 某商场从厂家以每件40元的价格购进一批商品，当商场按单价50元出售时，能卖500个，已知该商场每涨价1元，其销售量就会减少10个，为了赚8000元利润，售价应定为多少？这时进供货多少个？【分析】1.利润=8000，2.利润=每个利润×数量。
设涨价x元，则x(500-10x)=8000
设定价为x元，则（50-x)[500-10(x-40)]