华师大版数学九年级上册课件23.4中位线(三角形中位线) (共20张PPT)
文档属性
| 名称 | 华师大版数学九年级上册课件23.4中位线(三角形中位线) (共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-21 00:00:00 | ||
图片预览






文档简介
课件20张PPT。§23.4 中 位 线回忆相似三角形有哪些性质?1、相似三角形的对应边成比例,对应角相等。
2、相似三角形对应高的比、对应中线的比、对应角平分线的比、周长的比
都等于相似比。
3、相似三角形的面积比等于相似比的平方。相似三角形有哪些判定方法?1、平行于三角形一边的直线,和其他两边(或两边的延长线)相交所构成的三角形与原三角形相似。
2、两角分别相等的两个三角形相似。
3、两边成比例且夹角相等的两个三角形相似。
4、三边成比例的两个三角形相似。
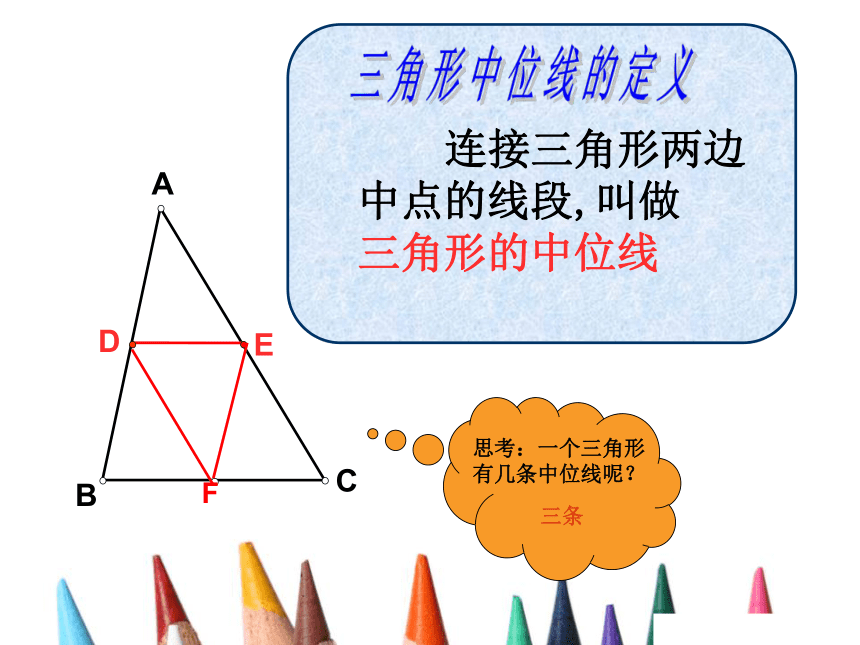
三角形的中位线CBAED 连接三角形两边中点的线段,叫做 三角形的中位线
三角形中位线的定义思考:一个三角形
有几条中位线呢?三条FAF是△ABC的中线DE是△ ABC 的中位线CBAFED三角形中位线要和我们曾经学过的三角形的哪个元素区分开来?中线三角形的中位线有哪些性质呢?
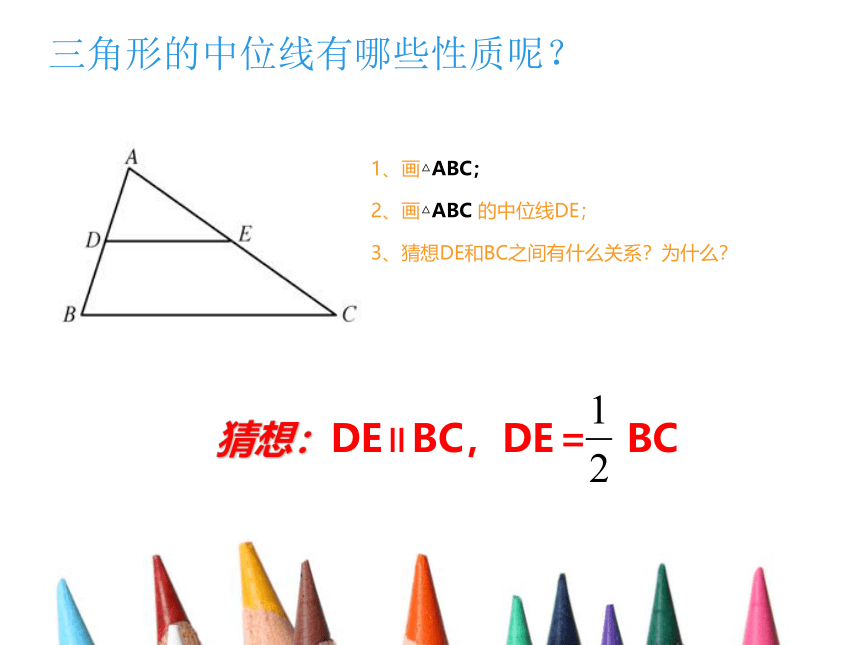
1、画△ABC;
2、画△ABC 的中位线DE;
3、猜想DE和BC之间有什么关系?为什么?
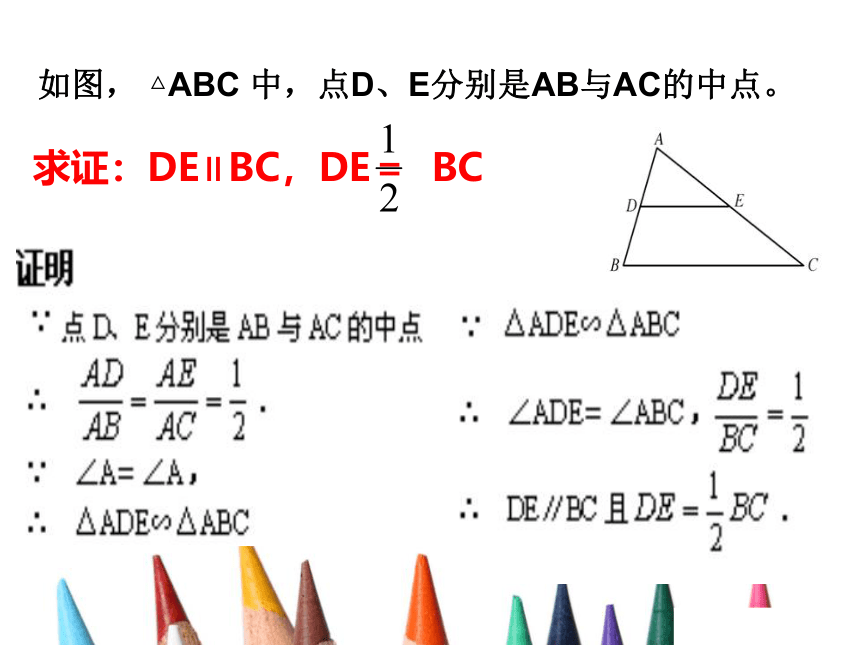
猜想:DE∥BC,DE= BC 如图, △ABC 中,点D、E分别是AB与AC的中点。求证:DE∥BC,DE= BC.三角形中位线的性质三角形中位线平行于第三边,并且等于第三边的一半。三角形中位线定理有两个结论:(1)表示位置关系------平行于第三边;(2)表示数量关系------等于第三边的一半。应用时要具体分析,
需要哪一个就用哪一
个. ∵点D、E分别是AB与AC的中点∴ DE∥BC,DE= BC.中位线性质的常见表达形式: ∵DE是△ABC 的中位线∴ DE∥BC,DE= BC如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么? 如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm图260412BACD EF543实际问题:
A、B两点被岛屿隔开,如何才能知道它们之间的距离呢?AB(1)在A、B外选一点C,连结A C和BC ;(2)并分别找出A C和BC的中点M、N 。(3)连结MN ,并测量MN的长度。解决方案(4)因此MN是△ ABC的中位线,根据三角形中位线定理
AB=2MN。例1 求证:三角形的一条中位线与第三边上的中线互相平分.已知:如图,在△ABC中,AD=DB,BE=EC,AF=FC.
求证:AE、DF互相平分.例1 求证:三角形的一条中位线与第三边上的中线互相平分.已知:如图,在△ABC中,AD=DB,BE=EC,AF=FC.
求证:AE、DF互相平分.证明 连结DE、EF.
∵ AD=DB,BE=EC,
∴ DE∥AC(三角形的中位线平行于第三边并且等于第三边的一半).
同理可得:EF∥AB.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分(平行四边形的对角线互相平分). 例2 如图,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.
求证: 例2 如图,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.
求证: 证明 :连结ED, ∵ D、E分别是边BC、AB的中点,(三角形的中位线平行于第三边并且等于第三边的一半), ∴ △ACG∽△DEG,拓展如果在图24.4.4中,取AC的中点F,假设BF与AD交于G′,如图24.4.5那么我们同理有:
所以有:
即两图中的点G与G′是重合的. 三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线
的长是对应中线长的 。.说一说你学到了什么?1、练习 第1、2题
2、习题23.4 第1、2、3、4题 再见!
2、相似三角形对应高的比、对应中线的比、对应角平分线的比、周长的比
都等于相似比。
3、相似三角形的面积比等于相似比的平方。相似三角形有哪些判定方法?1、平行于三角形一边的直线,和其他两边(或两边的延长线)相交所构成的三角形与原三角形相似。
2、两角分别相等的两个三角形相似。
3、两边成比例且夹角相等的两个三角形相似。
4、三边成比例的两个三角形相似。
三角形的中位线CBAED 连接三角形两边中点的线段,叫做 三角形的中位线
三角形中位线的定义思考:一个三角形
有几条中位线呢?三条FAF是△ABC的中线DE是△ ABC 的中位线CBAFED三角形中位线要和我们曾经学过的三角形的哪个元素区分开来?中线三角形的中位线有哪些性质呢?
1、画△ABC;
2、画△ABC 的中位线DE;
3、猜想DE和BC之间有什么关系?为什么?
猜想:DE∥BC,DE= BC 如图, △ABC 中,点D、E分别是AB与AC的中点。求证:DE∥BC,DE= BC.三角形中位线的性质三角形中位线平行于第三边,并且等于第三边的一半。三角形中位线定理有两个结论:(1)表示位置关系------平行于第三边;(2)表示数量关系------等于第三边的一半。应用时要具体分析,
需要哪一个就用哪一
个. ∵点D、E分别是AB与AC的中点∴ DE∥BC,DE= BC.中位线性质的常见表达形式: ∵DE是△ABC 的中位线∴ DE∥BC,DE= BC如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么? 如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm图260412BACD EF543实际问题:
A、B两点被岛屿隔开,如何才能知道它们之间的距离呢?AB(1)在A、B外选一点C,连结A C和BC ;(2)并分别找出A C和BC的中点M、N 。(3)连结MN ,并测量MN的长度。解决方案(4)因此MN是△ ABC的中位线,根据三角形中位线定理
AB=2MN。例1 求证:三角形的一条中位线与第三边上的中线互相平分.已知:如图,在△ABC中,AD=DB,BE=EC,AF=FC.
求证:AE、DF互相平分.例1 求证:三角形的一条中位线与第三边上的中线互相平分.已知:如图,在△ABC中,AD=DB,BE=EC,AF=FC.
求证:AE、DF互相平分.证明 连结DE、EF.
∵ AD=DB,BE=EC,
∴ DE∥AC(三角形的中位线平行于第三边并且等于第三边的一半).
同理可得:EF∥AB.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分(平行四边形的对角线互相平分). 例2 如图,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.
求证: 例2 如图,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.
求证: 证明 :连结ED, ∵ D、E分别是边BC、AB的中点,(三角形的中位线平行于第三边并且等于第三边的一半), ∴ △ACG∽△DEG,拓展如果在图24.4.4中,取AC的中点F,假设BF与AD交于G′,如图24.4.5那么我们同理有:
所以有:
即两图中的点G与G′是重合的. 三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的连线
的长是对应中线长的 。.说一说你学到了什么?1、练习 第1、2题
2、习题23.4 第1、2、3、4题 再见!
