全等三角形的灵活运用

第五章 全等三角形 灵活运用
全等三角形的判别方法：SSS、ASA、AAS、SAS
全等三角形的性质：全等三角形的对应边相等
全等三角形的对应角相等
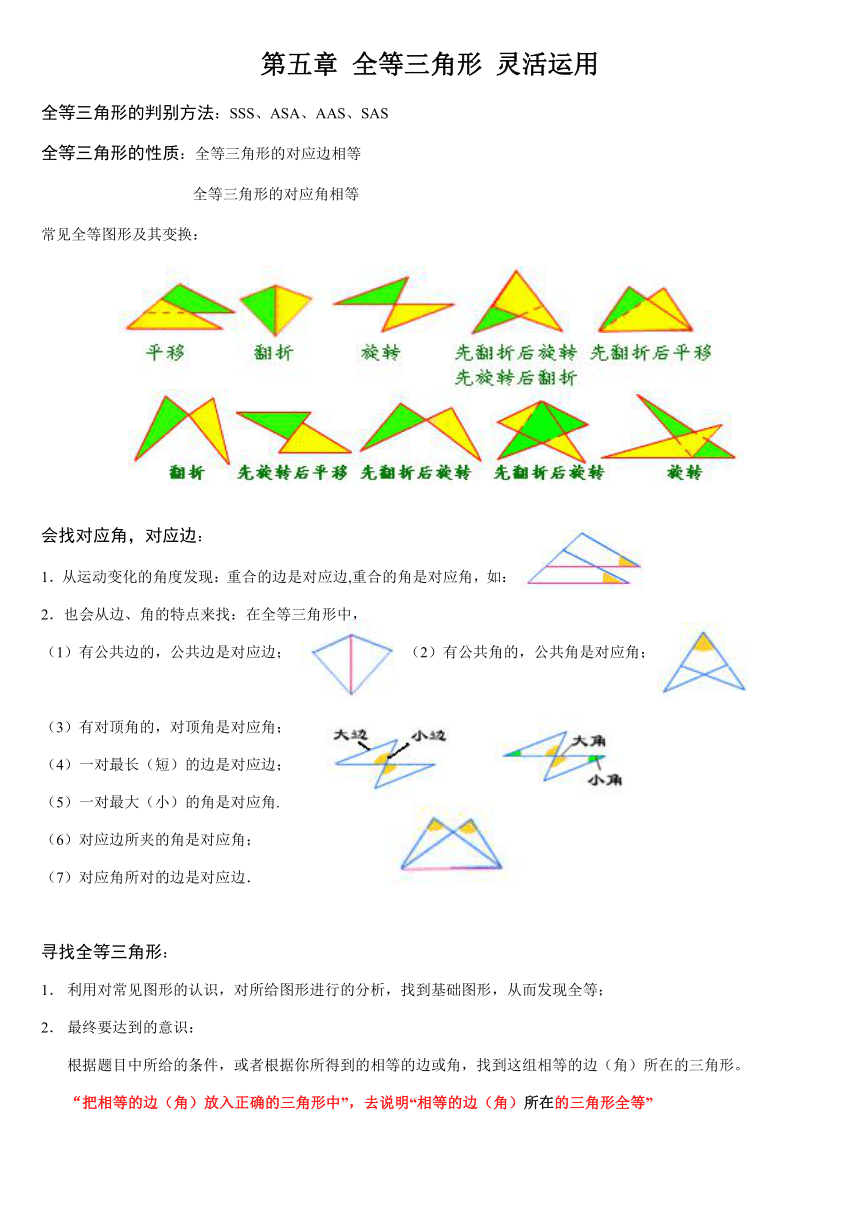
常见全等图形及其变换：
会找对应角，对应边：
1．从运动变化的角度发现：重合的边是对应边,重合的角是对应角，如：
2．也会从边、角的特点来找：在全等三角形中，
（1）有公共边的，公共边是对应边； （2）有公共角的，公共角是对应角；
（3）有对顶角的，对顶角是对应角；
（4）一对最长（短）的边是对应边；
（5）一对最大（小）的角是对应角.
（6）对应边所夹的角是对应角；
（7）对应角所对的边是对应边．
寻找全等三角形：
1． 利用对常见图形的认识，对所给图形进行的分析，找到基础图形，从而发现全等；
2． 最终要达到的意识：
根据题目中所给的条件，或者根据你所得到的相等的边或角，找到这组相等的边（角）所在的三角形。
“把相等的边（角）放入正确的三角形中”，去说明“相等的边（角）所在的三角形全等”
例题讲解：
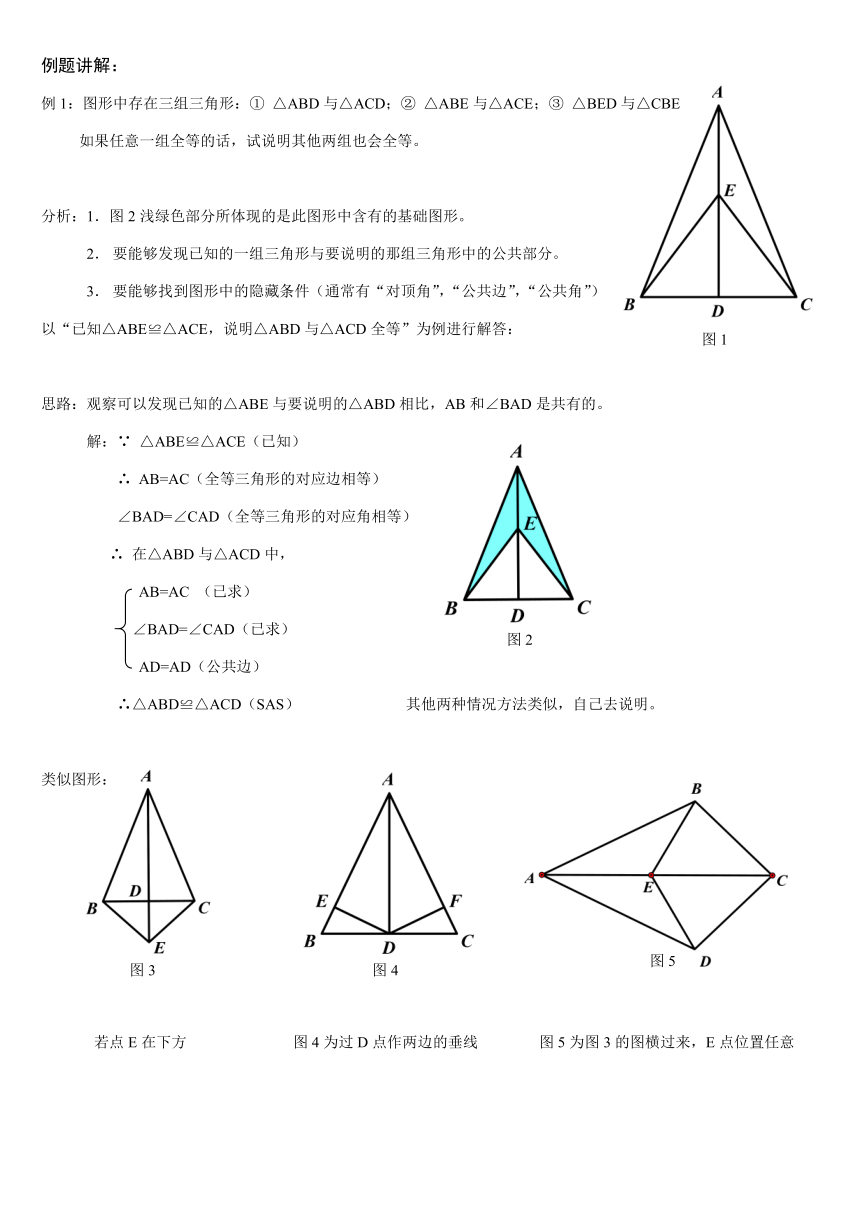
例1：图形中存在三组三角形：① △ABD与△ACD；② △ABE与△ACE；③ △BED与△CBE
如果任意一组全等的话，试说明其他两组也会全等。
分析：1．图2浅绿色部分所体现的是此图形中含有的基础图形。
2． 要能够发现已知的一组三角形与要说明的那组三角形中的公共部分。
3． 要能够找到图形中的隐藏条件（通常有“对顶角”，“公共边”，“公共角”）
以“已知△ABE≌△ACE，说明△ABD与△ACD全等”为例进行解答：
思路：观察可以发现已知的△ABE与要说明的△ABD相比，AB和∠BAD是共有的。
解：∵ △ABE≌△ACE（已知）
∴ AB=AC（全等三角形的对应边相等）
∠BAD=∠CAD（全等三角形的对应角相等）
∴ 在△ABD与△ACD中，
AB=AC （已求）
∠BAD=∠CAD（已求）
AD=AD（公共边）
∴△ABD≌△ACD（SAS） 其他两种情况方法类似，自己去说明。
类似图形：
若点E在下方 图4为过D点作两边的垂线 图5为图3的图横过来，E点位置任意
例2：图6的两三角形全等的话，除了可以得到全等三角形的三组对应角相等，
三组对应边相等之外，还可以由AO=OD，BO=OC，
得到：AO+OC=OD+OB（等式性质）
即：AC=BD
变形：
（1）连接BC，可得到图7，可得到△ABC≌△DCB，
可用SSS、SAS进行说明
（2）延长CD，AB，可得到图8，可得到△ACF≌△DBF
解： ∵ △ABO≌△DCO，
∴ ∠A=∠D（全等三角形的对应角相等）
AO=DO，BO=OC（全等三角形的对应边相等）
∴ AO+OC=OD+OB（等式性质）
即： AC=BD
∴ 在△ACF与△DBF中，
∠F=∠F（公共角）
∠A=∠D（已求）
AC=BD（已求）
∴ △ACF≌△DBF（AAS）
图9，图10为此类型图的不同摆放，具体解题思路相同
结束语：全等三角形的综合运用关键点在于把相等的边（角）
与相对应的三角形对应起来，能够做到根据已有的条件，
再去寻找需要的条件说明全等，然后利用全等三角形的性质，
得到新的边（角）相等，去解决新的问题。
常见基础图形二及其变型：
图2
图1
图4
图5
图3
图6
图7
图8
图9
图10