方程的根与函数的零点2
图片预览




文档简介
课件15张PPT。3.1.1方程的根与函数的零点2、x2-2x-3=0?问题一:判断下列方程是否存在实根思考:方程lnx+2x-6=0是否存在实根?
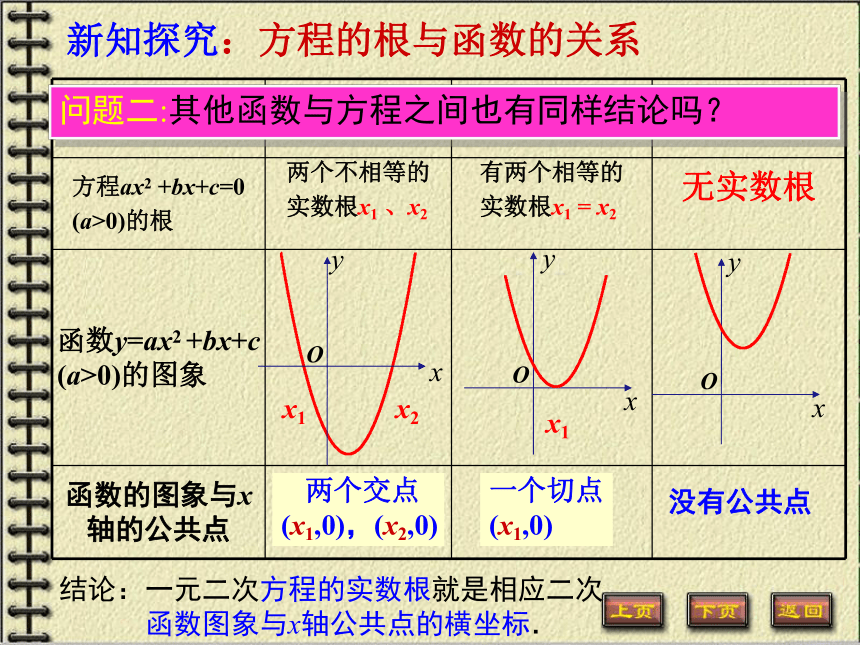
3、x2-2x +m=01、2x-3=0结论:一元二次方程的实数根就是相应二次
函数图象与x轴公共点的横坐标.没有公共点x1x2x1 两个交点
(x1,0),(x2,0)一个切点
(x1,0)问题二:其他函数与方程之间也有同样结论吗?新知探究:方程的根与函数的关系
函数的零点定义:对于函数y=f(x), 使f(x)=0的实数x叫做函数y=f(x)的零点。思考:对于零点,你是如何理解的?如何
求函数的零点??新知探究:方程的根与函数的关系
注:零点不是点而是实数!
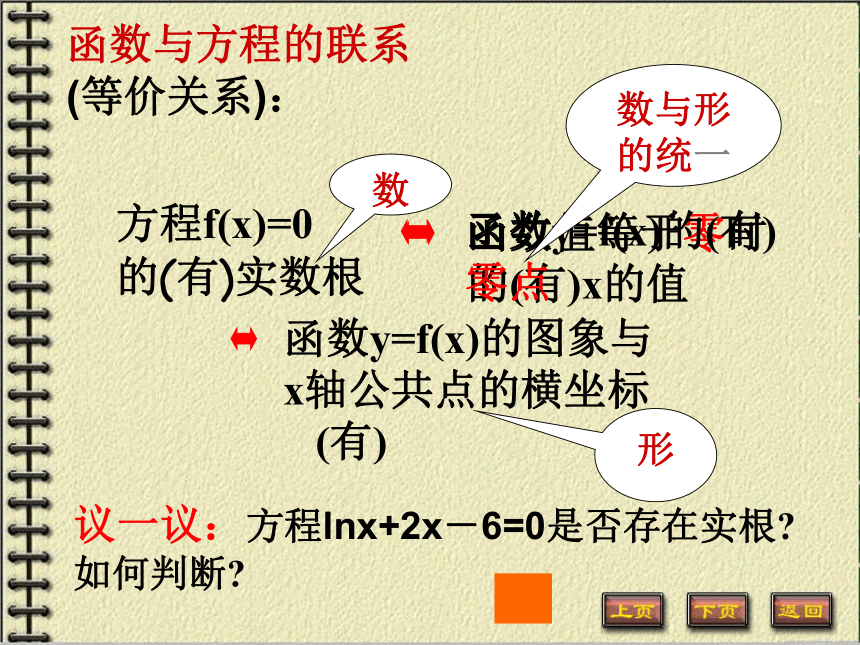
求函数的零点就是求方程的实根.方程f(x)=0
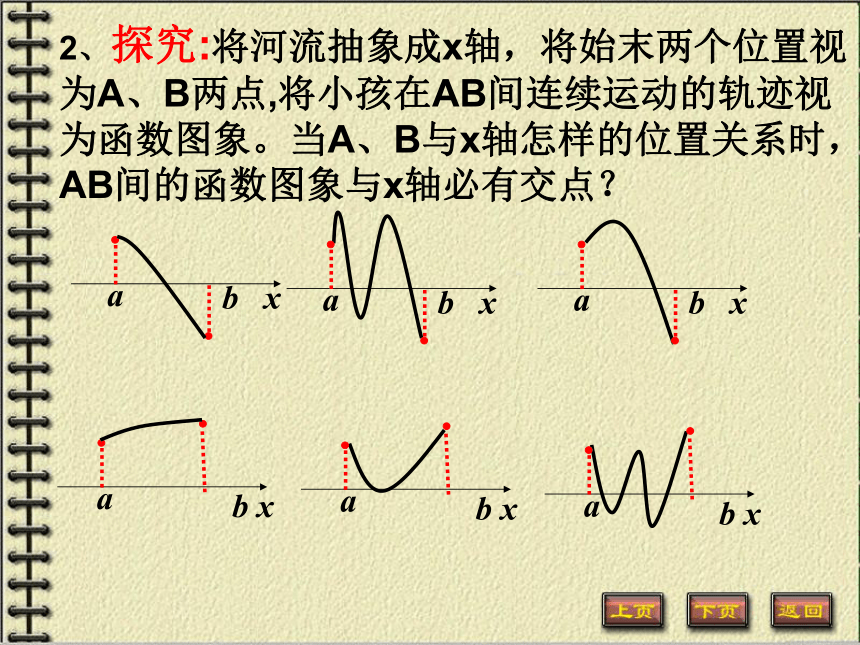
的(有)实数根函数与方程的联系(等价关系):数形数与形的统一议一议:方程lnx+2x-6=0是否存在实根? 如何判断? 定理探究:什么条件下,函数f(x)在(a,b)一定存在零点?2、探究:将河流抽象成x轴,将始末两个位置视为A、B两点,将小孩在AB间连续运动的轨迹视为函数图象。当A、B与x轴怎样的位置关系时,AB间的函数图象与x轴必有交点?定理探究:函数零点存在性定理 :你能找出存在零点的区间吗?
能确定函数零点的个数吗?(1,2) (2,5) (8,9)练一练:( 1)判断函数f(x)=ex-x-3在区间[1,2]上是否存在零点.( 2)已知函数f(x)的图象是连续不断的,且有如下对应关系:辨析2:如果函数y=f(x)在区间[a,b]上连续, f(a)f(b)﹥0,那么函数y=f(x)在区间(a,b)有无零点? 辨析1:如果函数y=f(x)在区间[a,b]上连续,且f(a)f(b)﹤0,那么函数y=f(x)在(a,b)上是否有唯一零点?OxyO反思定理:如果函数y=f(x)在区间[a,b]上
f(a)f(b)﹤0,那么函 数y=f(x)在(a,b)内有零点,即存在c∈ (a,b),使得f(c)=0,这个c也就是方程f(x)=0的根思考:若f(a)f(b)﹤0,则y=f(x)在区间(a,b)上
一定有零点 吗?的图象是连续不断的一条曲线,y辨析3 以下命题对否?由上表和右图可知f(2)<0,f(3)>0,即f(2)·f(3)<0,说明这个函数在区间(2,3)内
有零点。 由于函数f(x)在定义域
(0,+∞)内是增函数,所以
它仅有一个零点。解:用计算器或计算机作出x、f(x)的对应值表和图象-4 -1.30691.09863.38635.60947.79189.945912.079414.1972本节课你在数学知识上和思想方法上分别有何收获?小结与反思作业:课本P88
1(4)、2(2)(3)课后探究:我们已经知道,函数f(x)=lnx+2x-6的唯一零点在
(2,3)内,那么该如何进一步求此零点的值呢?数与形,本是相倚依,焉能分作两边飞。
数缺形时少直觉,形少数时难入微。
数形结合百般好,隔离分家万事非。
切莫忘,几何代数统一体,永远联系,切莫分离!华罗庚谢谢大家!
3、x2-2x +m=01、2x-3=0结论:一元二次方程的实数根就是相应二次
函数图象与x轴公共点的横坐标.没有公共点x1x2x1 两个交点
(x1,0),(x2,0)一个切点
(x1,0)问题二:其他函数与方程之间也有同样结论吗?新知探究:方程的根与函数的关系
函数的零点定义:对于函数y=f(x), 使f(x)=0的实数x叫做函数y=f(x)的零点。思考:对于零点,你是如何理解的?如何
求函数的零点??新知探究:方程的根与函数的关系
注:零点不是点而是实数!
求函数的零点就是求方程的实根.方程f(x)=0
的(有)实数根函数与方程的联系(等价关系):数形数与形的统一议一议:方程lnx+2x-6=0是否存在实根? 如何判断? 定理探究:什么条件下,函数f(x)在(a,b)一定存在零点?2、探究:将河流抽象成x轴,将始末两个位置视为A、B两点,将小孩在AB间连续运动的轨迹视为函数图象。当A、B与x轴怎样的位置关系时,AB间的函数图象与x轴必有交点?定理探究:函数零点存在性定理 :你能找出存在零点的区间吗?
能确定函数零点的个数吗?(1,2) (2,5) (8,9)练一练:( 1)判断函数f(x)=ex-x-3在区间[1,2]上是否存在零点.( 2)已知函数f(x)的图象是连续不断的,且有如下对应关系:辨析2:如果函数y=f(x)在区间[a,b]上连续, f(a)f(b)﹥0,那么函数y=f(x)在区间(a,b)有无零点? 辨析1:如果函数y=f(x)在区间[a,b]上连续,且f(a)f(b)﹤0,那么函数y=f(x)在(a,b)上是否有唯一零点?OxyO反思定理:如果函数y=f(x)在区间[a,b]上
f(a)f(b)﹤0,那么函 数y=f(x)在(a,b)内有零点,即存在c∈ (a,b),使得f(c)=0,这个c也就是方程f(x)=0的根思考:若f(a)f(b)﹤0,则y=f(x)在区间(a,b)上
一定有零点 吗?的图象是连续不断的一条曲线,y辨析3 以下命题对否?由上表和右图可知f(2)<0,f(3)>0,即f(2)·f(3)<0,说明这个函数在区间(2,3)内
有零点。 由于函数f(x)在定义域
(0,+∞)内是增函数,所以
它仅有一个零点。解:用计算器或计算机作出x、f(x)的对应值表和图象-4 -1.30691.09863.38635.60947.79189.945912.079414.1972本节课你在数学知识上和思想方法上分别有何收获?小结与反思作业:课本P88
1(4)、2(2)(3)课后探究:我们已经知道,函数f(x)=lnx+2x-6的唯一零点在
(2,3)内,那么该如何进一步求此零点的值呢?数与形,本是相倚依,焉能分作两边飞。
数缺形时少直觉,形少数时难入微。
数形结合百般好,隔离分家万事非。
切莫忘,几何代数统一体,永远联系,切莫分离!华罗庚谢谢大家!
