北师大版高中数学必修2课件-1.1简单几何体 (共13张PPT)
文档属性
| 名称 | 北师大版高中数学必修2课件-1.1简单几何体 (共13张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 760.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-22 12:41:32 | ||
图片预览



文档简介
(共13张PPT)
1.1 简单几何体
球面:半圆绕其直径旋转所形成的曲面.半圆的圆心叫球心,球心与球面上任一点的连线段叫球的半径,连接球面上两点且过球心的线段叫球的直径.
球体:球面围成的几何体叫球.
探究思考:a.球与球面有什么区别?
b.用一个平面去截球面得到什么图形?其大小有无变化?
c.地球仪上的经线纬线是什么图形?
d.球面上两点间的最短连线是线段吗?
引入新知
看一看
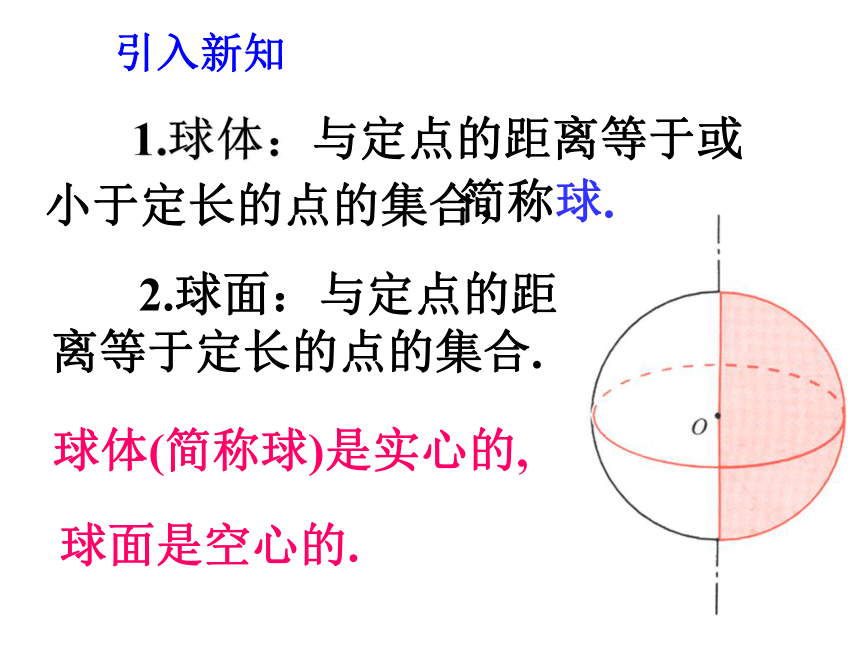
1.球体:与定点的距离等于或小于定长的点的集合,
2.球面:与定点的距离等于定长的点的集合.
球体(简称球)是实心的,
球面是空心的.
简称球.
引入新知
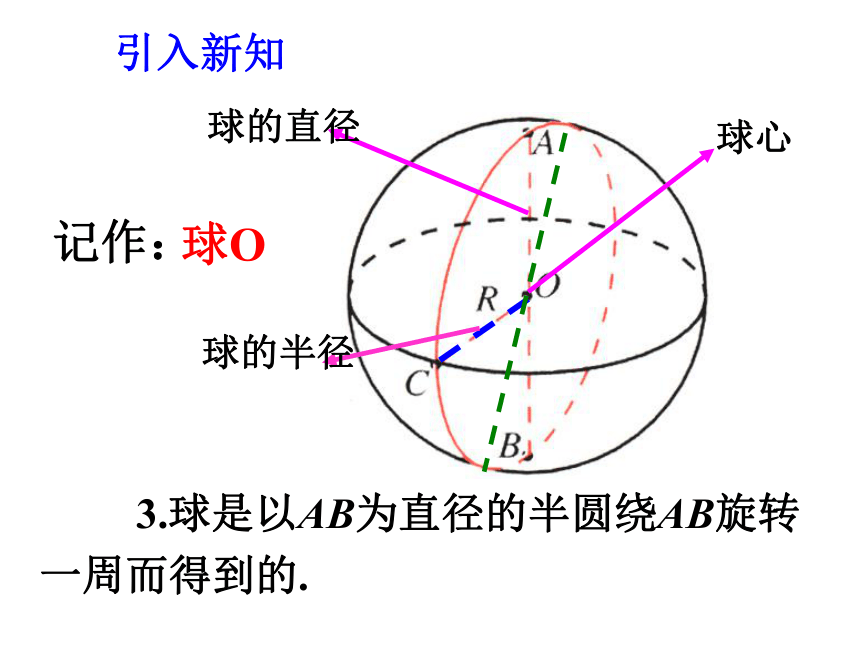
球心
球的半径
球的直径
记作:
球O
3.球是以AB为直径的半圆绕AB旋转一周而得到的.
引入新知
球的截面及其性质
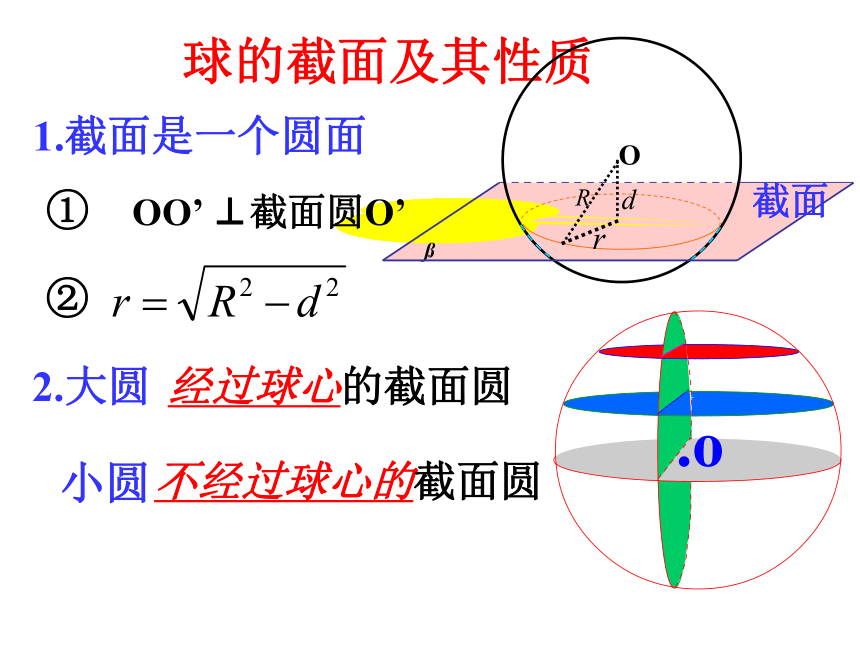
1.截面是一个圆面
O
截面
① OO’ ⊥截面圆O’
②
2.大圆
.o
经过球心的截面圆
小圆
不经过球心的截面圆
旋转面与旋转体
一条平面曲线绕其所在平面上的一定直线旋转形成的曲面叫旋转面.
由封闭的旋转面围成的几何体叫旋转体.
引入新知
圆柱 圆锥 圆台
以矩形的一边所在直线为旋转轴,其余边旋转形成的曲面围成的几何体叫圆柱.
以直角三角形的一直角边所在直线为旋转轴,其余边旋转形成的曲面围成的几何体叫圆锥.
以直角梯形的垂直于底边的腰所在直线为旋转轴,其余边旋转形成的曲面围成的几何体叫圆台.在轴上的这边长度叫高,垂直于轴的边形成底面,不垂直于轴的边形成侧面且无论转到何处,这边都叫侧面的母线.
探究思考:圆柱、圆锥、圆台有何关系?
简单多面体
若干个平面多边形围成的几何体叫简单多面体.
棱柱,棱锥,棱台都是简单多面体.
引入新知
棱柱
棱柱:有两面平行,其余面都是四边形,相邻四边形的公共边都互相平行.
底面:平行的两面.其余各面叫侧面.侧面都是平行四边形.两面的公共边叫棱.两侧面的公共边叫侧棱.侧面与底面多边形的公共顶点叫顶点.夹在两底间的垂直于底的直线段长叫高.
斜棱柱:侧棱不垂直于底的棱柱.直棱柱:侧棱垂直于底的棱柱.正棱柱:侧棱垂直于底且底面是正多边形的棱柱.
按底面边数又可称为三棱柱、四棱柱、五棱柱…
棱锥、棱台
棱锥:一面是多边形,其余面都是有一公共顶点的三角形.多边形叫底面.其余面叫侧面.侧面的公共边叫侧棱.侧面的公共顶点叫棱锥顶点.顶点到底面的垂线段长叫高.底面是正多形,侧面都是全等的三角形的棱锥叫正棱锥.侧面上等腰三角形底边上的高叫斜高.
棱台:用一个平行于底的平面截棱锥,得到的截面与底面间的部分.棱锥的底叫棱台下底,截面叫棱台上底.正棱台:用正棱锥截得的棱台.正棱台的侧面都是全等的等腰梯形,其高叫正棱台的斜高.
棱柱
棱锥
A
B
C
D
E
A’
B’
C’
D’
E’
S
A
B
C
D
定
义
有两个面相互平行,其余各面都是四边形,并且每相邻两个四边形的公共边都相互平行,由这些面所围成的几何体叫作棱柱.
有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫作棱锥
表示方法
棱柱ABCDE-A’B’C’D’E’,
棱柱AC’.
棱锥S-ABCD, 棱锥S-AC.
分
类
以边数分类.如四棱柱,五棱柱.
以底面是n边形,(n>2).如三棱锥,四棱锥.
2 以侧棱与底面的位置关系.如斜棱柱,直棱柱,正棱柱.
2 正棱锥,非正棱锥.
正棱柱
正棱锥
A
B
C
D
E
A’
B’
C’
D’
E’
定义
底面是正多边形的直棱柱叫作正棱柱.
如果一个棱锥的底面是正多边形,并各侧面全等,这样的棱锥叫作正棱锥.
性
质
1 侧棱相等,侧面是矩形.
2 两个底面与平行于底面的截面是全等的多边形.
3 过不相邻的两条侧棱的截面是矩形.
1.各侧棱相等,各侧面都是全等的等腰三角形.各等腰三角形底边上的高相等,它叫作正棱锥的斜高.
2.棱锥的高、斜高和斜高在底面的射影组成一个直角三角形;棱锥的高、侧棱和侧棱在底面内的射影也组成一个直角三角形.
1.1 简单几何体
球面:半圆绕其直径旋转所形成的曲面.半圆的圆心叫球心,球心与球面上任一点的连线段叫球的半径,连接球面上两点且过球心的线段叫球的直径.
球体:球面围成的几何体叫球.
探究思考:a.球与球面有什么区别?
b.用一个平面去截球面得到什么图形?其大小有无变化?
c.地球仪上的经线纬线是什么图形?
d.球面上两点间的最短连线是线段吗?
引入新知
看一看
1.球体:与定点的距离等于或小于定长的点的集合,
2.球面:与定点的距离等于定长的点的集合.
球体(简称球)是实心的,
球面是空心的.
简称球.
引入新知
球心
球的半径
球的直径
记作:
球O
3.球是以AB为直径的半圆绕AB旋转一周而得到的.
引入新知
球的截面及其性质
1.截面是一个圆面
O
截面
① OO’ ⊥截面圆O’
②
2.大圆
.o
经过球心的截面圆
小圆
不经过球心的截面圆
旋转面与旋转体
一条平面曲线绕其所在平面上的一定直线旋转形成的曲面叫旋转面.
由封闭的旋转面围成的几何体叫旋转体.
引入新知
圆柱 圆锥 圆台
以矩形的一边所在直线为旋转轴,其余边旋转形成的曲面围成的几何体叫圆柱.
以直角三角形的一直角边所在直线为旋转轴,其余边旋转形成的曲面围成的几何体叫圆锥.
以直角梯形的垂直于底边的腰所在直线为旋转轴,其余边旋转形成的曲面围成的几何体叫圆台.在轴上的这边长度叫高,垂直于轴的边形成底面,不垂直于轴的边形成侧面且无论转到何处,这边都叫侧面的母线.
探究思考:圆柱、圆锥、圆台有何关系?
简单多面体
若干个平面多边形围成的几何体叫简单多面体.
棱柱,棱锥,棱台都是简单多面体.
引入新知
棱柱
棱柱:有两面平行,其余面都是四边形,相邻四边形的公共边都互相平行.
底面:平行的两面.其余各面叫侧面.侧面都是平行四边形.两面的公共边叫棱.两侧面的公共边叫侧棱.侧面与底面多边形的公共顶点叫顶点.夹在两底间的垂直于底的直线段长叫高.
斜棱柱:侧棱不垂直于底的棱柱.直棱柱:侧棱垂直于底的棱柱.正棱柱:侧棱垂直于底且底面是正多边形的棱柱.
按底面边数又可称为三棱柱、四棱柱、五棱柱…
棱锥、棱台
棱锥:一面是多边形,其余面都是有一公共顶点的三角形.多边形叫底面.其余面叫侧面.侧面的公共边叫侧棱.侧面的公共顶点叫棱锥顶点.顶点到底面的垂线段长叫高.底面是正多形,侧面都是全等的三角形的棱锥叫正棱锥.侧面上等腰三角形底边上的高叫斜高.
棱台:用一个平行于底的平面截棱锥,得到的截面与底面间的部分.棱锥的底叫棱台下底,截面叫棱台上底.正棱台:用正棱锥截得的棱台.正棱台的侧面都是全等的等腰梯形,其高叫正棱台的斜高.
棱柱
棱锥
A
B
C
D
E
A’
B’
C’
D’
E’
S
A
B
C
D
定
义
有两个面相互平行,其余各面都是四边形,并且每相邻两个四边形的公共边都相互平行,由这些面所围成的几何体叫作棱柱.
有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫作棱锥
表示方法
棱柱ABCDE-A’B’C’D’E’,
棱柱AC’.
棱锥S-ABCD, 棱锥S-AC.
分
类
以边数分类.如四棱柱,五棱柱.
以底面是n边形,(n>2).如三棱锥,四棱锥.
2 以侧棱与底面的位置关系.如斜棱柱,直棱柱,正棱柱.
2 正棱锥,非正棱锥.
正棱柱
正棱锥
A
B
C
D
E
A’
B’
C’
D’
E’
定义
底面是正多边形的直棱柱叫作正棱柱.
如果一个棱锥的底面是正多边形,并各侧面全等,这样的棱锥叫作正棱锥.
性
质
1 侧棱相等,侧面是矩形.
2 两个底面与平行于底面的截面是全等的多边形.
3 过不相邻的两条侧棱的截面是矩形.
1.各侧棱相等,各侧面都是全等的等腰三角形.各等腰三角形底边上的高相等,它叫作正棱锥的斜高.
2.棱锥的高、斜高和斜高在底面的射影组成一个直角三角形;棱锥的高、侧棱和侧棱在底面内的射影也组成一个直角三角形.
