北师大版高中数学必修2课件-1.4.1 空间图形基本关系的认识 (共21张PPT)
文档属性
| 名称 | 北师大版高中数学必修2课件-1.4.1 空间图形基本关系的认识 (共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 580.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-22 12:44:31 | ||
图片预览




文档简介
课件21张PPT。1.4.1 空间图形基本
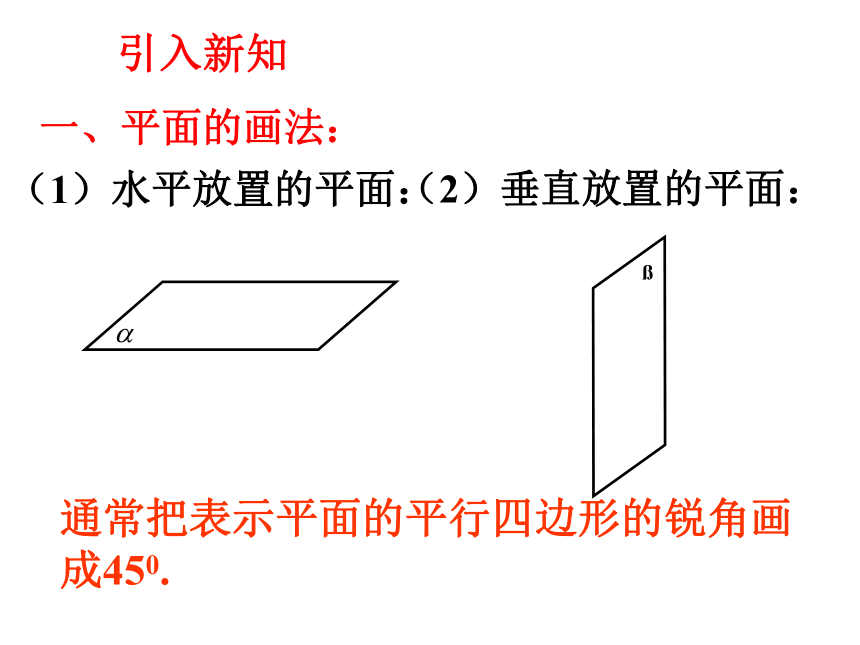
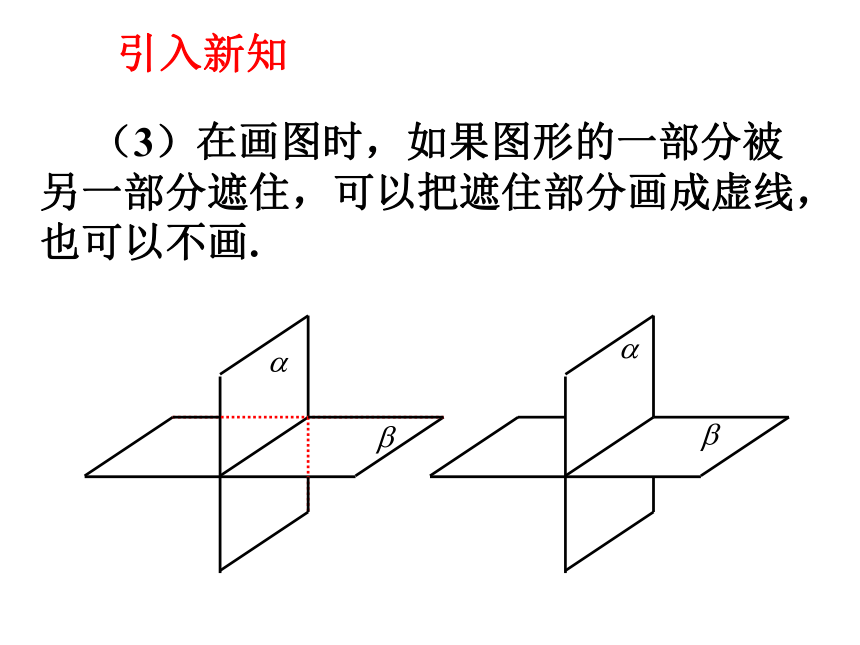
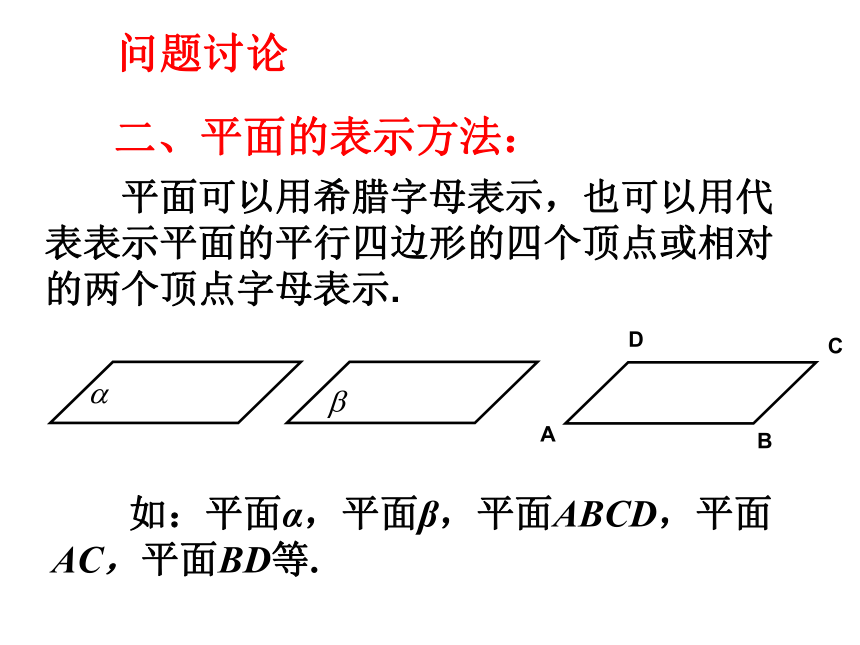
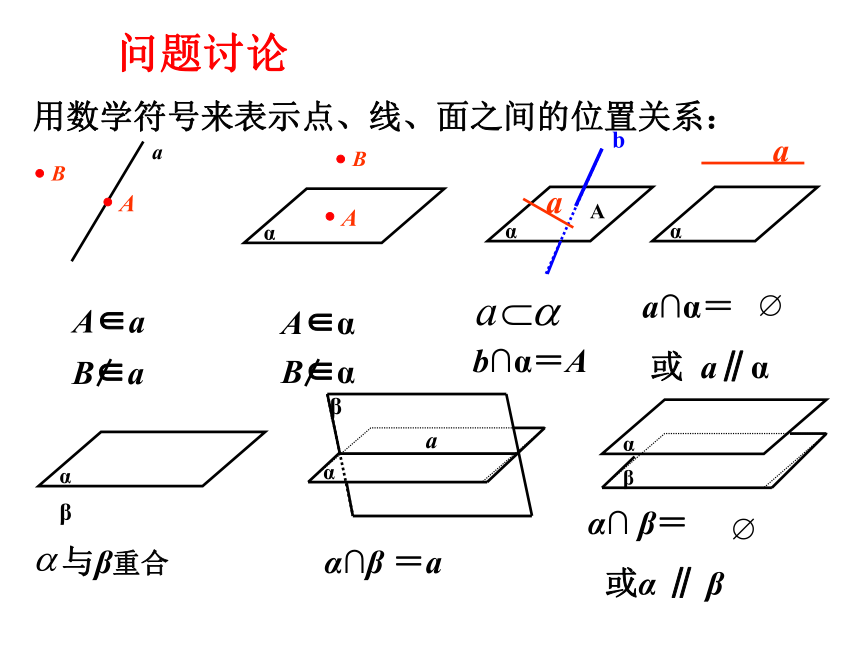
关系的认识一、平面的画法:(1)水平放置的平面:(2)垂直放置的平面:通常把表示平面的平行四边形的锐角画成450.引入新知 (3)在画图时,如果图形的一部分被另一部分遮住,可以把遮住部分画成虚线,也可以不画.引入新知二、平面的表示方法: 平面可以用希腊字母表示,也可以用代表表示平面的平行四边形的四个顶点或相对的两个顶点字母表示. 如:平面α,平面β,平面ABCD,平面AC,平面BD等.问题讨论三、用数学符号来表示点、线、面之间的位置关系: 点A在直线a上:记为:A∈a点B不在直线a上: 点A在平面α上:记为:A∈α点B不在平面α上:(1)空间点与直线的位置关系:(2)空间点与平面的位置关系:问题讨论(3)空间直线与平面的位置关系: 直线a上的所有点都在平面α上,称直线a在平面α内,或称平面α通过直线a.记为: 直线a与平面α只有一个公共点A时,称直线a与平面α相交. 记为:a∩α=A 直线a与平面α没有公共点时,称直线a与平面α平行. 记为:a∩α= 或 a∥α.问题讨论(4)空间平面与平面的位置关系: 当平面α上的所有点都在平面β上时,称平面α与平面β重合. 当两个不同平面α与平面β有公共点时,它们的公共点组成集合a,称平面α与平面β相交. 记做: α∩ β=a. 当平面α与平面β没有公共点时,称平面α与平面β平行.记做: α∩ β= 或α ∥ β.问题讨论用数学符号来表示点、线、面之间的位置关系:A∈aA∈αb∩α=Aa∩α=
或 a∥αα∩β =aα∩ β=
或α ∥ β 与β重合问题讨论(5)空间直线与直线的位置关系:问题1: 在平面几何中,两直线的位置关系如何?问题2:没有公共点的直线一定平行吗?
问题3:没有公共点的两直线一定在同一平面内吗?空间两直线的位置关系及判断问题讨论定义 不同在任何一个平面内的两
条直线叫作异面直线.没有只有一个没有共面不共面共面引入新知⒈ 异面直线:不同在任何一个平面内的两条直线.异面直线异面直线 如图所示:正方体的棱所在的直线中,与直线A1B异面的有哪些? 答案:D1C1、C1C、CDD1D、AD、B1C1议 一 议异面直线直观图的画法两条直线异面:引入新知异面直线直观图的画法分别在两个相交平面内的两条异面直线:引入新知 巩固:①画两个相交平面,在这两个平面内
各画一条直线,使它们成为:⑴平行直线 ;⑵相
交直线; ⑶异面直线.复习巩固两条异面直线指:A.空间中不相交的两条直线;
B.某平面内的一条直线和这平面外的直线;
C.分别在不同平面内的两条直线;
D.不在同一平面内的两条直线;
E.不同在任一平面内的两条直线;
F.分别在两个不同平面内的两条直线;
G.某一平面内的一条直线和这个平面外的一条直线;
H.空间没有公共点的两条直线;
I.既不相交,又不平行的两条直线. 复习巩固空间两直线的位置关系:结论:不同在任何一个平面内的两条直线为异面直线空间两条直线的位置关系:相交、平行、异面⑴空间两条直线的位置关系归纳为:复习巩固 例1.把下列语句用集合符号表示,并画出直观图.
(1)点A在平面α内,点B不在平面α内,点A,B
都在直线 a上;
(2)平面α与平面β相交于直线 m,直线 a 在平
面α内且平行于直线 m.例题解析例2.把下列图形中的点、线、面关系用集合符号表示出来.例题解析
关系的认识一、平面的画法:(1)水平放置的平面:(2)垂直放置的平面:通常把表示平面的平行四边形的锐角画成450.引入新知 (3)在画图时,如果图形的一部分被另一部分遮住,可以把遮住部分画成虚线,也可以不画.引入新知二、平面的表示方法: 平面可以用希腊字母表示,也可以用代表表示平面的平行四边形的四个顶点或相对的两个顶点字母表示. 如:平面α,平面β,平面ABCD,平面AC,平面BD等.问题讨论三、用数学符号来表示点、线、面之间的位置关系: 点A在直线a上:记为:A∈a点B不在直线a上: 点A在平面α上:记为:A∈α点B不在平面α上:(1)空间点与直线的位置关系:(2)空间点与平面的位置关系:问题讨论(3)空间直线与平面的位置关系: 直线a上的所有点都在平面α上,称直线a在平面α内,或称平面α通过直线a.记为: 直线a与平面α只有一个公共点A时,称直线a与平面α相交. 记为:a∩α=A 直线a与平面α没有公共点时,称直线a与平面α平行. 记为:a∩α= 或 a∥α.问题讨论(4)空间平面与平面的位置关系: 当平面α上的所有点都在平面β上时,称平面α与平面β重合. 当两个不同平面α与平面β有公共点时,它们的公共点组成集合a,称平面α与平面β相交. 记做: α∩ β=a. 当平面α与平面β没有公共点时,称平面α与平面β平行.记做: α∩ β= 或α ∥ β.问题讨论用数学符号来表示点、线、面之间的位置关系:A∈aA∈αb∩α=Aa∩α=
或 a∥αα∩β =aα∩ β=
或α ∥ β 与β重合问题讨论(5)空间直线与直线的位置关系:问题1: 在平面几何中,两直线的位置关系如何?问题2:没有公共点的直线一定平行吗?
问题3:没有公共点的两直线一定在同一平面内吗?空间两直线的位置关系及判断问题讨论定义 不同在任何一个平面内的两
条直线叫作异面直线.没有只有一个没有共面不共面共面引入新知⒈ 异面直线:不同在任何一个平面内的两条直线.异面直线异面直线 如图所示:正方体的棱所在的直线中,与直线A1B异面的有哪些? 答案:D1C1、C1C、CDD1D、AD、B1C1议 一 议异面直线直观图的画法两条直线异面:引入新知异面直线直观图的画法分别在两个相交平面内的两条异面直线:引入新知 巩固:①画两个相交平面,在这两个平面内
各画一条直线,使它们成为:⑴平行直线 ;⑵相
交直线; ⑶异面直线.复习巩固两条异面直线指:A.空间中不相交的两条直线;
B.某平面内的一条直线和这平面外的直线;
C.分别在不同平面内的两条直线;
D.不在同一平面内的两条直线;
E.不同在任一平面内的两条直线;
F.分别在两个不同平面内的两条直线;
G.某一平面内的一条直线和这个平面外的一条直线;
H.空间没有公共点的两条直线;
I.既不相交,又不平行的两条直线. 复习巩固空间两直线的位置关系:结论:不同在任何一个平面内的两条直线为异面直线空间两条直线的位置关系:相交、平行、异面⑴空间两条直线的位置关系归纳为:复习巩固 例1.把下列语句用集合符号表示,并画出直观图.
(1)点A在平面α内,点B不在平面α内,点A,B
都在直线 a上;
(2)平面α与平面β相交于直线 m,直线 a 在平
面α内且平行于直线 m.例题解析例2.把下列图形中的点、线、面关系用集合符号表示出来.例题解析
