针对性训练-----几何探究题

针对性训练-----几何探究题
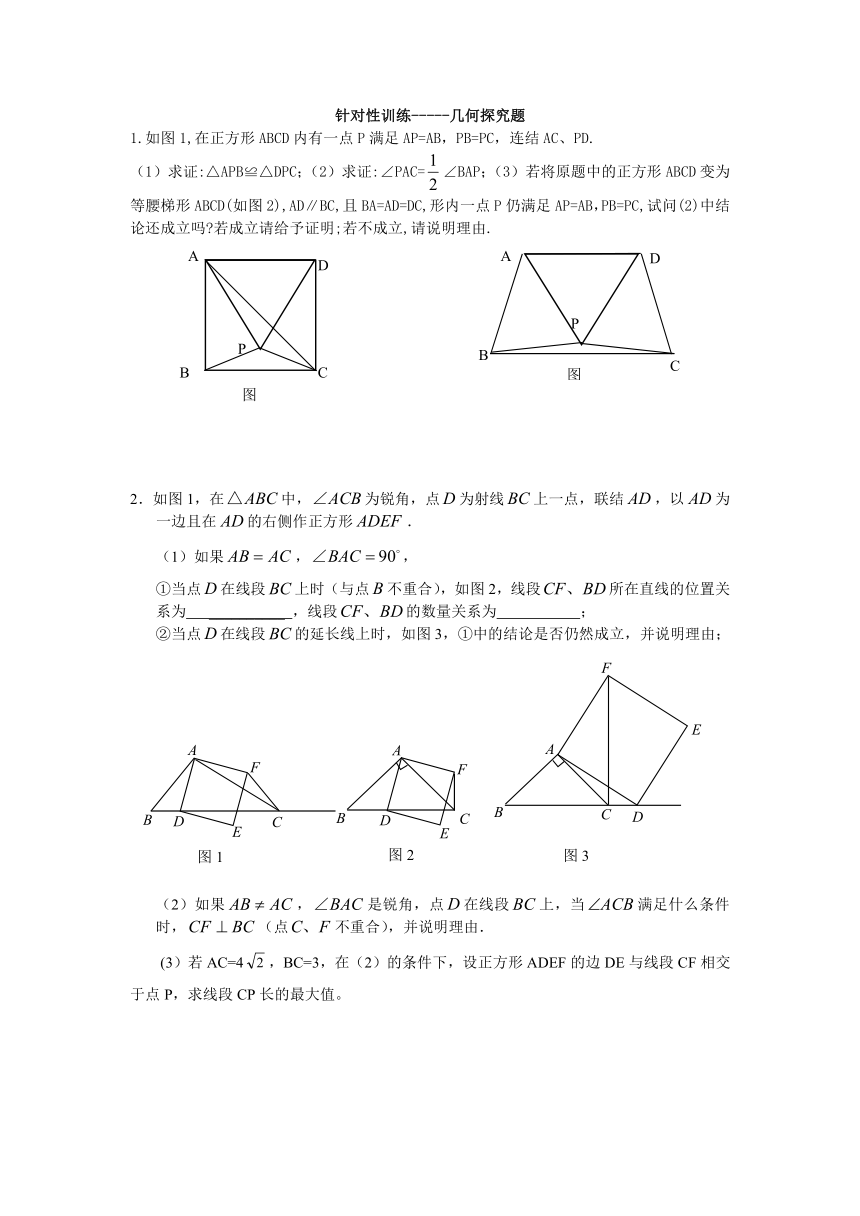
1.如图1,在正方形ABCD内有一点P满足AP=AB，PB=PC，连结AC、PD.
（1）求证:△APB≌△DPC；（2）求证:∠PAC=∠BAP；（3）若将原题中的正方形ABCD变为等腰梯形ABCD(如图2),AD∥BC,且BA=AD=DC,形内一点P仍满足AP=AB，PB=PC,试问(2)中结论还成立吗 若成立请给予证明;若不成立,请说明理由.
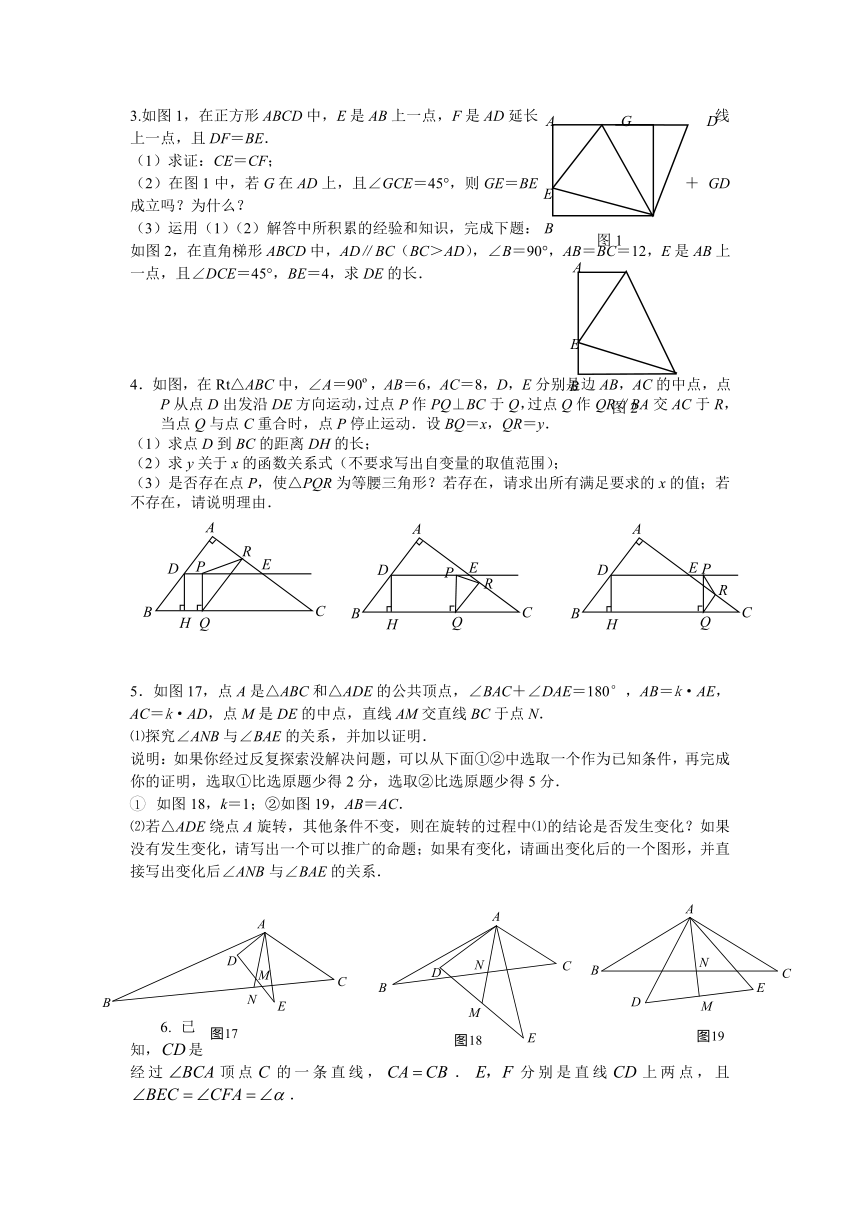
2．如图1，在中，为锐角，点为射线上一点，联结，以为一边且在的右侧作正方形．
（1）如果，，
①当点在线段上时（与点不重合），如图2，线段所在直线的位置关系为 __________ ，线段的数量关系为 ；
②当点在线段的延长线上时，如图3，①中的结论是否仍然成立，并说明理由；
（2）如果，是锐角，点在线段上，当满足什么条件时，（点不重合），并说明理由．
(3）若AC=4，BC=3，在（2）的条件下，设正方形ADEF的边DE与线段CF相交于点P，求线段CP长的最大值。
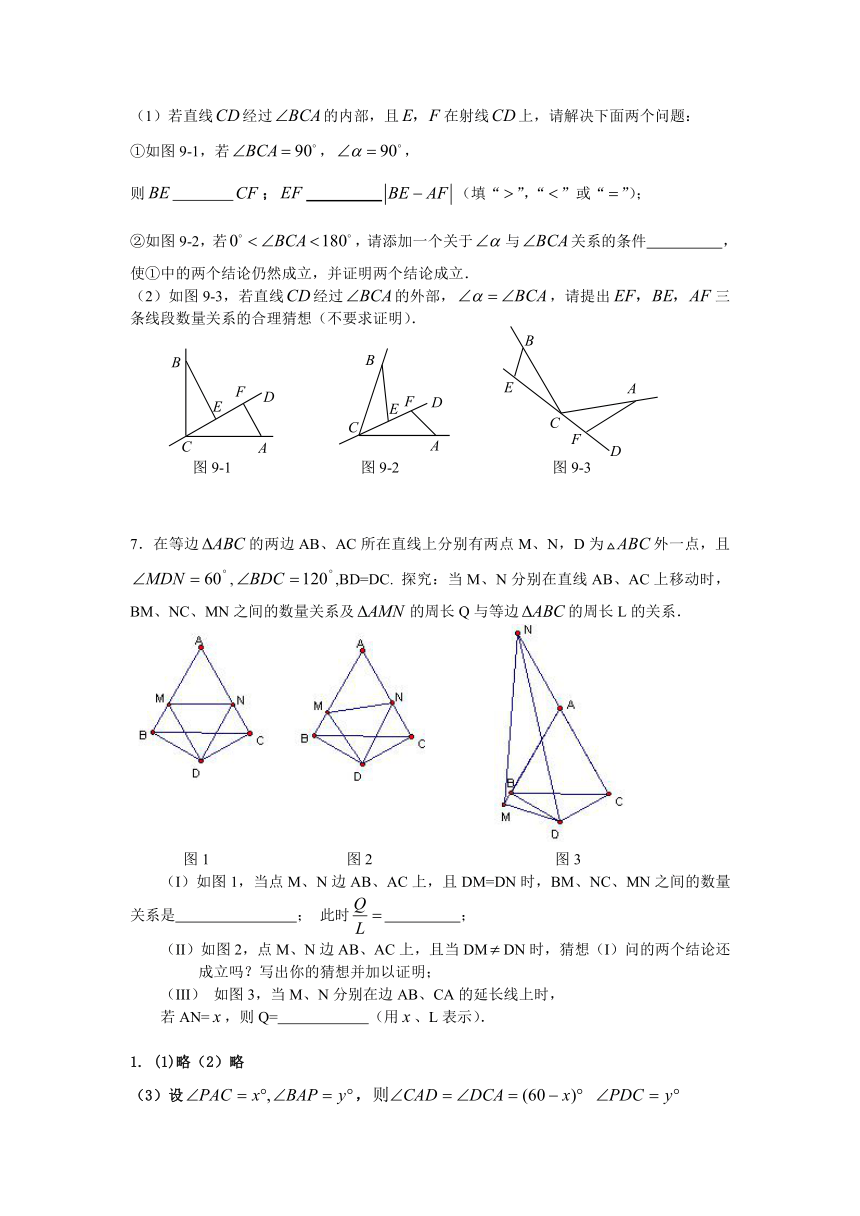
3.如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE．
（1）求证：CE＝CF；
（2）在图1中，若G在AD上，且∠GCE＝45°，则GE＝BE＋GD成立吗？为什么？
（3）运用（1）（2）解答中所积累的经验和知识，完成下题：
如图2，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC＝12，E是AB上一点，且∠DCE＝45°，BE＝4，求DE的长．
4．如图，在Rt△ABC中，∠A＝90 ，AB＝6，AC＝8，D，E分别是边AB，AC的中点，点P从点D出发沿DE方向运动，过点P作PQ⊥BC于Q，过点Q作QR∥BA交AC于R，当点Q与点C重合时，点P停止运动．设BQ＝x，QR＝y．
（1）求点D到BC的距离DH的长；
（2）求y关于x的函数关系式（不要求写出自变量的取值范围）；
（3）是否存在点P，使△PQR为等腰三角形？若存在，请求出所有满足要求的x的值；若不存在，请说明理由．
5．如图17，点A是△ABC和△ADE的公共顶点，∠BAC＋∠DAE＝180°，AB＝k·AE，AC＝k·AD，点M是DE的中点，直线AM交直线BC于点N．
⑴探究∠ANB与∠BAE的关系，并加以证明．
说明：如果你经过反复探索没解决问题，可以从下面①②中选取一个作为已知条件，再完成你的证明，选取①比选原题少得2分，选取②比选原题少得5分．
1 如图18，k＝1；②如图19，AB＝AC．
⑵若△ADE绕点A旋转，其他条件不变，则在旋转的过程中⑴的结论是否发生变化？如果没有发生变化，请写出一个可以推广的命题；如果有变化，请画出变化后的一个图形，并直接写出变化后∠ANB与∠BAE的关系．
6.已知，是经过顶点的一条直线，．分别是直线上两点，且．
（1）若直线经过的内部，且在射线上，请解决下面两个问题：
①如图9-1，若，，
则 ； （填“”，“”或“”）；
②如图9-2，若，请添加一个关于与关系的条件 ，使①中的两个结论仍然成立，并证明两个结论成立．
（2）如图9-3，若直线经过的外部，，请提出三条线段数量关系的合理猜想（不要求证明）．
7．在等边的两边AB、AC所在直线上分别有两点M、N，D为外一点，且,,BD=DC. 探究：当M、N分别在直线AB、AC上移动时，BM、NC、MN之间的数量关系及的周长Q与等边的周长L的关系．
图1 图2 图3
（I）如图1，当点M、N边AB、AC上，且DM=DN时，BM、NC、MN之间的数量关系是 ； 此时 ；
（II）如图2，点M、N边AB、AC上，且当DMDN时，猜想（I）问的两个结论还成立吗？写出你的猜想并加以证明；
（III） 如图3，当M、N分别在边AB、CA的延长线上时，
若AN=，则Q= （用、L表示）．
1. (1)略（2）略
（3）设，
得即
2．（1）①垂直，相等；……………1分
②当点D在BC的延长线上时①的结论仍成立．………………2分
由正方形ADEF得 AD＝AF ，∠DAF＝90 ．
∵∠BAC＝90 ，∴∠DAF＝∠BAC ， ∴∠DAB＝∠FAC，
又AB＝AC ，∴△DAB≌△FAC ，
∴CF＝BD ， ∠ACF＝∠ABD．
∵∠BAC＝90 ， AB＝AC ，
∴∠ABC＝45 ，∴∠ACF＝45 ，
∴∠BCF＝∠ACB+∠ACF＝90 ． 即 CF⊥BD.…………5分
（2）当∠ACB＝45 时，CF⊥BD（如图）． …………6分
理由：过点A作AG⊥AC交CB或CB的延长线于点G，
则∠GAC＝90 ， ∵∠ACB＝45°,∠AGC＝90°—∠ACB＝45°，
∴∠ACB＝∠AGC，∴AC＝AG，
∵点D在线段BC上，∴点D在线段GC上，由（1）①可知CF⊥BD. …7分
（3）如图：作AQBC于Q ∵∠ACB=45° AC=4 ∴CQ=AQ=4
∵∠PCD=∠ADP=90°∴∠ADQ+∠CDP=∠CDP+∠CPD=90°
∴△ADQ∽△DPC ∴=
设CD为x（0＜x＜3）则DQ=CQ－CD=4－x 则=
∴PC=(－x2+4x)=－(x－2)2+1≥1 当x=2时，PC最长，此时PC=1
3.（1）证明：如图1，在正方形ABCD中，
∵BC＝CD，∠B＝∠CDF，BE＝DF，
∴△CBE≌△CDF． ∴CE＝CF．…….3分
（2）GE＝BE＋GD成立．理由是：
∵△CBE≌△CDF， ∴∠BCE＝∠DCF．
∴∠BCE＋∠ECD＝∠DCF＋∠ECD
即∠ECF＝∠BCD＝90°， 又∠GCE＝45°，
∴∠GCF＝∠GCE＝45°．
∵CE＝CF，∠GCE＝∠GCF，GC＝GC，
∴△ECG≌△FCG． ……..4分
∴GE＝GF ∴GE＝DF＋GD＝BE＋GD．…..5分
（3）解：过C作CG⊥AD，交AD延长线于G．
在直角梯形ABCD中，∵AD∥BC ∴∠A＝∠B＝90°．
又∠CGA＝90°，AB＝BC， ∴四边形ABCG 为正方形． ………6分
∴AG＝BC＝12． 已知∠DCE＝45°，根据（1）（2）可知，ED＝BE＋DG．.. 7分
设DE＝x，则DG＝x－4， ∴AD＝AG－DG=12－（x－4）=16－x．
在Rt△AED中， ∵，即．
解这个方程，得：x＝10． ∴DE＝10．
4.（1），，，． 点为中点，．，． ，
，．---------------2分
（2），． ，，
，，即关于的函数关系式为：． -------5分
（3）存在，分三种情况：
①当时，过点作于，则．
，，．
，，
，． --------8分
②当时，， ． -------10分
③当时，则为中垂线上的点，
于是点为的中点，．
，，． -----13分
综上所述，当为或6或时，为等腰三角形． -----14分
5．（1）∠ANB+∠BAE=180 ．……1分
证明：（法一）如图1，延长AN到F，使MF=AM，连接DF、EF. ………………2分
∵点M是DE 的中点，∴DM=ME， ∴四边形ADFE是平行四边形 ，……………3分
∴AD∥EF，AD=EF， ∴∠DAE+∠AEF =180 ， ∵∠BAC+∠DAE=180 ，
∴∠BAC=∠AEF ，………4分 ∵AB=kAE，AC=kAD，
∴， ∴……6分
∴△ABC∽△EAF ∴∠B=∠EAF …………8分
∵∠ANB+∠B+∠BAF =180 ∴∠ANB+∠EAF+∠BAF =180
即∠ANB+∠BAE=180 ，…………10分
（法二）如图2，延长DA到F，使AF=AD，连接EF.………2分
∵∠BAC+∠DAE=180 ，∠DAE +∠EAF =180 ，
∴∠BAC=∠EAF，………………3分 ∵AB=kAE，AC=kAD，
∴， ∴，………4分
∴△ABC∽△AEF，………5分
∴∠B=∠AEF，………6分 ∵点M是DE 的中点，∴DM=ME，
又∵AF=AD， ∴AM是△DEF的中位线，
∴AM∥EF，……7分 ∴∠NAE=∠AEF，
∴∠B=∠NAE，……8分 ∵∠ANB+∠B+∠BAN=180 ，
∴∠ANB+∠NAE+∠BAN =180 ，
即∠ANB+∠BAE=180 ．………10分
(2)变化．如图3（仅供参考），∠ANB=∠BAE．……12分
选取（ⅰ），如图4.
证明：延长AM到F，使MF=AM，连接DF、EF.
∵点M是DE的中点，∴DM=ME
∴四边形ADFE是平行四边形，…………4分
∴AD∥FE，AD=EF， ∴∠DAE+∠AEF =180 ，
∵∠BAC+∠DAE=180 ， ∴∠BAC=∠DAE， ………6分
∵AB=kAE，AC=kAD，， ∴AB=AE ，AC=AD，
∴AC=EF，……7分 ∴△ABC≌△EAF， ∴∠B=∠EAF， …8分
∵∠ANB+∠B+∠BAF=180 ， ∴∠ANB+∠EAF+∠BAF=180 ，
即∠ANB+∠BAE=180 ．……10分
选取（ⅱ），如图5.
证明：∵AB=AC，∴∠B=（180 -∠BAC），…………3分
∵∠BAC+∠DAE=180 ， ∴∠DAE=180 -∠BAC，
∴∠B=∠DAE， ∵AB=kAE，AC=kAD，
∴AE=AD， ∵AM是△ADE的中线，AB=AC，
∴∠EAM=∠DAE， ∴∠B=∠EAM，………4分
∵∠ANB+∠B+∠BAM=180 ， ∴∠ANB+∠EAM +∠BAM=180 ，
即∠ANB+∠BAE=180 ．…5分
6.（1）①；； 2分 ②所填的条件是：． 4分
证明：在中，．
，．
又，．
又，， ．
，． 又，． 7分
（2）．
7.（I）如图1， BM、NC、MN之间的数量关系 BM+NC=MN ．此时 ．
（II）猜想：结论仍然成立．
证明：如图，延长AC至E，使CE=BM，连接DE．
,且．．
又是等边三角形，．
在与中：
(SAS) ．DM=DE,
在与中：
(SAS) MN=NE=NC+BM
的周长Q=AM+AN+MN=AB+AC =2AB
而等边的周长L=3AB .
（III）如图3，当M、N分别在AB、CA的延长线上时，若AN=，
则Q=2+（用、L表示）．
8.如图24－1，正方形ABCD和正方形QMNP， M是正方形ABCD的对称中心，MN交AB于F，QM交AD于E．
（1）猜想：ME 与MF的数量关系
（2）如图24－2，若将原题中的“正方形”改为“菱形”，且∠M =∠B，其它条件不变，探索线段ME与线段MF的数量关系，并加以证明．
（3）如图24－3，若将原题中的“正方形”改为“矩形”，且AB:BC=1:2，其它条件不变，探索线段ME与线段MF的数量关系，并说明理由．
（4）如图24－4，若将原题中的“正方形”改为平行四边形，且∠M =∠B ，
AB:BC = m，其它条件不变，求出ME：MF的值。（直接写出答案）
8.（1）ME=MF ……………1分 （2）ME=MF． ………… 2分
证明：过点M作MH⊥AD于H，MG⊥AB于G，连结AM．
∵M是菱形ABCD的对称中心，∴O是菱形ABCD对角线的交点，
∴AM平分∠BAD，∴MH=MG
∵∠M=∠B，∴∠M+∠BAD=180 ，又∠MHA=∠MGF=90 ，
∴∠HMG+∠BAD=180 ．∴∠EMF=∠HMG，
∴∠EMH=∠FMG．∵∠MHE=∠MGF，
∴△MHE≌△MGF，∴ME=MF．……4分
（3）ME:MF=1:2．…………………………5分
证明：过点M作MH⊥AD于H，MG⊥AB于G，
∵∠M=∠B，∴∠A=∠EMF=90 ，又∵∠MHA=∠MGA=90 ，
∴∠HMG=90 ．∴∠EMF=∠HMG，∴∠EMH=∠FMG．
∵∠MHE=∠MGF，∴△MHE∽△MGF
，∴． --------6分
又∵M是矩形ABCD的对称中心，∴O是矩形ABCD对角线的中点，
又∵MG⊥AB，∴MG∥BC，∴
同理可得，∴ME:MF=1:2． …………7分
(4) ME:MF=m ……………………8分
9.在△ABC中,AC=BC=2,∠C=90o，将一块等腰直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC，CB于D，E两点,如图1,2,3是旋转三角板得到的图形中的3 种情况，，研究：
⑴三角板绕点P旋转，观察线段PD和PE之间有什么数量关系？并结合图2加以证明。
⑵三角板绕点P旋转，△PBE是否能成为等腰三角形？若能，指出所有情况（即写出△PBE为等腰三角形时CE的长）；若不能，请说明理由。
⑶若将三角板的直角顶点放在斜边AB上的M处,且AM:MB=1:3，和前面一样操作,试问线段MD和ME之间有什么数量关系？并结合图4加以证明。
9、（1）PD=PE （提示：连结PC，证△PDC≌△PEB可得）
（2）能，CE的长： （3）MD：ME=1：3
10．图1是边长分别为4和3的两个等边三角形纸片ABC和C′D′E′叠放在一起（C与C′重合）。
（1）操作：固定△ABC，将△C′D′E′绕点C顺时针旋转30°得到△CDE，连结AD、BE，CE的延长线交AB于F（图2）；
探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论。
（2）操作：将图2中的△CDE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR（图3）；
请问：经过多少时间，△PQR与△ABC重叠部分的面积恰好等于 ？
（3）操作：图1中△C′D′E′固定，将△ABC移动，使顶点C落在C′E′的中点，边BC交D′E′于点M，边AC交D′C′于点N，设∠AC C′=α（30°＜α＜90，图4）；
探究：在图4中，线段CN·EM的值是否随α的变化而变化？如果没有变化，请你求出CN·EM的值，如果有变化，请你说明理由。
10.（1）BE=AD
证明：∵△ABC与△DCE是等边三角形 ∴∠ACB=∠DCE=60° CA=CB，CE=CD
∴∠BCE=∠ACD ∴△BCE≌△ACD ∴ BE=AD（也可用旋转方法证明BE=AD）
（2）设经过x秒重叠部分的面积是，如图在△CQT中
∵∠TCQ=30° ∠RQP=60°∴∠QTC=30° ∴∠QTC=∠TCQ
∴QT=QC=x∴ RT=3－x ∵∠RTS＋∠R=90° ∴∠RST=90°
由已知得×32 －（3－x）2=x＝1，x＝5，因为0≤x≤3，所以x=1
（3）C′N·E′M的值不变
证明：∵∠ACB=60°∴∠MCE′＋∠NCC′=120°
∵∠CNC′＋∠NCC′=120° ∴∠MCE′=∠CNC′
∵∠E′=∠C′ ∴△E′MC∽△C′CN
∴ ∴C′N·E′M=C′C·E′C=×=
11．请阅读下列材料：
已知：如图（1）在Rt△ABC中，∠BAC=90°，AB = AC，点D、E分别为线段BC上两动点，若∠DAE=45°.探究线段BD、DE、EC三条线段之间的数量关系.
小明的思路是：把△AEC绕点A顺时针旋转90°，得到△ABE′，连结E′D，
使问题得到解决.请你参考小明的思路探究并解决下列问题：
（1）猜想BD、DE、EC三条线段之间存在的数
量关系式，直接写出你的猜想； 图（1）
（2）当动点E在线段BC上，动点D运动在线
段CB延长线上时，如图（2），其它条件
不变，（1）中探究的结论是否发生改变？
请说明你的猜想并给予证明. 图（2）
（3）已知：如图(3)，等边三角形ABC中，点D、E在边AB上，且∠DCE=30°，请你找出一个条件，使线段DE、AD、EB能构成一个等腰三角形，并求出此时等腰三角形顶角的度数；
11.（1） DE2=BD2+EC2 ……1分
图（3）
（2）关系式DE2=BD2+EC2仍然成立 ………5分
证明：将△ADB沿直线AD对折，
得△AFD，连FE
∴ △AFD≌△ABD ……………6分
∴AF=AB，FD=DB
∠FAD=∠BAD，∠AFD=∠ABD
又∵AB=AC，∴AF=AC
∵∠FAE=∠FAD＋∠DAE=∠FAD＋45°
∠EAC=∠BAC－∠BAE=90°－(∠DAE－∠DAB)= 45°＋∠DAB
∴ ∠FAE=∠EAC 又∵ AE=AE ∴△AFE≌△ACE
∴ FE=EC , ∠AFE=∠ACE=45° ∠AFD=∠ABD=180°－∠ABC=135°
∴ ∠DFE=∠AFD－∠AFE=135°－45°=90°…………7分
∴在Rt△DFE中 DF2＋FE2=DE2 即DE2=BD2+EC2 ……8分
（2）当AD=BE时，线段DE、AD、EB能
构成一个等腰三角形.
如图②，与（1）类似，以CE为一边，作
∠ECF=∠ECB，在CF上截取CF=CB，可得
△CFE≌△CBE，△DCF≌△DCA.
∴AD=DF，EF=BE. 图②
∴∠DFE＝∠1＋∠2＝∠A＋∠B＝120°. ……………………………………5分
若使△DFE为等腰三角形，只需DF=EF，即AD=BE.
∴当AD=BE时，线段DE、AD、EB能构成一个等腰三角形. ……………6分
且顶角∠DFE为120°.
京模12.如图1，在△ACB和△AED中，AC=BC，AE=DE，∠ACB＝∠AED＝90°,点E在AB上， F是线段BD的中点，连结CE、FE.
（1）请你探究线段CE与FE之间的数量关系（直接写出结果，不需说明理由）；
（2）将图1中的△AED绕点A顺时针旋转，使△AED的一边AE恰好与△ACB的边AC在同一条直线上（如图2），连结BD，取BD的中点F，问（1）中的结论是否仍然成立，并说明理由；
（3）将图1中的△AED绕点A顺时针旋转任意的角度（如图3），连结BD，取BD的中点F，问（1）中的结论是否仍然成立，并说明理由．
12．（1）线段CE与FE之间的数量关系是CE=FE．………2分
（2）（1）中的结论仍然成立．
如图2，连结CF，延长EF交CB于点G．
∵ ∴ DE∥BC． ∴∠EDF=∠GBF．
又∵，DF=BF，∴ △EDF≌△GBF．
∴ EF=GF，BG＝DE＝AE． ∵ AC=BC， ∴ CE=CG．
∴∠EFC=90°，CF=EF． ∴ △CEF为等腰直角三角形．
∴∠CEF=45°．∴CE=FE ………5分
（3）（1）中的结论仍然成立．
如图3，取AD的中点M,连结EM，MF,取AB的中点N,连结FN，CN，CF．
∵DF=BF， ∴
∵AE=DE，∠AED=90°, ∴AM=EM，∠AME=90°.
∵CA=CB,∠ACB=90°,
∴，∠ANC=90°.
∴，FM=AN =CN.
∴四边形MFNA为平行四边形.
∴FN=AM=EM，∠AMF=∠FNA.
∴∠EMF=∠FNC. ∴△EMF≌△FNC.
∴FE = CF，∠EFM=∠FCN.
由，∠ANC=90°，可得∠CPF=90°.
∴∠FCN＋∠PFC=90°. ∴∠EFM＋∠PFC=90°.
∴∠EFC=90°. ∴ △CEF为等腰直角三角形．
∴∠CEF=45°. ∴ CE=FE．……………8分
另法:延长CF至G, 使FG=CF, 连结EG与DG. 证△DFG≌△FBC. 从而
DG=CB=AC, 再证△ACE≌△DEG
13.. 如图①，已知△ABC中，AB=AC，点P是BC上的一点，PN⊥AC于点N，PM⊥AB于点M，CG⊥AB于点G，则CG=PM+PN．
　　(1)如图②，若点Ｐ在ＢＣ的延长线上， 则ＰＭ、ＰＮ、ＣＧ三者是否还有上述关系，若有，请说明理由，若没有，猜想三者之间又有怎样的关系，并证明你的猜想；
　　(2)如图③，AC是正方形ABCD的对角线,AE=AB, 点P是BE上任一点, PN⊥AB于点N，PM⊥AC于点M，猜想ＰＭ、ＰＮ、ＡＣ有什么关系；（直接写出结论）
　　(3)观察图①、②、③的特性，请你根据这一特性构造一个图形，使它仍然具有ＰＭ、ＰＮ、ＣＧ这样的线段，并满足图①或图②的结论，写出相关题设的条件和结论.
　13．（1）猜想ＣＧ=ＰＭ－ＰＮ．
　　证明：过C点作CE⊥PM于E. 　∵PN⊥AB，CG⊥AB，∴四边形CGME是矩形.
　　∴ME=CG，CE∥AB． 　　∴∠B=∠ECP. 　　∵AB=AC，∴∠B=∠ACB=∠PCN.
　　∴∠ECP=∠PCN.　　∵∠PNC=∠PEC=90°，PC=PC，∴△PNC≌△PEC. ∴PN=PE .
　　∴CG= ME=PM－PE=PM－PN . ………4分
　　（2）PM+PN=AC . 　　证明：连接BD，交AC于O，过点P作PF⊥BD于F.
　　∵四边形ABCD是正方形，∴∠COB=90°，OB=OC=AC.
　　∵PM⊥AC，∴四边形PFOM为矩形.　∴MP=OF，PF∥AC.∴∠OEP=∠FPB.
　　∵AE=AB，∴∠OEP=∠ABP. 　　∴∠ABP=∠FPB.
　　∵PB=PB，∠PFB=∠PNB=90°，∴△PFB≌△BNP.
　　∴BF=PN.∴OB=OF+FB= PM+PN=AC. ………………8分
　　（3）点P是等腰三角形底边所在直线上的任意一点，点P到两腰的距离的和（或差）等于这个等腰三角形腰上的高.如图③，④都有BG=PM+PN.
　　如图⑤ＣＧ=ＰＭ－ＰＮ. ………………10分
G
E
A D
B C
图1
E
A G D F
B C
E
A D
B C
图2
图1
E
A G D F
B C
S
T
P
图1
A
B
C
D
E
P
图2
A
B
C
D
E
P
图3
A
B
C
D
E
M
图4
A
B
C
D
E
A
B
C
E
F
D
D
A
B
C
E
F
A
D
F
C
E
B
图9-1
图9-2
图9-3
P
C
D
A
B
图②
A
B
D
C
P
图①
A
B
C
D
E
R
P
H
Q
A
B
C
D
E
R
P
H
Q
A
B
C
D
E
R
P
H
Q
Q
H
P
R
E
D
C
B
A
Q
H
P
R
E
D
C
B
A
1
2
M
Q
H
P
R
E
D
C
B
A
E
图5
N
M
D
C
B
A
图4
F
N
M
E
D
C
B
A
N
M
E
D
C
B
A
图3
图2
H
K
F
C
B
E
N
D
A
M
图1
F
C
B
E
N
D
A
M
C
E
F
D
B
A
图1
F
C
E
D
B
A
图2
E
C
D
B
A
图3
FD
图2
图1