2010针对性训练-----综合压轴题
文档属性
| 名称 | 2010针对性训练-----综合压轴题 |
|
|
| 格式 | rar | ||
| 文件大小 | 327.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 新人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-06-02 00:00:00 | ||
图片预览





文档简介
针对性训练-----综合压轴题
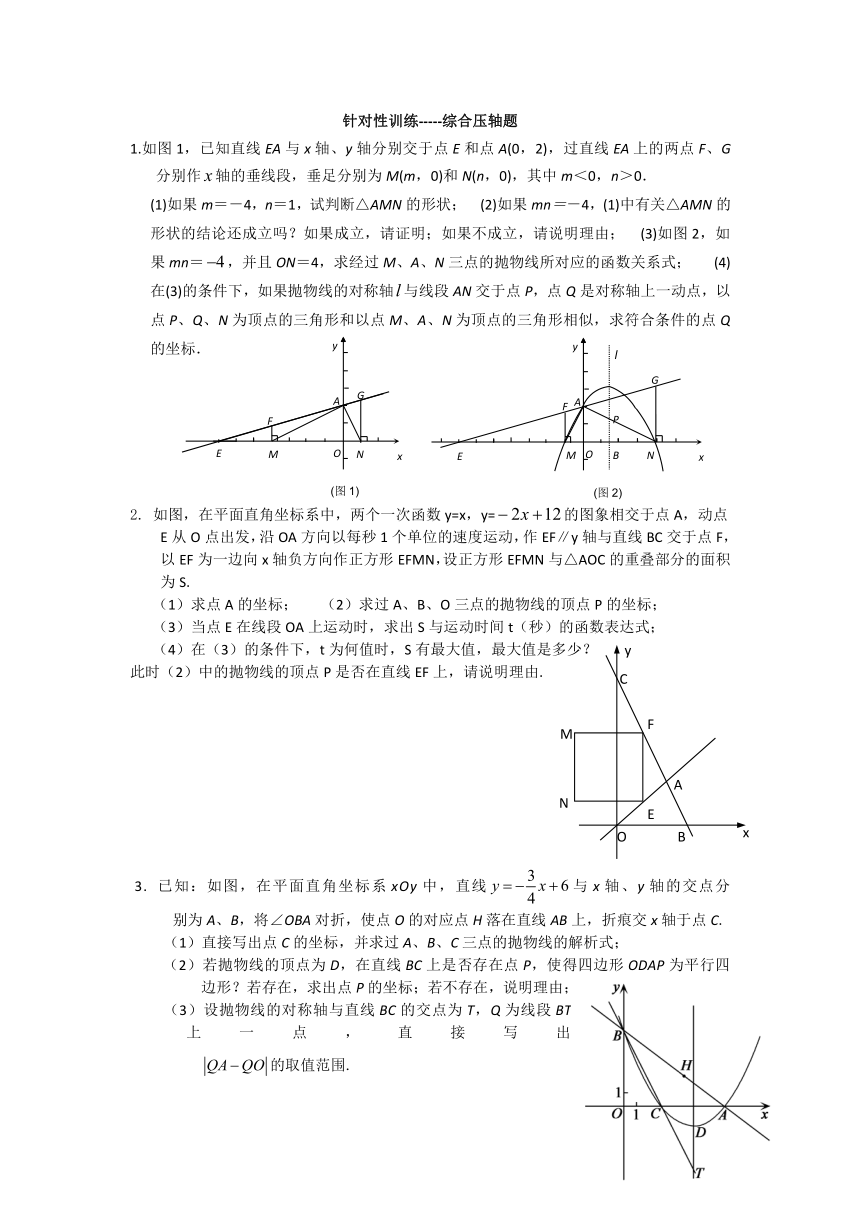
1.如图1,已知直线EA与x轴、y轴分别交于点E和点A(0,2),过直线EA上的两点F、G分别作轴的垂线段,垂足分别为M(m,0)和N(n,0),其中m<0,n>0.
(1)如果m=-4,n=1,试判断△AMN的形状; (2)如果mn=-4,(1)中有关△AMN的形状的结论还成立吗?如果成立,请证明;如果不成立,请说明理由; (3)如图2,如果mn=,并且ON=4,求经过M、A、N三点的抛物线所对应的函数关系式; (4)在(3)的条件下,如果抛物线的对称轴与线段AN交于点P,点Q是对称轴上一动点,以点P、Q、N为顶点的三角形和以点M、A、N为顶点的三角形相似,求符合条件的点Q的坐标.
2. 如图,在平面直角坐标系中,两个一次函数y=x,y=的图象相交于点A,动点E从O点出发,沿OA方向以每秒1个单位的速度运动,作EF∥y轴与直线BC交于点F,以EF为一边向x轴负方向作正方形EFMN,设正方形EFMN与△AOC的重叠部分的面积为S.
(1)求点A的坐标; (2)求过A、B、O三点的抛物线的顶点P的坐标;
(3)当点E在线段OA上运动时,求出S与运动时间t(秒)的函数表达式;
(4)在(3)的条件下,t为何值时,S有最大值,最大值是多少?
此时(2)中的抛物线的顶点P是否在直线EF上,请说明理由.
3. 已知:如图,在平面直角坐标系xOy中,直线与x轴、y轴的交点分
别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
(1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式;
(2)若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四
边形?若存在,求出点P的坐标;若不存在,说明理由;
(3)设抛物线的对称轴与直线BC的交点为T,Q为线段BT上一点,直接写出
的取值范围.
4.如图,现有两块全等的直角三角形纸板Ⅰ,Ⅱ,它们两直角边的长分别为1和2.将它们分别放置于平面直角坐标系中的,处,直角边在轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至处时,设与分别交于点,与轴分别交于点.
(1)求直线所对应的函数关系式;
(2)当点是线段(端点除外)上的动点时,试探究:
①点到轴的距离与线段的长是否总相等?请说明理由;
②两块纸板重叠部分(图中的阴影部分)的面积是否存在最大值?若存在,求出这个最大值及取最大值时点的坐标;若不存在,请说明理由.
5.在平面直角坐标系xOy中,抛物线 y=-x2+bx+c与x轴交于A、B 两点(点A在点B的左侧),与y轴交于点C,顶点为D,且点B的坐标为(1,0), 点C的坐标
为(0,3).
(1)求抛物线及直线AC的解析式;
(2)E、F是线段AC上的两点,且∠AEO=∠ABC,过点F作与y轴平行的直线交抛物线于点M,交x轴于点N.当MF=DE时,在x轴上是否存在点P,使得以点P、A、F、M为顶点的四边形是梯形? 若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q是位于抛物线对称轴左侧图象上的一点,试比较锐角∠QCO与∠BCO 的大小(直接写出结果,不要求写出求解过程,但要写出此时点 Q的横坐标x的取值范围).
6.如图,抛物线与x轴交于点A、B,与y轴交于点C,OA=4,AO=2OC,且抛物线对称轴为直线
(1)求该抛物线的函数表达式;
(2)已知矩形DEFG的一条边DE在线段AB上,顶点F、G分别在AC、BC上,设OD=m,矩形DEFG的面积为S,当矩形DEFG的面积S取得最大值时,连接DF并延长至点M,使,求出此时点M的坐标。
(3)若点Q是抛物线上一点,且横坐标为,点P是y轴上一点,是否存在这样的点P,使得是直角三角形,如果存在,求出点P的坐标,若不存在,请说明理由。
7.如图,对称轴为直线的抛物线经过点A(6,0)和B(0,4).
(1)求抛物线解析式及顶点坐标;
(2)设点E(,)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与之间的函数关系式,并写出自变量的取值范围;
①当平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形?
②是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
1.(1)△AMN是直角三角形.
依题意得OA=2,OM=4,ON=1,∴MN=OM+ON=4+1=5
在Rt△AOM中,AM===
在Rt△AON中,AN===
∴MN 2=AM 2+AN 2 ∴△AMN是直角三角形……2分
(2)答:(1)中的结论还成立.
依题意得OA=2,OM=-m,ON=n
∴MN=OM+ON=n-m
∴MN 2=(n-m) 2=n 2-2mn+m 2
∵mn=-4 ∴MN 2=n 2-2×(-4)+m 2=n 2+m 2+8
又∵在Rt△AOM中,AM===
在Rt△AON中,AN===
∴AM 2+AN 2=4+m 2+4+n 2=n 2+m 2+8
∴MN 2=AM 2+AN 2 ∴△AMN是直角三角形.…… 2分
(3) ∵mn=-4,n=4,∴.
设抛物线的函数关系式为y=a (x+1) (x-4).
∵抛物线经过点A(0,2) ∴-4a=2 解得a=-
∴所求抛物线的函数关系式为y=-(x+1) (x-4)即y=-x2+x+2 .
(4) 抛物线的对称轴与x轴的交点Q1符合条件,
∵l⊥MN,∠ANM=∠PN Q1,∴Rt△PN Q1∽Rt△ANM
∵抛物线的对称轴为x=,∴Q1(,0) ………………2分
∴NQ1=4-=.
过点N作NQ2⊥AN,交抛物线的对称轴于点Q2.
∴Rt△P Q2N、Rt△NQ2Q1、Rt△PNQ1和Rt△ANM两两相似
∴ 即Q1Q2=
∵点Q2位于第四象限,∴Q2(,)
因此,符合条件的点有两个,分别是Q1(,0),Q2(,).
2.(1)依题意得 解得 ∴点A的坐标为(4,4). …3分
(2)直线y=与x轴交点B的坐标为(6,0).
设过A、B、O的抛物线的表达式为y=ax2+bx,
依题意得解得
∴所求抛物线的表达式为.
=,∴点P坐标(3,). ………………7分
(3)设直线MF、NE与y轴交于点P、Q, 则△OQE是等腰直角三角形.
∵OE=1×t= t, ∴EQ=OQ=,∴E(,).
∵EF∥y轴, ∴PF=,=12-.
∴EF=PQ=12--=.
①当EF>QE时, 即>,解得.
∴当时,()=.
②当EF≤QE时,即≤,解得 .
∴当时,S=EF2=()2 . ………………………11分
(4)当时, =.
∴当时,S最大=12 .
当时,S最大=()2=9.
∴当时,S最大=12. ……………………………13分
当时,E(2,2),F(2,8),
∵P(3,),∴点P不在直线EF上. ……………………………14分
3. (1)点C的坐标为. - - - - - - - - - 1分
∵ 点A、B的坐标分别为,
∴ 可设过A、B、C三点的抛物线的解析式为.
将代入抛物线的解析式,得. - - - - - - - - - -2分
∴ 过A、B、C三点的抛物线的解析式为. - - - -3分
(2)可得抛物线的对称轴为,顶点D的坐标为
,设抛物线的对称轴与x轴的交点为G.
直线BC的解析式为.- - - - - 4分
设点P的坐标为.
解法一:如图8,作OP∥AD交直线BC于点P,
连结AP,作PM⊥x轴于点M.
∵ OP∥AD,
∴ ∠POM=∠GAD,tan∠POM=tan∠GAD.
∴ ,即.
解得. 经检验是原方程的解.
此时点P的坐标为. - - - - - - - -5分
但此时,OM<GA.
∵
∴ OP<AD,即四边形的对边OP与AD平行但不相等,
∴ 直线BC上不存在符合条件的点P. - - - - - - - - 6分
解法二:如图9,取OA的中点E,作点D关于点E的对称点P,作PN⊥x轴于点N. 则∠PEO=∠DEA,PE=DE.
可得△PEN≌△DEG .
由,可得E点的坐标为.
NE=EG=, ON=OE-NE=,NP=DG=.
∴ 点P的坐标为. - - - - - - - - - - - - 5分
∵ x=时,,
∴ 点P不在直线BC上.
∴ 直线BC上不存在符合条件的点P . - - - - - - - - 6分
(3)的取值范围是.- - - - - - - - - - - - 8分
说明:如图10,由对称性可知QO=QH,.当点Q与点B重合时,Q、H、A三点共线,取得最大值4(即为AH的长);设线段OA的垂直平分线与直线BC的交点为K,当点Q与点K重合时,取得最小值0.
4.(1)由直角三角形纸板的两直角边的长为1和2,知两点的坐标分别为.
设直线所对应的函数关系式为.
有解得
所以,直线所对应的函数关系式为.
(2)①点到轴距离与线段的长总相等.
因为点的坐标为,
所以,直线所对应的函数关系式为.
又因为点在直线上,
所以可设点的坐标为.
过点作轴的垂线,设垂足为点,则有.
因为点在直线上,所以有.
因为纸板为平行移动,故有,即.
又,所以.
法一:故,
从而有.
得,.
所以.
又有.
所以,得,而,
从而总有.
法二:故,可得.
故.
所以.
故点坐标为.
设直线所对应的函数关系式为,
有解得
所以,直线所对的函数关系式为.
将点的坐标代入,可得.解得.
而,从而总有.
②由①知,点的坐标为,点的坐标为.
.
当时,有最大值,最大值为.
取最大值时点的坐标为.
5.(1)抛物线 过B(1,0)、C(0,3)两点,
∴ 解得
∴ 抛物线的解析式为 y=-x 2-2x+3.………………1分
由y=-x 2-2x+3可得 A点坐标为(,0).
设直线AC的解析式为,
∴ 解得
∴ 直线AC的解析式为.……………………2分
(2)OA=OC=3,OB=1,
∴△AOC是等腰直角三角形,AC=,AB=4.
∴∠ECO=45°.
∠AEO=∠ABC,∠EAO=∠BAC,
∴△AEO∽△ABC. ∴. ∴. ∴AE=.
∴CE=AC-AE=-=.
过点E作EH⊥y轴于H. 可得EH=CH=1,OH=2.
∴E点的坐标为(-1, 2).
抛物线y=-x 2-2x+3顶点D的坐标为(-1,4),
∴ED=2.…………………3分 ∴MF=ED=2.
F在线段AC上,M在抛物线y=-x 2-2x+3上,
∴设F点的坐标为(x,x+3),M点的坐标为(x,-x2-2 x+3).
∴-x2-2 x+3-(x+3)=2.
解得x1= -2,x2= -1 (不合题意,舍去).
∴F点的坐标为(-2,1). ∴FN=NA=1.
在x轴上存在点P,使得以点P、A、F、M为顶点的四边形是梯形.
当FP∥MA时,可得. ∴. ∴.
∴P点的坐标为(-,0).……………4分
当MP∥FA时,可得. ∴PN=3. ∴P点的坐标为(-5,0).…5分
∴在x轴上存在点P使得以点P、A、F、M为顶点的四边形是梯形,点P的坐标为(-,0)或(-5,0).
(3) 当时,锐角;
当时,锐角;
当时,锐角.……………7分
6.
7.分析:(1)利用待定系数法可以求出抛物线解析式,(2)利用平行四边形OEAF的面积公式来建立函数关系式.①判断OEAF是否为菱形,关键是看能否由已知条件得到邻边相等,即需要将面积关系转化为线段关系,②假设存在符合条件的 E,考虑先满足条件“使得OEAF为正方形”,再看能否满足另外条件“在抛物线上”.
解:(1)由抛物线的对称轴是,可设解析式为.把A、B两点坐标代入上式,得故抛物线解析式为,顶点为
(2)因为点在抛物线上,位于第四象限,且坐标适合,
所以y<0,即 -y>0,-y表示点E到OA的距离.因为OA是的对角线,
所以.
因为抛物线与x轴焦点的横坐标分别为:x1=1,x2=6.又点E在第四象限,点E的纵坐标小于0,所以点E的横坐标1.的取值范围是1<<6.
1 根据题意,当S = 24时,即. 解得故所求的点E
有两个,分别为E1(3,-4),E2(4,-4).点E1(3,-4)满足OE = AE,所以是菱形;点E2(4,-4)不满足OE = AE,所以不是菱形.
1 当OA⊥EF,且OA = EF时,是正方形,此时点E的坐标只能是(3,-3).
而坐标为(3,-3)的点不在抛物线上,故不存在这样的点E,使为正方形.
特别提示:需要同时满足几个条件时,不妨先满足其中部分,再看是否满足其它条件.
l
(图2)
(图1)
N
M
E
F
P
G
B
A
x
O
y
y
N
M
F
E
O
G
x
A
-2
A
C
O
B
y
x
F
E
M
N
A
O
E
G
B
F
H
N
C
P
I
x
y
M
D
II
II
K
(第24题答图)
M
y
x
I
P
C
N
H
F
B
G
E
O
A
图9
图10
图8
1.如图1,已知直线EA与x轴、y轴分别交于点E和点A(0,2),过直线EA上的两点F、G分别作轴的垂线段,垂足分别为M(m,0)和N(n,0),其中m<0,n>0.
(1)如果m=-4,n=1,试判断△AMN的形状; (2)如果mn=-4,(1)中有关△AMN的形状的结论还成立吗?如果成立,请证明;如果不成立,请说明理由; (3)如图2,如果mn=,并且ON=4,求经过M、A、N三点的抛物线所对应的函数关系式; (4)在(3)的条件下,如果抛物线的对称轴与线段AN交于点P,点Q是对称轴上一动点,以点P、Q、N为顶点的三角形和以点M、A、N为顶点的三角形相似,求符合条件的点Q的坐标.
2. 如图,在平面直角坐标系中,两个一次函数y=x,y=的图象相交于点A,动点E从O点出发,沿OA方向以每秒1个单位的速度运动,作EF∥y轴与直线BC交于点F,以EF为一边向x轴负方向作正方形EFMN,设正方形EFMN与△AOC的重叠部分的面积为S.
(1)求点A的坐标; (2)求过A、B、O三点的抛物线的顶点P的坐标;
(3)当点E在线段OA上运动时,求出S与运动时间t(秒)的函数表达式;
(4)在(3)的条件下,t为何值时,S有最大值,最大值是多少?
此时(2)中的抛物线的顶点P是否在直线EF上,请说明理由.
3. 已知:如图,在平面直角坐标系xOy中,直线与x轴、y轴的交点分
别为A、B,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
(1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式;
(2)若抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四
边形?若存在,求出点P的坐标;若不存在,说明理由;
(3)设抛物线的对称轴与直线BC的交点为T,Q为线段BT上一点,直接写出
的取值范围.
4.如图,现有两块全等的直角三角形纸板Ⅰ,Ⅱ,它们两直角边的长分别为1和2.将它们分别放置于平面直角坐标系中的,处,直角边在轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至处时,设与分别交于点,与轴分别交于点.
(1)求直线所对应的函数关系式;
(2)当点是线段(端点除外)上的动点时,试探究:
①点到轴的距离与线段的长是否总相等?请说明理由;
②两块纸板重叠部分(图中的阴影部分)的面积是否存在最大值?若存在,求出这个最大值及取最大值时点的坐标;若不存在,请说明理由.
5.在平面直角坐标系xOy中,抛物线 y=-x2+bx+c与x轴交于A、B 两点(点A在点B的左侧),与y轴交于点C,顶点为D,且点B的坐标为(1,0), 点C的坐标
为(0,3).
(1)求抛物线及直线AC的解析式;
(2)E、F是线段AC上的两点,且∠AEO=∠ABC,过点F作与y轴平行的直线交抛物线于点M,交x轴于点N.当MF=DE时,在x轴上是否存在点P,使得以点P、A、F、M为顶点的四边形是梯形? 若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q是位于抛物线对称轴左侧图象上的一点,试比较锐角∠QCO与∠BCO 的大小(直接写出结果,不要求写出求解过程,但要写出此时点 Q的横坐标x的取值范围).
6.如图,抛物线与x轴交于点A、B,与y轴交于点C,OA=4,AO=2OC,且抛物线对称轴为直线
(1)求该抛物线的函数表达式;
(2)已知矩形DEFG的一条边DE在线段AB上,顶点F、G分别在AC、BC上,设OD=m,矩形DEFG的面积为S,当矩形DEFG的面积S取得最大值时,连接DF并延长至点M,使,求出此时点M的坐标。
(3)若点Q是抛物线上一点,且横坐标为,点P是y轴上一点,是否存在这样的点P,使得是直角三角形,如果存在,求出点P的坐标,若不存在,请说明理由。
7.如图,对称轴为直线的抛物线经过点A(6,0)和B(0,4).
(1)求抛物线解析式及顶点坐标;
(2)设点E(,)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与之间的函数关系式,并写出自变量的取值范围;
①当平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形?
②是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
1.(1)△AMN是直角三角形.
依题意得OA=2,OM=4,ON=1,∴MN=OM+ON=4+1=5
在Rt△AOM中,AM===
在Rt△AON中,AN===
∴MN 2=AM 2+AN 2 ∴△AMN是直角三角形……2分
(2)答:(1)中的结论还成立.
依题意得OA=2,OM=-m,ON=n
∴MN=OM+ON=n-m
∴MN 2=(n-m) 2=n 2-2mn+m 2
∵mn=-4 ∴MN 2=n 2-2×(-4)+m 2=n 2+m 2+8
又∵在Rt△AOM中,AM===
在Rt△AON中,AN===
∴AM 2+AN 2=4+m 2+4+n 2=n 2+m 2+8
∴MN 2=AM 2+AN 2 ∴△AMN是直角三角形.…… 2分
(3) ∵mn=-4,n=4,∴.
设抛物线的函数关系式为y=a (x+1) (x-4).
∵抛物线经过点A(0,2) ∴-4a=2 解得a=-
∴所求抛物线的函数关系式为y=-(x+1) (x-4)即y=-x2+x+2 .
(4) 抛物线的对称轴与x轴的交点Q1符合条件,
∵l⊥MN,∠ANM=∠PN Q1,∴Rt△PN Q1∽Rt△ANM
∵抛物线的对称轴为x=,∴Q1(,0) ………………2分
∴NQ1=4-=.
过点N作NQ2⊥AN,交抛物线的对称轴于点Q2.
∴Rt△P Q2N、Rt△NQ2Q1、Rt△PNQ1和Rt△ANM两两相似
∴ 即Q1Q2=
∵点Q2位于第四象限,∴Q2(,)
因此,符合条件的点有两个,分别是Q1(,0),Q2(,).
2.(1)依题意得 解得 ∴点A的坐标为(4,4). …3分
(2)直线y=与x轴交点B的坐标为(6,0).
设过A、B、O的抛物线的表达式为y=ax2+bx,
依题意得解得
∴所求抛物线的表达式为.
=,∴点P坐标(3,). ………………7分
(3)设直线MF、NE与y轴交于点P、Q, 则△OQE是等腰直角三角形.
∵OE=1×t= t, ∴EQ=OQ=,∴E(,).
∵EF∥y轴, ∴PF=,=12-.
∴EF=PQ=12--=.
①当EF>QE时, 即>,解得.
∴当时,()=.
②当EF≤QE时,即≤,解得 .
∴当时,S=EF2=()2 . ………………………11分
(4)当时, =.
∴当时,S最大=12 .
当时,S最大=()2=9.
∴当时,S最大=12. ……………………………13分
当时,E(2,2),F(2,8),
∵P(3,),∴点P不在直线EF上. ……………………………14分
3. (1)点C的坐标为. - - - - - - - - - 1分
∵ 点A、B的坐标分别为,
∴ 可设过A、B、C三点的抛物线的解析式为.
将代入抛物线的解析式,得. - - - - - - - - - -2分
∴ 过A、B、C三点的抛物线的解析式为. - - - -3分
(2)可得抛物线的对称轴为,顶点D的坐标为
,设抛物线的对称轴与x轴的交点为G.
直线BC的解析式为.- - - - - 4分
设点P的坐标为.
解法一:如图8,作OP∥AD交直线BC于点P,
连结AP,作PM⊥x轴于点M.
∵ OP∥AD,
∴ ∠POM=∠GAD,tan∠POM=tan∠GAD.
∴ ,即.
解得. 经检验是原方程的解.
此时点P的坐标为. - - - - - - - -5分
但此时,OM<GA.
∵
∴ OP<AD,即四边形的对边OP与AD平行但不相等,
∴ 直线BC上不存在符合条件的点P. - - - - - - - - 6分
解法二:如图9,取OA的中点E,作点D关于点E的对称点P,作PN⊥x轴于点N. 则∠PEO=∠DEA,PE=DE.
可得△PEN≌△DEG .
由,可得E点的坐标为.
NE=EG=, ON=OE-NE=,NP=DG=.
∴ 点P的坐标为. - - - - - - - - - - - - 5分
∵ x=时,,
∴ 点P不在直线BC上.
∴ 直线BC上不存在符合条件的点P . - - - - - - - - 6分
(3)的取值范围是.- - - - - - - - - - - - 8分
说明:如图10,由对称性可知QO=QH,.当点Q与点B重合时,Q、H、A三点共线,取得最大值4(即为AH的长);设线段OA的垂直平分线与直线BC的交点为K,当点Q与点K重合时,取得最小值0.
4.(1)由直角三角形纸板的两直角边的长为1和2,知两点的坐标分别为.
设直线所对应的函数关系式为.
有解得
所以,直线所对应的函数关系式为.
(2)①点到轴距离与线段的长总相等.
因为点的坐标为,
所以,直线所对应的函数关系式为.
又因为点在直线上,
所以可设点的坐标为.
过点作轴的垂线,设垂足为点,则有.
因为点在直线上,所以有.
因为纸板为平行移动,故有,即.
又,所以.
法一:故,
从而有.
得,.
所以.
又有.
所以,得,而,
从而总有.
法二:故,可得.
故.
所以.
故点坐标为.
设直线所对应的函数关系式为,
有解得
所以,直线所对的函数关系式为.
将点的坐标代入,可得.解得.
而,从而总有.
②由①知,点的坐标为,点的坐标为.
.
当时,有最大值,最大值为.
取最大值时点的坐标为.
5.(1)抛物线 过B(1,0)、C(0,3)两点,
∴ 解得
∴ 抛物线的解析式为 y=-x 2-2x+3.………………1分
由y=-x 2-2x+3可得 A点坐标为(,0).
设直线AC的解析式为,
∴ 解得
∴ 直线AC的解析式为.……………………2分
(2)OA=OC=3,OB=1,
∴△AOC是等腰直角三角形,AC=,AB=4.
∴∠ECO=45°.
∠AEO=∠ABC,∠EAO=∠BAC,
∴△AEO∽△ABC. ∴. ∴. ∴AE=.
∴CE=AC-AE=-=.
过点E作EH⊥y轴于H. 可得EH=CH=1,OH=2.
∴E点的坐标为(-1, 2).
抛物线y=-x 2-2x+3顶点D的坐标为(-1,4),
∴ED=2.…………………3分 ∴MF=ED=2.
F在线段AC上,M在抛物线y=-x 2-2x+3上,
∴设F点的坐标为(x,x+3),M点的坐标为(x,-x2-2 x+3).
∴-x2-2 x+3-(x+3)=2.
解得x1= -2,x2= -1 (不合题意,舍去).
∴F点的坐标为(-2,1). ∴FN=NA=1.
在x轴上存在点P,使得以点P、A、F、M为顶点的四边形是梯形.
当FP∥MA时,可得. ∴. ∴.
∴P点的坐标为(-,0).……………4分
当MP∥FA时,可得. ∴PN=3. ∴P点的坐标为(-5,0).…5分
∴在x轴上存在点P使得以点P、A、F、M为顶点的四边形是梯形,点P的坐标为(-,0)或(-5,0).
(3) 当时,锐角;
当时,锐角;
当时,锐角.……………7分
6.
7.分析:(1)利用待定系数法可以求出抛物线解析式,(2)利用平行四边形OEAF的面积公式来建立函数关系式.①判断OEAF是否为菱形,关键是看能否由已知条件得到邻边相等,即需要将面积关系转化为线段关系,②假设存在符合条件的 E,考虑先满足条件“使得OEAF为正方形”,再看能否满足另外条件“在抛物线上”.
解:(1)由抛物线的对称轴是,可设解析式为.把A、B两点坐标代入上式,得故抛物线解析式为,顶点为
(2)因为点在抛物线上,位于第四象限,且坐标适合,
所以y<0,即 -y>0,-y表示点E到OA的距离.因为OA是的对角线,
所以.
因为抛物线与x轴焦点的横坐标分别为:x1=1,x2=6.又点E在第四象限,点E的纵坐标小于0,所以点E的横坐标1
1 根据题意,当S = 24时,即. 解得故所求的点E
有两个,分别为E1(3,-4),E2(4,-4).点E1(3,-4)满足OE = AE,所以是菱形;点E2(4,-4)不满足OE = AE,所以不是菱形.
1 当OA⊥EF,且OA = EF时,是正方形,此时点E的坐标只能是(3,-3).
而坐标为(3,-3)的点不在抛物线上,故不存在这样的点E,使为正方形.
特别提示:需要同时满足几个条件时,不妨先满足其中部分,再看是否满足其它条件.
l
(图2)
(图1)
N
M
E
F
P
G
B
A
x
O
y
y
N
M
F
E
O
G
x
A
-2
A
C
O
B
y
x
F
E
M
N
A
O
E
G
B
F
H
N
C
P
I
x
y
M
D
II
II
K
(第24题答图)
M
y
x
I
P
C
N
H
F
B
G
E
O
A
图9
图10
图8
同课章节目录
