人教A版必修一第三章3.1.2用二分法求方程的近似解课件 (共24张PPT)
文档属性
| 名称 | 人教A版必修一第三章3.1.2用二分法求方程的近似解课件 (共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 838.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-24 10:01:58 | ||
图片预览







文档简介
课件24张PPT。3.1.2用二分法求方程的近似解复习思考:1.函数的零点2.零点存在的判定3.零点个数的求法 使f(x)=0的实数x叫做函数y=f(x)的零点 对于方程(1),可以利用一元二次方程的求根公式求解;
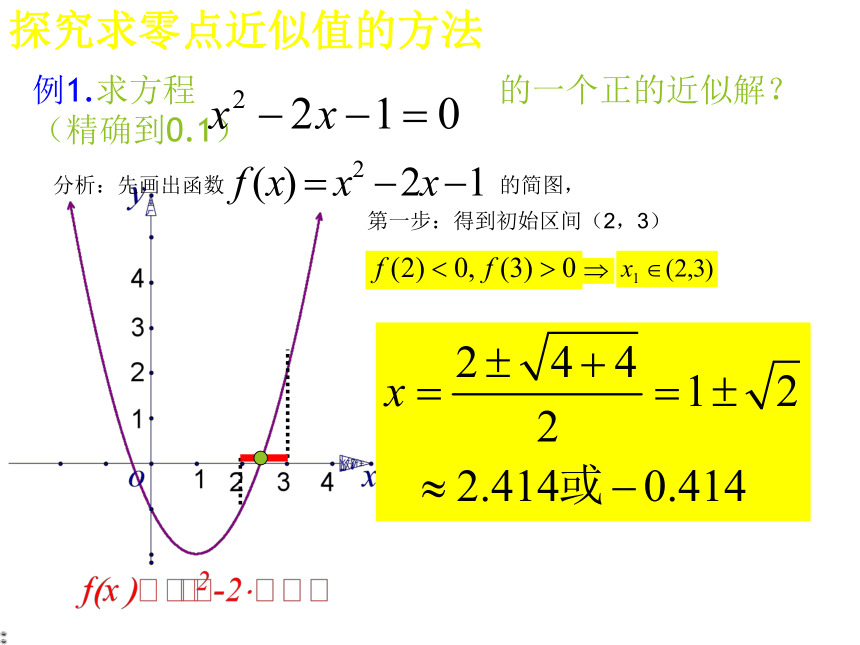
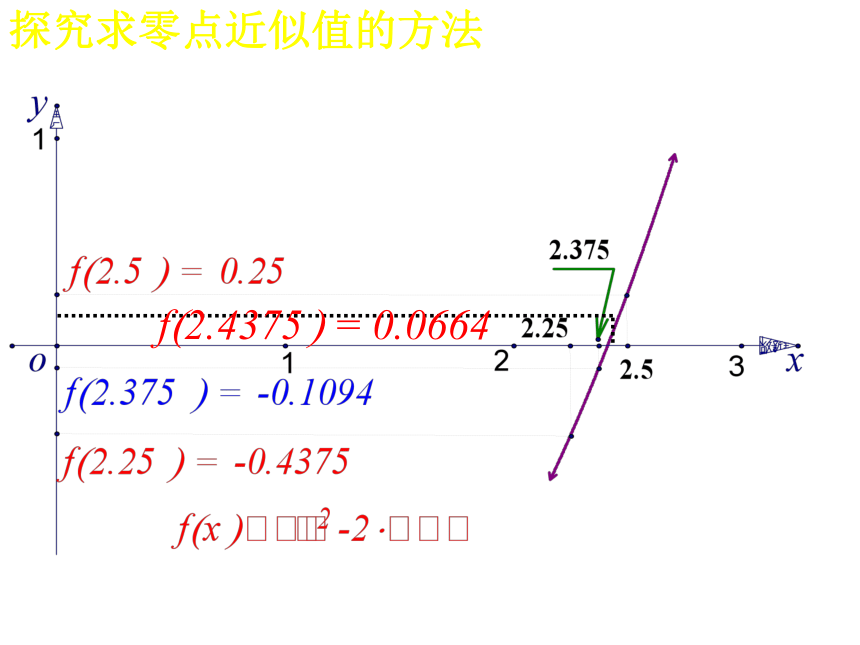
对于方程(2),可以通过画函数图象,判断与x轴的交点的横坐标求方程的近似解。 思考问题: 请同学们观察下面的两个方程,说一说你会用什么方法来求解方程. 例1.求方程 的一个正的近似解?(精确到0.1)分析:先画出函数 的简图,第一步:得到初始区间(2,3)探究求零点近似值的方法例1.求方程 的一个正的近似 解?(精确到0.1)分析:先画出函数 的简图,第一步:得到初始区间(2,3)第二步:取2与3的平均数2.5 探究求零点近似值的方法第三步:取2与2.5的平均数2.25 例1.求方程 的一个正的近似 解?(精确到0.1)分析:先画出函数 的简图,第一步:得到初始区间(2,3)第二步:取2与3的平均数2.5 第三步:取2与2.5的平均数2.25 探究求零点近似值的方法探究求零点近似值的方法例1.求方程 的一个正的近似 解?(精确到0.1)分析:先画出函数 的简图,第一步:得到初始区间(2,3)第二步:取2与3的平均数2.5 第三步:取2与2.5的平均数2.25 如此继续取下去得: 探究求零点近似值的方法探究求零点近似值的方法例1.求方程 的一个正的近似 解?(精确到0.1)分析:先画出函数 的简图,第一步:得到初始区间(2,3)第二步:取2与3的平均数2.5 第三步:取2与2.5的平均数2.25 第四步:因为2.375与2.4375精确到0.1的近似值都为2.4,所以此方程的近似解为 x1≈2.4.2.4375 -2.375=0.0625 <0.1探究过程总结先画出函数 的简图,第一步:得到初始区间(2,3)第二步:取2与3的平均数2.5 第三步:取2与2.5的平均数2.25 最后一步:因为2.375与2.4375精确到0.1的近似值都为2.4,所以此方程的近似解为 x1≈2.4.2.4375 -2.375=0.0625 <0.1以上这种求零点近似值的方法叫做二分法二分法的概念1.二分法的描述:
对于区间[a,b]上连续不断、且f(a)f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法。概念提升 对于在区间 上连续不断且 的函
数 ,通过不断地把函数 的零点所在的区
间一分为二,使区间的两个端点逐步逼近零点,进而得到
零点近似值的方法叫做二分法(bisection).1.二分法概念2.用二分法求一元方程f(x)=0的近似解的基本步骤: 第一步 确定初始区间[a,b],验证f(a)f(b)<0第二步 求区间[a,b]两端点的平均值第三步 计算f(c) 并判断:(1)如果f(c)=0,则c就是f(x)的零点,计算终止; (2)如果f(a)f(c)<0,则零点 ,否则零点
。 第四步 重复步骤2~3,直至所得区间的两端点差的绝对值小于要求的精确值,则零点的近似值为所得区间内的任一数。一般取其中点为近似值。二分法的基本步骤周而复始怎么办? 精确度上来判断.定区间,找中点, 中值计算两边看.同号去,异号算, 零点落在异号间.口 诀所以x=2.53125为函数f(x)=lnx+2x-6在区间(2,3)内的零点近似值,也即方程lnx=-2x+6的近似解x1≈2.53。例2:求方程lnx=-2x+6的近似解(精确度为0.0 1)。解:分别画出函数y=lnx和y=-2x+6的图象,这两个图象交点的横坐标就是方程lnx=-2x+6 的解,由图象可以发现,方程有惟一解,记为x1,并且这个解在区间(2,3)内。设函数f(x)=lnx+2x-6,用计算器计算得:f(2.5)<0, f(3)>0 x1∈(2.5,3)
f(2.5)<0, f(2.5625)>0 x1∈(2.5,2.5625)
f(2.53125)<0, f(2.5625)>0 x1∈(2.53125,2.5625)f(2.53125)<0, f(2.546875)>0 x1∈(2.53125,2.546875) f(2.5)<0, f(2.625)>0 x1∈(2.5,2.625) f(2)<0, f(3)>0 x1∈(2,3)
f(2.5)<0, f(2.75)>0 x1∈(2.5,2.75) f(2.53125)<0, f(2.5390625)>0 x1∈(2.53125,2.5390625)练习练习小结 转化思想逼近思想数学
源于生活数学
用于生活小结二分法数形结合1.寻找解所在的区间2.不断二分解所在的区间3.根据精确度得出近似解用二分法求
方程的近似解算法思想应用生活中也常常会用到二分法思想: 例3 在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路发生了故障。这是一条10km长的线路,如何迅速查出故障所在?
???????如果沿着线路一小段一小段查找,困难很多。每查一个点要爬一次电线杆子,10km长,大约有200多根电线杆子呢。
???????想一想,维修线路的工人师傅至少经过几次查找使故障范围缩小到50~100m左右?应用探究求零点近似值的方法例4. 从上海到旧金山的海底电缆有15个接点,现在某接点发生故障,需及时修理,为了尽快断定故障发生点,一般至多需要检查接点的个数为几个?答:至多检查3个接点.应用练习1.用二分法求函数的零点,函数的零点总位于区间[an,bn]上,当 时函数的近似零点与真正零点的误差不超过( )
A.m B.m/2 C. 2m D. m/4B取中点为近似零点真正的零点应用练习2. 在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路发生了故障,这一条10km长的线路,如何迅速查出故障所在? 要把故障可能发生的范围缩小到50~100m左右,即一两根电线杆附近,要检查多少次?算一算:答:7次答:用二分法第2次:10000÷22=2500第1次:10000÷2=5000第3次:10000÷23=1250第4次:10000÷24=625第5次:10000÷25=312.5第6次:10000÷26=156.25第7次:10000÷27=78.125小结二分法是求函数零点近似解的一种计算方法.
用二分法求函数零点的一般步骤:
(1)零点存在性定理,求出初始区间;
(2)进行计算,确定下一区间
(3)循环进行,达到精确要求⒊二分法渗透了极限和算法的思想.
对于方程(2),可以通过画函数图象,判断与x轴的交点的横坐标求方程的近似解。 思考问题: 请同学们观察下面的两个方程,说一说你会用什么方法来求解方程. 例1.求方程 的一个正的近似解?(精确到0.1)分析:先画出函数 的简图,第一步:得到初始区间(2,3)探究求零点近似值的方法例1.求方程 的一个正的近似 解?(精确到0.1)分析:先画出函数 的简图,第一步:得到初始区间(2,3)第二步:取2与3的平均数2.5 探究求零点近似值的方法第三步:取2与2.5的平均数2.25 例1.求方程 的一个正的近似 解?(精确到0.1)分析:先画出函数 的简图,第一步:得到初始区间(2,3)第二步:取2与3的平均数2.5 第三步:取2与2.5的平均数2.25 探究求零点近似值的方法探究求零点近似值的方法例1.求方程 的一个正的近似 解?(精确到0.1)分析:先画出函数 的简图,第一步:得到初始区间(2,3)第二步:取2与3的平均数2.5 第三步:取2与2.5的平均数2.25 如此继续取下去得: 探究求零点近似值的方法探究求零点近似值的方法例1.求方程 的一个正的近似 解?(精确到0.1)分析:先画出函数 的简图,第一步:得到初始区间(2,3)第二步:取2与3的平均数2.5 第三步:取2与2.5的平均数2.25 第四步:因为2.375与2.4375精确到0.1的近似值都为2.4,所以此方程的近似解为 x1≈2.4.2.4375 -2.375=0.0625 <0.1探究过程总结先画出函数 的简图,第一步:得到初始区间(2,3)第二步:取2与3的平均数2.5 第三步:取2与2.5的平均数2.25 最后一步:因为2.375与2.4375精确到0.1的近似值都为2.4,所以此方程的近似解为 x1≈2.4.2.4375 -2.375=0.0625 <0.1以上这种求零点近似值的方法叫做二分法二分法的概念1.二分法的描述:
对于区间[a,b]上连续不断、且f(a)f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法。概念提升 对于在区间 上连续不断且 的函
数 ,通过不断地把函数 的零点所在的区
间一分为二,使区间的两个端点逐步逼近零点,进而得到
零点近似值的方法叫做二分法(bisection).1.二分法概念2.用二分法求一元方程f(x)=0的近似解的基本步骤: 第一步 确定初始区间[a,b],验证f(a)f(b)<0第二步 求区间[a,b]两端点的平均值第三步 计算f(c) 并判断:(1)如果f(c)=0,则c就是f(x)的零点,计算终止; (2)如果f(a)f(c)<0,则零点 ,否则零点
。 第四步 重复步骤2~3,直至所得区间的两端点差的绝对值小于要求的精确值,则零点的近似值为所得区间内的任一数。一般取其中点为近似值。二分法的基本步骤周而复始怎么办? 精确度上来判断.定区间,找中点, 中值计算两边看.同号去,异号算, 零点落在异号间.口 诀所以x=2.53125为函数f(x)=lnx+2x-6在区间(2,3)内的零点近似值,也即方程lnx=-2x+6的近似解x1≈2.53。例2:求方程lnx=-2x+6的近似解(精确度为0.0 1)。解:分别画出函数y=lnx和y=-2x+6的图象,这两个图象交点的横坐标就是方程lnx=-2x+6 的解,由图象可以发现,方程有惟一解,记为x1,并且这个解在区间(2,3)内。设函数f(x)=lnx+2x-6,用计算器计算得:f(2.5)<0, f(3)>0 x1∈(2.5,3)
f(2.5)<0, f(2.5625)>0 x1∈(2.5,2.5625)
f(2.53125)<0, f(2.5625)>0 x1∈(2.53125,2.5625)f(2.53125)<0, f(2.546875)>0 x1∈(2.53125,2.546875) f(2.5)<0, f(2.625)>0 x1∈(2.5,2.625) f(2)<0, f(3)>0 x1∈(2,3)
f(2.5)<0, f(2.75)>0 x1∈(2.5,2.75) f(2.53125)<0, f(2.5390625)>0 x1∈(2.53125,2.5390625)练习练习小结 转化思想逼近思想数学
源于生活数学
用于生活小结二分法数形结合1.寻找解所在的区间2.不断二分解所在的区间3.根据精确度得出近似解用二分法求
方程的近似解算法思想应用生活中也常常会用到二分法思想: 例3 在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路发生了故障。这是一条10km长的线路,如何迅速查出故障所在?
???????如果沿着线路一小段一小段查找,困难很多。每查一个点要爬一次电线杆子,10km长,大约有200多根电线杆子呢。
???????想一想,维修线路的工人师傅至少经过几次查找使故障范围缩小到50~100m左右?应用探究求零点近似值的方法例4. 从上海到旧金山的海底电缆有15个接点,现在某接点发生故障,需及时修理,为了尽快断定故障发生点,一般至多需要检查接点的个数为几个?答:至多检查3个接点.应用练习1.用二分法求函数的零点,函数的零点总位于区间[an,bn]上,当 时函数的近似零点与真正零点的误差不超过( )
A.m B.m/2 C. 2m D. m/4B取中点为近似零点真正的零点应用练习2. 在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路发生了故障,这一条10km长的线路,如何迅速查出故障所在? 要把故障可能发生的范围缩小到50~100m左右,即一两根电线杆附近,要检查多少次?算一算:答:7次答:用二分法第2次:10000÷22=2500第1次:10000÷2=5000第3次:10000÷23=1250第4次:10000÷24=625第5次:10000÷25=312.5第6次:10000÷26=156.25第7次:10000÷27=78.125小结二分法是求函数零点近似解的一种计算方法.
用二分法求函数零点的一般步骤:
(1)零点存在性定理,求出初始区间;
(2)进行计算,确定下一区间
(3)循环进行,达到精确要求⒊二分法渗透了极限和算法的思想.
