人教A版第三章3.1.1方程的根与函数的零点课件(共23张ppt)
文档属性
| 名称 | 人教A版第三章3.1.1方程的根与函数的零点课件(共23张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 717.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-24 10:25:08 | ||
图片预览






文档简介
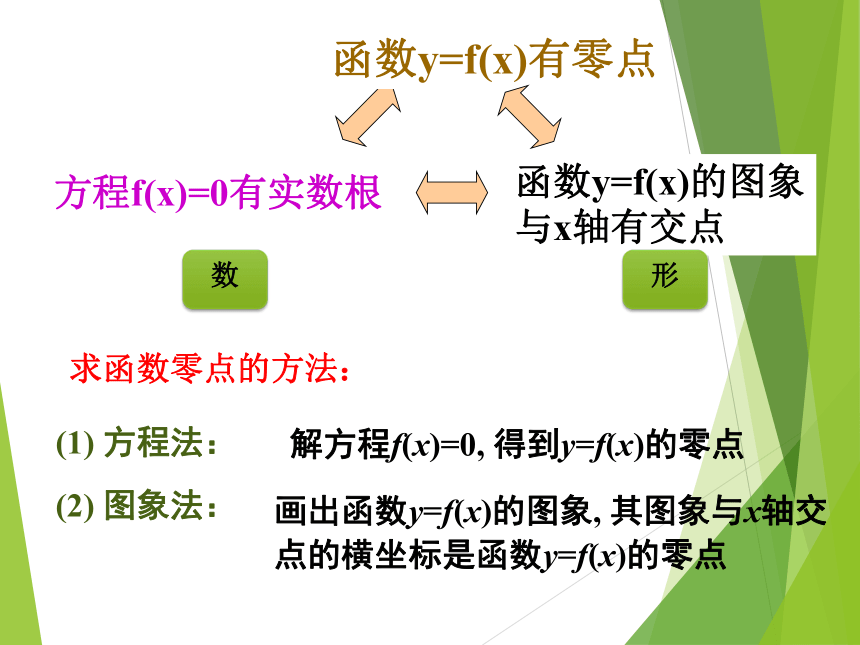
课件23张PPT。3.1.1方程的根与函数的零点先来观察几个具体的一元二次方程的根及其相应的二次函数的图象:无实根无交点一、复习引入一般一元二次方程与相应二次函数的关系x1,x2(x1,0),(x2,0)x1=x2(x1,0)无实根无交点 对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点。函数零点的定义:注意:零点指的是一个实数;不是一个点。二、新课讲解求函数零点的方法:(1) 方程法:(2) 图象法:解方程f(x)=0, 得到y=f(x)的零点画出函数y=f(x)的图象, 其图象与x轴交点的横坐标是函数y=f(x)的零点方程f(x)=0有实数根函数y=f(x)的图象
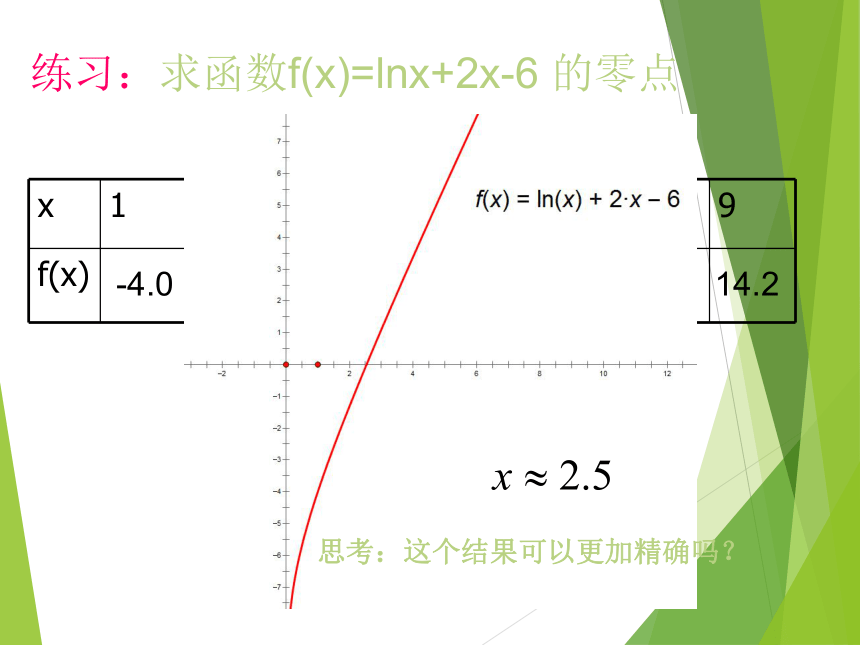
与x轴有交点函数y=f(x)有零点数形Q1: 求函数 的零点 Q4:求函数 的零点Q2: 求函数 的零点Q3: 求函数 的零点练习:求函数f(x)=lnx+2x-6 的零点-4.0-1.31.13.45.67.89.912.114.2思考:这个结果可以更加精确吗?1.当A,B与x轴是怎样的位置关系时,AB间一段
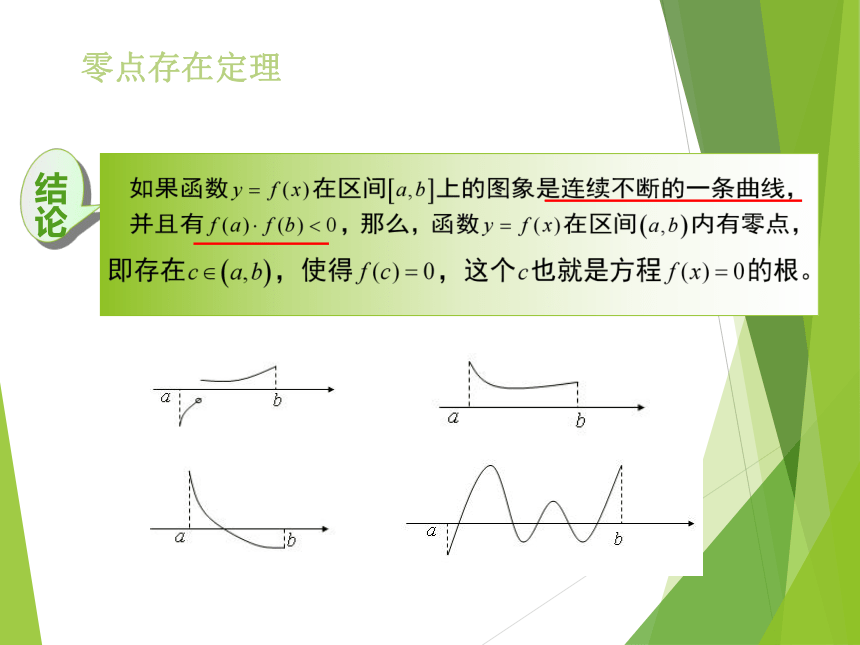
连续不断的函数图像与x轴一定有交点?2.A,B与x轴的位置关系如何用数学符号(式子)表示?零点存在定理思考4:若函数具备了(1)中的条件,加上什么条件,函数y=f(x)在区间(a,b)上可存在唯一零点?思考3:若在区间[a,b]上连续函数f(x)满足f(a)f(b)<0,是否意味着函数f(x)在[a,b]上恰有
一个零点? 思考2::若连续函数f(x)在[a,b]上有一个零点,是否一定有f(a)f(b)<0? 思考1:函数具备了哪些条件,就可确定它有
零点存在呢?例1:求函数f(x)=lnx+2x-6 的零点的个数-4.0-1.31.13.45.67.89.912.114.2
2. 函数 f(x) =2x +3x 的零点所在的一个区间是()A.(-2,-1)
C.(0,1)B.(-1,0)
D.(1,2)答案:B
3.(2011 年广东汕头测试)根据表格中的数据,可以判定函数
f(x)=ex-x-2 的一个零点所在的区间为(k,k+1)(k∈Z),则 k的值为()CA.-1B.0C.1D.2解析:由表,可知:当 k=1 时,f(1)·f(2)<0,∴零点在(1,2)内.B四、课堂小结1.函数零点的概念. 3.函数零点存在的条件.4.数学思想. 2. 三者间的关系。作业:P92 A组 2,1.若函数 f(x)=ax+b有一个零点2,求函数
g(x)=bx2-ax的零点。4. 函数 有几个零点?谢谢!1.函数f(x)=x(x2-16)的零点为(? )
A. (0,0),(4,0)?? ?? ? B.0,4????
C. (–4,0),(0,0),(4,0)???? D.–4,0,4三、课堂练习DCB5. 已知关于x的方程 的一个根在(-2,0)内,另一根在(1,3)内,求实数a的取值范围. 4. 关于x的方程 的根在(-2,0)内,求实数a的取值范围.
与x轴有交点函数y=f(x)有零点数形Q1: 求函数 的零点 Q4:求函数 的零点Q2: 求函数 的零点Q3: 求函数 的零点练习:求函数f(x)=lnx+2x-6 的零点-4.0-1.31.13.45.67.89.912.114.2思考:这个结果可以更加精确吗?1.当A,B与x轴是怎样的位置关系时,AB间一段
连续不断的函数图像与x轴一定有交点?2.A,B与x轴的位置关系如何用数学符号(式子)表示?零点存在定理思考4:若函数具备了(1)中的条件,加上什么条件,函数y=f(x)在区间(a,b)上可存在唯一零点?思考3:若在区间[a,b]上连续函数f(x)满足f(a)f(b)<0,是否意味着函数f(x)在[a,b]上恰有
一个零点? 思考2::若连续函数f(x)在[a,b]上有一个零点,是否一定有f(a)f(b)<0? 思考1:函数具备了哪些条件,就可确定它有
零点存在呢?例1:求函数f(x)=lnx+2x-6 的零点的个数-4.0-1.31.13.45.67.89.912.114.2
2. 函数 f(x) =2x +3x 的零点所在的一个区间是()A.(-2,-1)
C.(0,1)B.(-1,0)
D.(1,2)答案:B
3.(2011 年广东汕头测试)根据表格中的数据,可以判定函数
f(x)=ex-x-2 的一个零点所在的区间为(k,k+1)(k∈Z),则 k的值为()CA.-1B.0C.1D.2解析:由表,可知:当 k=1 时,f(1)·f(2)<0,∴零点在(1,2)内.B四、课堂小结1.函数零点的概念. 3.函数零点存在的条件.4.数学思想. 2. 三者间的关系。作业:P92 A组 2,1.若函数 f(x)=ax+b有一个零点2,求函数
g(x)=bx2-ax的零点。4. 函数 有几个零点?谢谢!1.函数f(x)=x(x2-16)的零点为(? )
A. (0,0),(4,0)?? ?? ? B.0,4????
C. (–4,0),(0,0),(4,0)???? D.–4,0,4三、课堂练习DCB5. 已知关于x的方程 的一个根在(-2,0)内,另一根在(1,3)内,求实数a的取值范围. 4. 关于x的方程 的根在(-2,0)内,求实数a的取值范围.
