用正多边形拼地板
图片预览









文档简介
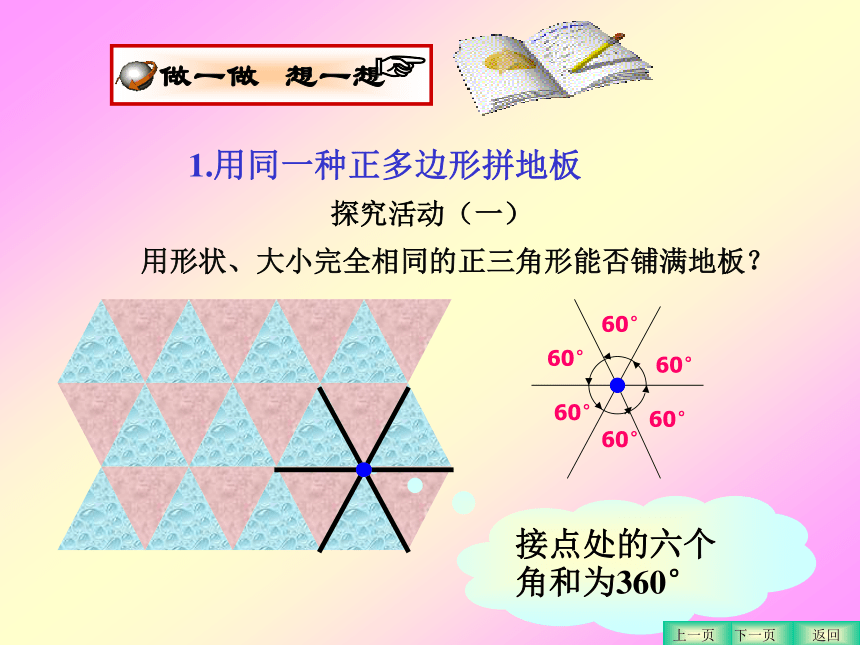
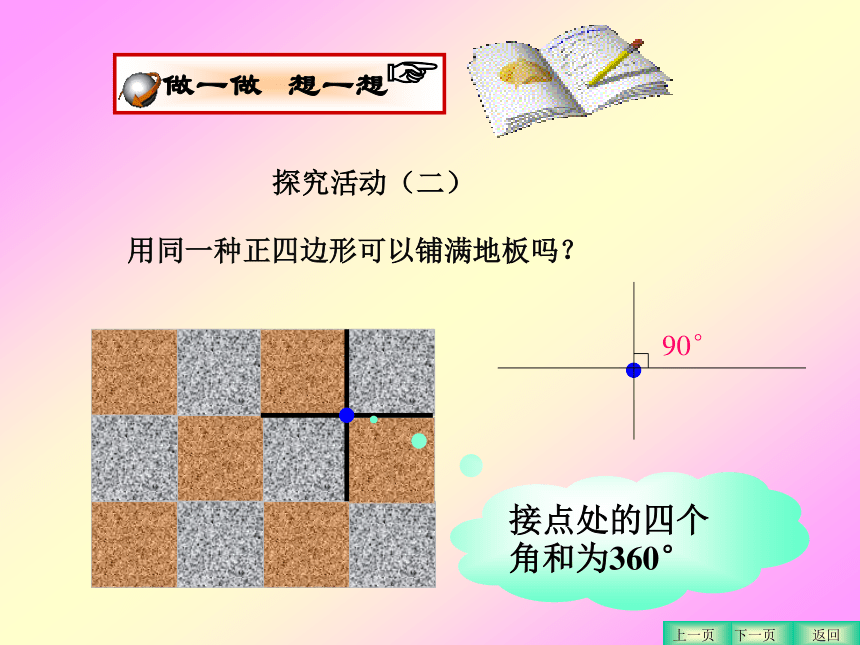
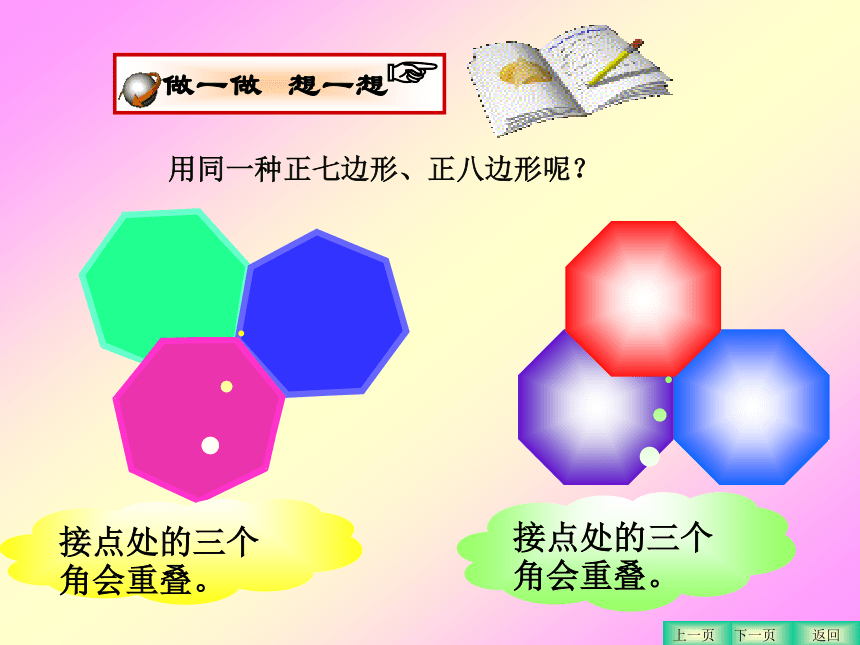
课件51张PPT。§9.3 用正多边形拼地板华师大版七年级下册第九章第三节图片欣赏提出问题课堂小结探究发现总结交流拓展探究图案欣赏随堂练习图例欣赏 欣赏左边地板图案时,你是否想到这些图案中所蕴含的数学道理呢? 返回下一页上一页在下列的图案中,你看到了哪些图形?返回下一页上一页 还有哪些正多边形可用来拼地板? 返回下一页上一页用正多边形拼地板探究问题究竟用什么样的正多边形能拼成一个既不留下一丝空白,又不相互重叠的平面图形呢?活动准备① n边形的内角和公式:② 正多边形每个内角=(n-2) ×180°探究活动(一)用形状、大小完全相同的正三角形能否铺满地板?接点处的六个角和为360°60°60°60°60°60°60°返回下一页上一页1.用同一种正多边形拼地板 探究活动(二)用同一种正四边形可以铺满地板吗?接点处的四个角和为360°返回下一页上一页议一议:探究活动(三) 2.正六边形能铺满地板吗?说说理由。 1.正五边形能铺满地板吗?说说理由。 3.还能找到能铺满地板的其他图形吗?返回下一页上一页正五边形可以铺满地板吗?接点处的四个角会重叠。正六边形可以铺满地板吗?120 °120 °120 °接点处的三个角和为360°返回下一页上一页用同一种正七边形、正八边形呢?接点处的三个角会重叠。接点处的三个角会重叠。返回下一页上一页我们发现:
(1)能用来拼地板的正多边形有:_________________________________正三角形、正方形、正六边形正五边形、正七边形、······正多边形能否拼成地板与什么有关呢?请把你的想法说出来结论:(2)不能用来拼地板的正多边形有:
_____________________________________________返回下一页上一页正八边形、计算正多边形内角并判断能否拼地板144o150o×××××60o90o108o120o135o√√√×××140o返回下一页上一页在交流中达成共识 概括: 要用正多边形铺满地板的关键是看:这种正多边形的一个内角的倍数是否是360°,在正多边形里,正三角形的每个内角都是60°,正四边形的每个内角都是90°,正六边形的每个内角都是120°,这三种多边形的一个内角的倍数都是360°,而其他的正多边形的每个内角的倍数都不是360°,所以说:在正多边形里只有正三角形、正四边形、正六边形可以铺满地板,而其他的正多边形不可铺铺满地板。 返回下一页上一页结论:使用某种给定的三角形可以铺满地板吗?四边形呢?任意的三角形和四边形都能铺满地板。试一试:探究活动(四)
----创意空间 用同一种平面图形如果不能铺满地板,用两种或者两种以上平面图形能不能铺满地板呢?返回下一页上一页2.多种正多边形拼地板问题拓展探究: 实际上,美观的图案是需要多种图形的,下面请同学们看一看哪几种正多边形可拼成地板?拼成什么样的图案?返回下一页上一页拓展探究:多种正多边形拼地板问题 实际上,美观的图案是需要多种图形的,下面请同学们看一看哪几种正多边形可拼成地板?拼成什么样的图案?返回下一页上一页拓展探究:多种正多边形拼地板问题 实际上,美观的图案是需要多种图形的,下面请同学们看一看哪几种正多边形可拼成地板?拼成什么样的图案?返回下一页上一页 与同学讨论,得出多种多边形拼成地板要满足的条件: 返回下一页上一页 围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就拼成一个平面图形。就说它们能拼地板。在交流中达成共识 概括:结论:返回下一页上一页(1)正三角形与正方形注意:同一个组合会有不同的密铺结果图例:返回下一页上一页(2)正三角形与正六边形注意:同一个组合会有不同的密铺结果图例:返回下一页上一页(3)正方形与正八边形图例:思考:还有其它的组合吗?返回下一页上一页正五边形、正十边形围绕一点能拼成360o,但能扩展到整个平面,即铺满地面吗?尽管能围绕一点拼成360o,但不能扩展到整个平面。(4)三种正多边形的平面密铺正十二边形与正方形、正六边形的平面密铺正六边形与正方形、正三角形的平面密铺
图例:返回下一页上一页1.商店出售下列形状的地砖:⑴正三角形⑵正方形⑶正五边形
(4)正六边形,若只选购其中某一种地砖铺满地面,可供选
择的地砖共有( )
A.1种 B. 2种 C. 3种 D. 4种
2.能够铺满地面的边长都相等的正多边形的组合是( )
A.正三角形和正方形 B. 正方形和正六边形
C.正三角形和正十二边形 D. 正三角形、正方形和正六边形
3.下列图形组合中,能够铺满地面的是( )
A.任意一种三角形和任意一种四边形
C.任意一种三角形和任意一种梯形 D.正八边形和等腰直角三角形
练习:CACDC返回下一页上一页选择题(可能有多个答案)B.正五边形和正十边形用正五边形和什么多边形能铺满地板?延伸探究:返回下一页上一页 1.平面图形的密铺指没有空隙和不重叠的拼接; 2.用一种或多种正多边形铺满地面的关键是:围绕一点拼在一起的几个内角加在一起恰好组成一个周角,这是多边形铺满地面的必须条件。3.有那些图形能组成平面密铺本节课你有什么收获?小结:发现二:
发现一:
同一种多边形进行平面密铺的图形只有三种:三角形、四边形、正六边形多种多边形能进行平面密铺的条件是:(1)拼接在同一点的各个角的度数和是360度(2)相邻的多边形有公共边返回下一页上一页(正五边形和正十边形是例外)图案欣赏3.有那些图形能组成平面密铺返回图案欣赏:返回下一页上一页密铺在现实生活中应用非常广泛.图案欣赏:图案欣赏: 图案欣赏:图案欣赏:图案欣赏:图案欣赏:图案欣赏:图案欣赏:图案欣赏:祝同学们
学习进步再见返回?
(1)能用来拼地板的正多边形有:_________________________________正三角形、正方形、正六边形正五边形、正七边形、······正多边形能否拼成地板与什么有关呢?请把你的想法说出来结论:(2)不能用来拼地板的正多边形有:
_____________________________________________返回下一页上一页正八边形、计算正多边形内角并判断能否拼地板144o150o×××××60o90o108o120o135o√√√×××140o返回下一页上一页在交流中达成共识 概括: 要用正多边形铺满地板的关键是看:这种正多边形的一个内角的倍数是否是360°,在正多边形里,正三角形的每个内角都是60°,正四边形的每个内角都是90°,正六边形的每个内角都是120°,这三种多边形的一个内角的倍数都是360°,而其他的正多边形的每个内角的倍数都不是360°,所以说:在正多边形里只有正三角形、正四边形、正六边形可以铺满地板,而其他的正多边形不可铺铺满地板。 返回下一页上一页结论:使用某种给定的三角形可以铺满地板吗?四边形呢?任意的三角形和四边形都能铺满地板。试一试:探究活动(四)
----创意空间 用同一种平面图形如果不能铺满地板,用两种或者两种以上平面图形能不能铺满地板呢?返回下一页上一页2.多种正多边形拼地板问题拓展探究: 实际上,美观的图案是需要多种图形的,下面请同学们看一看哪几种正多边形可拼成地板?拼成什么样的图案?返回下一页上一页拓展探究:多种正多边形拼地板问题 实际上,美观的图案是需要多种图形的,下面请同学们看一看哪几种正多边形可拼成地板?拼成什么样的图案?返回下一页上一页拓展探究:多种正多边形拼地板问题 实际上,美观的图案是需要多种图形的,下面请同学们看一看哪几种正多边形可拼成地板?拼成什么样的图案?返回下一页上一页 与同学讨论,得出多种多边形拼成地板要满足的条件: 返回下一页上一页 围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角时,就拼成一个平面图形。就说它们能拼地板。在交流中达成共识 概括:结论:返回下一页上一页(1)正三角形与正方形注意:同一个组合会有不同的密铺结果图例:返回下一页上一页(2)正三角形与正六边形注意:同一个组合会有不同的密铺结果图例:返回下一页上一页(3)正方形与正八边形图例:思考:还有其它的组合吗?返回下一页上一页正五边形、正十边形围绕一点能拼成360o,但能扩展到整个平面,即铺满地面吗?尽管能围绕一点拼成360o,但不能扩展到整个平面。(4)三种正多边形的平面密铺正十二边形与正方形、正六边形的平面密铺正六边形与正方形、正三角形的平面密铺
图例:返回下一页上一页1.商店出售下列形状的地砖:⑴正三角形⑵正方形⑶正五边形
(4)正六边形,若只选购其中某一种地砖铺满地面,可供选
择的地砖共有( )
A.1种 B. 2种 C. 3种 D. 4种
2.能够铺满地面的边长都相等的正多边形的组合是( )
A.正三角形和正方形 B. 正方形和正六边形
C.正三角形和正十二边形 D. 正三角形、正方形和正六边形
3.下列图形组合中,能够铺满地面的是( )
A.任意一种三角形和任意一种四边形
C.任意一种三角形和任意一种梯形 D.正八边形和等腰直角三角形
练习:CACDC返回下一页上一页选择题(可能有多个答案)B.正五边形和正十边形用正五边形和什么多边形能铺满地板?延伸探究:返回下一页上一页 1.平面图形的密铺指没有空隙和不重叠的拼接; 2.用一种或多种正多边形铺满地面的关键是:围绕一点拼在一起的几个内角加在一起恰好组成一个周角,这是多边形铺满地面的必须条件。3.有那些图形能组成平面密铺本节课你有什么收获?小结:发现二:
发现一:
同一种多边形进行平面密铺的图形只有三种:三角形、四边形、正六边形多种多边形能进行平面密铺的条件是:(1)拼接在同一点的各个角的度数和是360度(2)相邻的多边形有公共边返回下一页上一页(正五边形和正十边形是例外)图案欣赏3.有那些图形能组成平面密铺返回图案欣赏:返回下一页上一页密铺在现实生活中应用非常广泛.图案欣赏:图案欣赏: 图案欣赏:图案欣赏:图案欣赏:图案欣赏:图案欣赏:图案欣赏:图案欣赏:祝同学们
学习进步再见返回?
