6.3 余角 补角 对顶角

课件16张PPT。奋进的阜宁县实验初中欢迎您 阜宁县实验初中初一数学组 曹衍§6.3 余角与补角观察与思考其中的一个角叫做另一个角的余角。∠α+ ∠ β=900
∠α=900- ∠ β
∠ β=900- ∠α∠α与 ∠ β的度数之间有什么特殊关系？ 如果两个角的和是一个平角，这两个角叫做互为补角，简称互补。其中的一个角叫做另一个角的补角。观察与思考∠α+ ∠ β=1800
∠α=1800- ∠ β
∠ β=1800- ∠α∠α与 ∠ β的度数之间有什么特殊关系？判断：
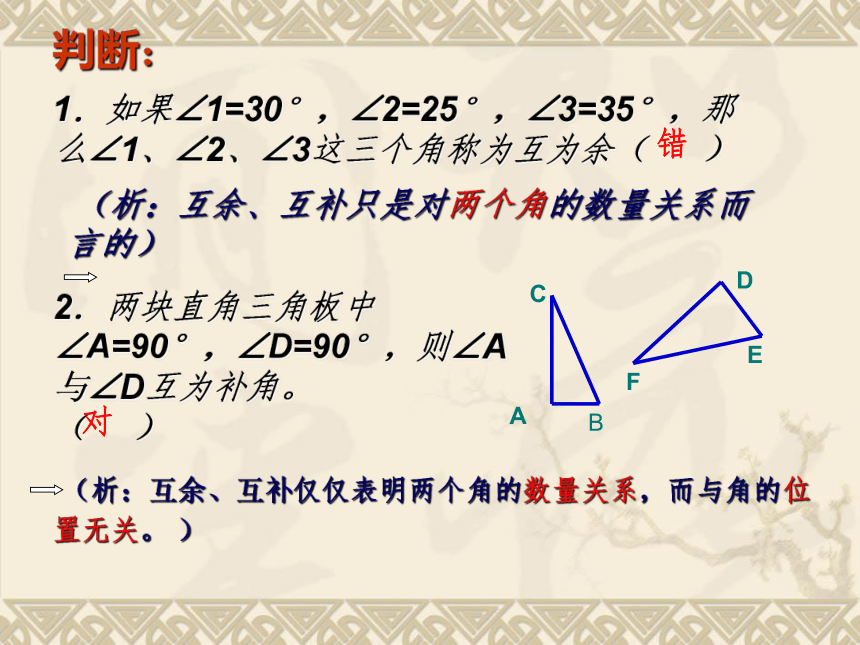
1．如果∠1=30°，∠2=25°，∠3=35°，那么∠1、∠2、∠3这三个角称为互为余（ ）错 （析：互余、互补只是对两个角的数量关系而言的）2．两块直角三角板中∠A=90°，∠D=90°，则∠A与∠D互为补角。
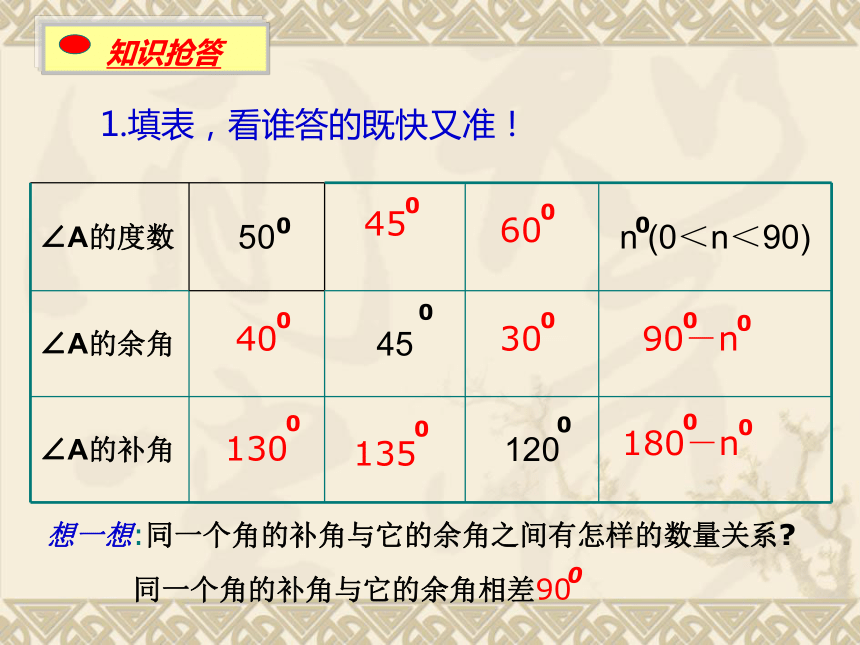
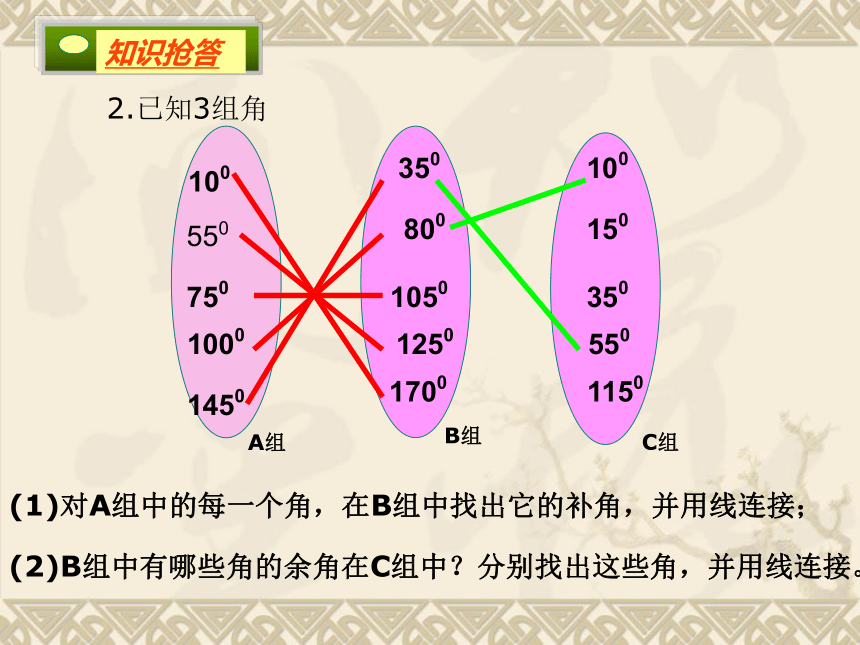
（ ） 对 （析：互余、互补仅仅表明两个角的数量关系，而与角的位置无关。 ）1.填表，看谁答的既快又准！0000想一想:同一个角的补角与它的余角之间有怎样的数量关系?A组B组1005507501000145035080010501250170010015035055011502.已知3组角(1)对A组中的每一个角，在B组中找出它的补角，并用线连接；(2)B组中有哪些角的余角在C组中？分别找出这些角，并用线连接。C组 已知一个角的补角是这个角的余角的4倍，求这个角的度数。解：设这个角为x°，则它的余角为(90-x) °，它的补角为(180-x) °，得180-x=4(90-x) 180-x=360-4x -x+4x=360-18 3x=180 X=60答：这个角是60o。同角的余角相等；
理由：∵∠1与∠ 2互余， ∠1与∠3互余，
∴∠ 2＝ 90 ° － ∠1， ∠3＝ 90 ° － ∠1
∴∠2＝∠3解： ∠2与∠3相等.同角的补角相等；
理由：∵∠1与∠ 2互补， ∠1与∠3互补，
∴∠ 2＝ 180 ° － ∠1， ∠3＝ 180 ° － ∠1
∴∠2＝∠3解： ∠2与∠3相等.如果把互余改为互补， ∠2与∠4仍相等吗?想一想同角（或等角）的余角相等。
同角（或等角）的补角相等。 理由:∵∠1与∠2互余 ∴∠2=90o-∠1 ∵∠3与∠4互余 ∴∠4=90o-∠3 又∵∠1=∠3 ∴∠2=∠4（等量减等量差相等）解： ∠2与∠4相等性质：同角（或等角）的余角相等。
同角（或等角）的补角相等。几何语言：
∵ ∠1+ ∠ 2=900
∠ 1+ ∠ 3 = 900
∴ ∠ 2 = ∠ 3
（同角的余角相等）几何语言：
∵ ∠1+ ∠ 2=900
∠ 3+ ∠ 4 = 900
又∵ ∠ 1 = ∠ 3
∴ ∠ 2 = ∠ 4
（等角的余角相等）2.如图，∠1+∠2=180，∠1+∠3=180，∠2与∠3的大小关系是_________，理由：_______________.∠A=∠BCD同角的余角相等∠2=∠3同角的补角相等 如图，O是直线AB上的一点，OC平分∠AOB，∠DOE=90o，则
（1）∠2=∠（ ），∠1=∠（ ）
（2）图中，互为余角的角共有哪几对？
（ ）
（3）图中，∠DOB的补角是 。 4 3 ∠1与∠2，∠1与∠4，∠2与∠3，∠4与∠3 ∠1，∠3（4）延长EO到F，∠COF与∠ BOD的大小关系怎样？解： ∠COF=∠ BOD
理由：∵ ∠COF+∠ 3=1800
∠ BOD+∠1=1800
又∵∠ 1 = ∠3
∴ ∠COF=∠ BOD思维拓展知识就象一艘船
让它载着你
驶向你理想的彼岸今天我们学到了什么?你能说出来吗?课 堂 小 结课堂检测１.如果∠１＝∠２，∠２＝∠３，那么∠１　∠３；　如果∠１＞∠２，∠２＞∠３，那么∠１　　∠３。3.如图，直线CD经过点O，且OC平分∠AOB。∠AOD与∠BOD有怎样的大小关系？说明你的理由。
2．已知∠B是它补角的3倍，求∠B的度数。谢谢各位专家的光临与指导再见