北师大版高中数学必修2课件-2.2.3直线与圆方程的应用 (共12张PPT)
文档属性
| 名称 | 北师大版高中数学必修2课件-2.2.3直线与圆方程的应用 (共12张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 476.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-25 13:45:27 | ||
图片预览




文档简介
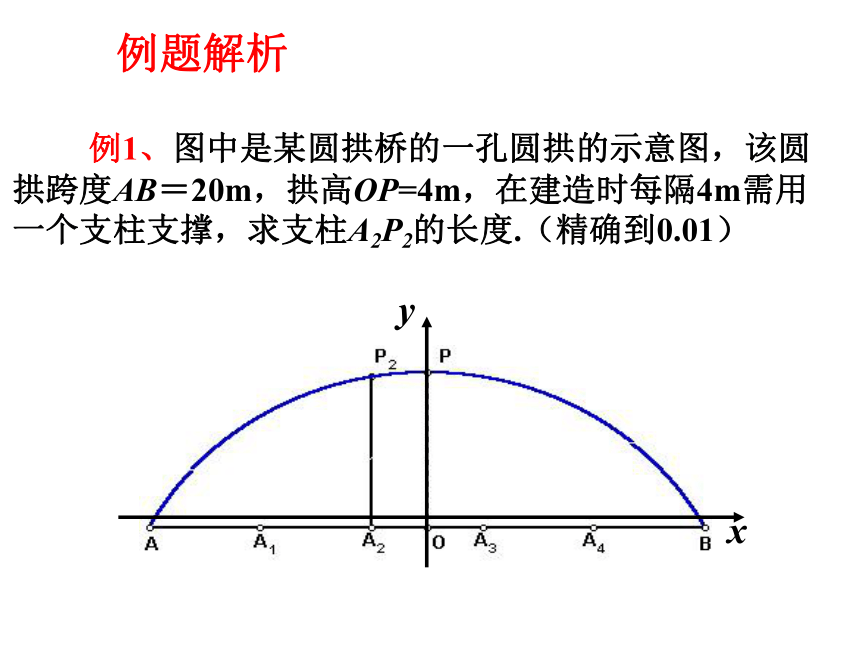
课件12张PPT。2.2.3 直线与圆方程的应用 例1、图中是某圆拱桥的一孔圆拱的示意图,该圆拱跨度AB=20m,拱高OP=4m,在建造时每隔4m需用一个支柱支撑,求支柱A2P2的长度.(精确到0.01)例题解析y例题解析 思考:(用坐标法)
1.圆心和半径能直接求出吗?
2.怎样求出圆的方程?
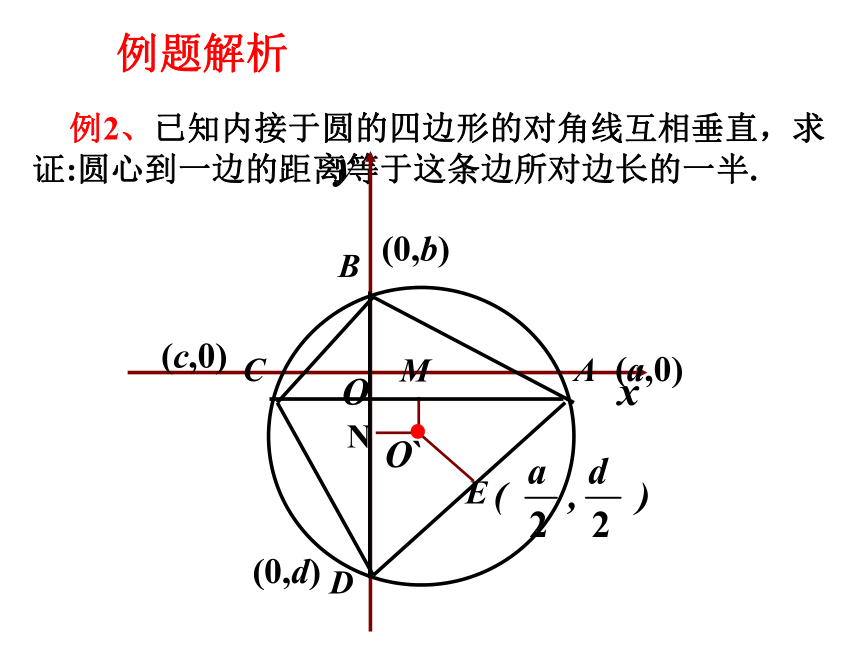
3.怎样求出支柱A2P2的长度?解:建立如图所示的坐标系,设圆心坐标是(0,b),圆的半径是r ,则圆的方程是x2+(y-b)2=r2 .把P(0,4), B(10,0)代入圆的方程得方程组:解得,b= -10.5 , r2=14.52所以圆的方程是: x2+(y+10.5)2=14.52把点P2的横坐标x= -2 代入圆的方程,得 (-2)2+(y+10.5)2=14.52因为y>0,所以y=答:支柱A2P2的长度约为3.86m.例题解析E 例2、已知内接于圆的四边形的对角线互相垂直,求证:圆心到一边的距离等于这条边所对边长的一半.(a,0)(0,b)(c,0)(0,d)例题解析解:以四边形ABCD互相垂直的对角线作为x轴y轴,建立直角坐标系,设 A(a,0),B(0,b),C(c,0),D(0,d)过四边形的外接圆圆心O’作AC、BD、AD边的垂线,垂足为M、N、E,则M、N、E分别为AC、BD、AD边的中点.由线段的中点坐标公式有:例题解析例题解析用坐标法解决平面几何问题的步骤:第一步:建立适当的坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;第二步:通过代数运算,解决代数问题;第三步:把代数运算结果“翻译”成几何结论.课内小结1. 求直线l: 2x-y-2=0被圆C: (x-3)2+y2=9所截得的弦长.课内练习课内练习 理解直线与圆的位置关系的几何性质;
利用平面直角坐标系解决直线与圆的位置关系;
熟悉直线与方程的关系,并应用其解决相关问题;
会用“数形结合”的数学思想解决问题.课堂小结 课本P98复习题C组 3课后作业
1.圆心和半径能直接求出吗?
2.怎样求出圆的方程?
3.怎样求出支柱A2P2的长度?解:建立如图所示的坐标系,设圆心坐标是(0,b),圆的半径是r ,则圆的方程是x2+(y-b)2=r2 .把P(0,4), B(10,0)代入圆的方程得方程组:解得,b= -10.5 , r2=14.52所以圆的方程是: x2+(y+10.5)2=14.52把点P2的横坐标x= -2 代入圆的方程,得 (-2)2+(y+10.5)2=14.52因为y>0,所以y=答:支柱A2P2的长度约为3.86m.例题解析E 例2、已知内接于圆的四边形的对角线互相垂直,求证:圆心到一边的距离等于这条边所对边长的一半.(a,0)(0,b)(c,0)(0,d)例题解析解:以四边形ABCD互相垂直的对角线作为x轴y轴,建立直角坐标系,设 A(a,0),B(0,b),C(c,0),D(0,d)过四边形的外接圆圆心O’作AC、BD、AD边的垂线,垂足为M、N、E,则M、N、E分别为AC、BD、AD边的中点.由线段的中点坐标公式有:例题解析例题解析用坐标法解决平面几何问题的步骤:第一步:建立适当的坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;第二步:通过代数运算,解决代数问题;第三步:把代数运算结果“翻译”成几何结论.课内小结1. 求直线l: 2x-y-2=0被圆C: (x-3)2+y2=9所截得的弦长.课内练习课内练习 理解直线与圆的位置关系的几何性质;
利用平面直角坐标系解决直线与圆的位置关系;
熟悉直线与方程的关系,并应用其解决相关问题;
会用“数形结合”的数学思想解决问题.课堂小结 课本P98复习题C组 3课后作业
