1.2 轴对称的性质

课件11张PPT。轴对称的性质基础训练1.若线段AB和A′B′关于直线l对称,
则AB=A′B′ ( )
2.若线段AB和A′B′在直线l的两旁,且AB=A′B′,则线段AB和A′B′关于直线l对称( )
3.若点A与A′到直线l的距离相等,则若点A与A′关于直线l对称 ( )
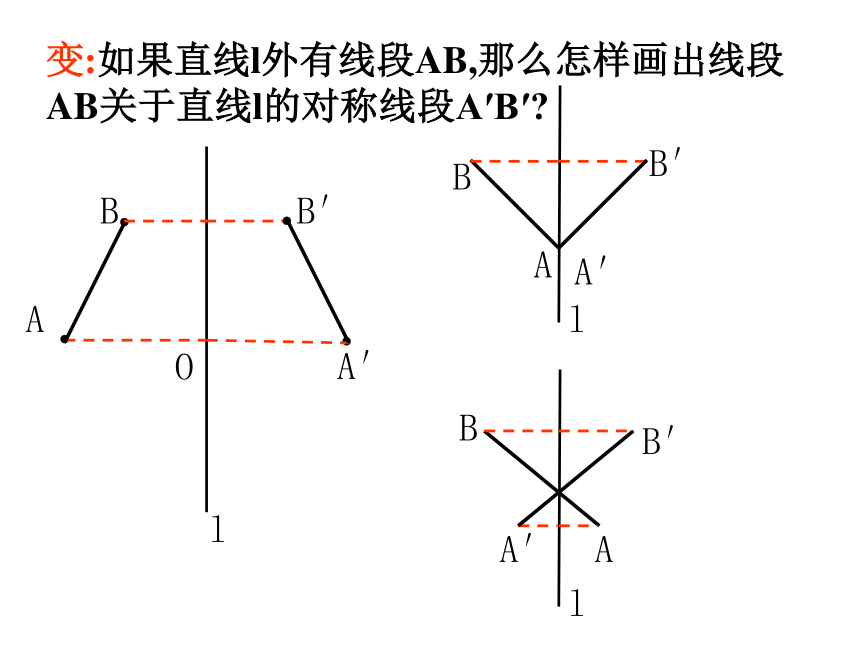
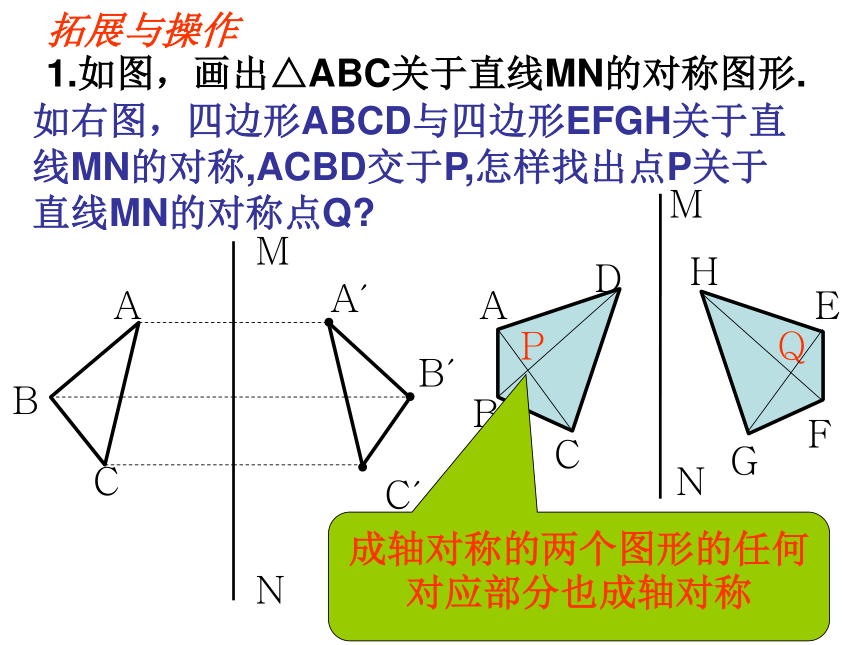
4.若△ABC≌△A′B′C′,则△ABC和△A′B′C′,关于某直线对称 ( )√×××(一)判断(二)如果直线l外有一点A,那么怎样画出点A关于直线l的对称点A′?●●AA′lO┏变:如果直线l外有线段AB,那么怎样画出线段AB关于直线l的对称线段A′B′?●●AA′lOB●●B′A′B′A′B′1.如图，画出△ABC关于直线MN的对称图形.AA′CBB′C′NM●●●NMACBFEDHPGQ如右图，四边形ABCD与四边形EFGH关于直线MN的对称,ACBD交于P,怎样找出点P关于直线MN的对称点Q?成轴对称的两个图形的任何对应部分也成轴对称拓展与操作2.下图是由半圆和三角形组成的图形,请以AB为对称轴,作出图形的另一半(用尺规作图,保留作图痕迹)●AB3.为创建文明城,建湖某居民小区搞绿化,要在一块矩形空地上建花坛,现征集设计方案,要求设计的图案由圆和正方形组成(圆与正方形的个数不限),并使整个矩形场地成轴对称图形.试试看:见书P13 1-2 如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD，且AC=BD，若A到河岸CD的中点的距离为500m,若牧童从A处将牛牵到河边饮水后再回家，试问在何处饮水，所走路程最短？最短路程是多少？ADCBNMA′1000m迁移与应用变:如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC、BD，且AC≠BD，若牧童从A处将牛牵到河边饮水后再回家，试问在何处饮水，所走路程最短？ADCBMA′变:如图，已知，∠AOB内有一点P，求作△PQR，使Q在OA 上，R在OB上，且使△PQR的周长最小.P′P″RQ课堂作业:见书P15 2、5再见