人教版七年级数学上册3.2解一元一次方程(一)——合并同类项与移项第二课时课件 (共17张PPT)
文档属性
| 名称 | 人教版七年级数学上册3.2解一元一次方程(一)——合并同类项与移项第二课时课件 (共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 304.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-25 00:00:00 | ||
图片预览






文档简介
课件17张PPT。3.2解一元一次方程(一)
——合并同类项与移项
第二课时移项
复习:1.解下列方程:(1)
(2) 2.用合并同类项解一元一次方程的步骤.1.解:(1)
合并同类项,得
系数化为1,得
(2)
合并同类项,得
系数化为1,得
2.合并同类项,系数化为1.情境引入问题1:把一些图书分给某班学生阅 读,如果每人分3本,则剩余20本;如果每人分4本。则还缺25本.这个班有多少学生?这批书的总数有几种
表示法?
它们之间有什么关系?分析:
设这个班有 名学生,那么
每人分3本时,图书总数是 ;
每人分4本时,图书总是 .
则可列方程 = .这批书的总数是一个定值方程 的两边都有含 的项( 与 )和不含字母的常数项(20与-25)怎样过能使它向 ( 常数)的形式转 化呢?问题2:分析:
为了使右边不含 的项,所以右边要减去 ,根据等式的性质 左边也要减去 ;
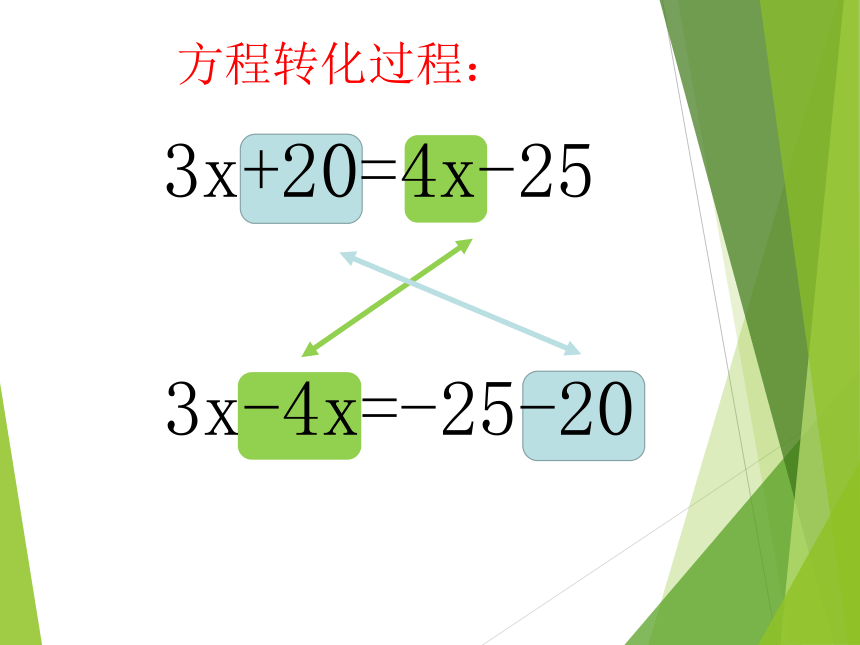
为了使左边不含常数项,所以左边要减去 ,根据等式的性质 ,右边也要减去 ,则方程可转化为 .方程转化过程:3x+20=4x-253x-4x=-25-20象上面那样,把等式一边的某项变号后移到另一边,叫做移项.问题3:上面解方程中“移项”起了什么作用?通过移项,含未知数的项与常数项分别位于方程左右两边,使方程更接近于 的形式.
解方程时经常要“合并同类项”和“移项”,前面提到古老的代数书中的“对消”和“还原”,指的就是“合并同类项”和“移项”.早在一千多年前,数学家阿尔——花拉子米就已经对“合并同类项”和“移项”非常重视了.范例学习例3解下列方程:(1) ;
(2) .解:(1)移项,得
合并同类项,得
系数化为1,得
(2)移项,得
合并同类项,得
系数化为1,得
例4某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200 t;如用新工艺,则废水排量比环保限制的最大量少100 t. 新旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少?范例学习分析:设新工艺废水排量为 t,
由用旧工艺可得环保限制的最大量可用式子表示
为 ;
由用新工艺可得环保限制的最大量可用式子表示
为 .这两个式子是什么关系?解:设新、旧工艺的废水排量分别为 t和 t.
根据废水排量与环保限制最大量之间的关系,得移项,得合并同类项,得系数化为1,得所以答:新、旧工艺产生的废水排量分别为200 t和500 t.利用表示同一个量的式子相等列方程巩固拓展1.解下列方程:
(1) ;
(2) .1.解:(1)移项得,
,
合并同类项,得
,
系数化为1,得
(2)移项,得
,
合并同类项,得
,
系数化为1,得
.巩固拓展2.王芳和李丽同时采摘樱桃,王芳平均每小时采摘8kg,李丽平均每小时采摘7kg.采摘结束后王芳从她采摘的樱桃中取出0.25kg给了李丽,这时两人的樱桃一样多.她们采摘用了多少时间?2.解:设她们采摘用了 个小时.
列方程,得
移项,得
合并同类项,得
答:她们采摘用了0.5小时.课堂小结1.本节课主要学习了解一元一次方程的方
法:移项,移项的根据是等式的性质1.
2.本节的实际问题的相等关系的依据:表示同一个量的两个式子相等.
3.列方程解实际问题的基本思路.作业:
教科书第91页习题3.2第3、6题
(2) 2.用合并同类项解一元一次方程的步骤.1.解:(1)
合并同类项,得
系数化为1,得
(2)
合并同类项,得
系数化为1,得
2.合并同类项,系数化为1.情境引入问题1:把一些图书分给某班学生阅 读,如果每人分3本,则剩余20本;如果每人分4本。则还缺25本.这个班有多少学生?这批书的总数有几种
表示法?
它们之间有什么关系?分析:
设这个班有 名学生,那么
每人分3本时,图书总数是 ;
每人分4本时,图书总是 .
则可列方程 = .这批书的总数是一个定值方程 的两边都有含 的项( 与 )和不含字母的常数项(20与-25)怎样过能使它向 ( 常数)的形式转 化呢?问题2:分析:
为了使右边不含 的项,所以右边要减去 ,根据等式的性质 左边也要减去 ;
为了使左边不含常数项,所以左边要减去 ,根据等式的性质 ,右边也要减去 ,则方程可转化为 .方程转化过程:3x+20=4x-253x-4x=-25-20象上面那样,把等式一边的某项变号后移到另一边,叫做移项.问题3:上面解方程中“移项”起了什么作用?通过移项,含未知数的项与常数项分别位于方程左右两边,使方程更接近于 的形式.
解方程时经常要“合并同类项”和“移项”,前面提到古老的代数书中的“对消”和“还原”,指的就是“合并同类项”和“移项”.早在一千多年前,数学家阿尔——花拉子米就已经对“合并同类项”和“移项”非常重视了.范例学习例3解下列方程:(1) ;
(2) .解:(1)移项,得
合并同类项,得
系数化为1,得
(2)移项,得
合并同类项,得
系数化为1,得
例4某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200 t;如用新工艺,则废水排量比环保限制的最大量少100 t. 新旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少?范例学习分析:设新工艺废水排量为 t,
由用旧工艺可得环保限制的最大量可用式子表示
为 ;
由用新工艺可得环保限制的最大量可用式子表示
为 .这两个式子是什么关系?解:设新、旧工艺的废水排量分别为 t和 t.
根据废水排量与环保限制最大量之间的关系,得移项,得合并同类项,得系数化为1,得所以答:新、旧工艺产生的废水排量分别为200 t和500 t.利用表示同一个量的式子相等列方程巩固拓展1.解下列方程:
(1) ;
(2) .1.解:(1)移项得,
,
合并同类项,得
,
系数化为1,得
(2)移项,得
,
合并同类项,得
,
系数化为1,得
.巩固拓展2.王芳和李丽同时采摘樱桃,王芳平均每小时采摘8kg,李丽平均每小时采摘7kg.采摘结束后王芳从她采摘的樱桃中取出0.25kg给了李丽,这时两人的樱桃一样多.她们采摘用了多少时间?2.解:设她们采摘用了 个小时.
列方程,得
移项,得
合并同类项,得
答:她们采摘用了0.5小时.课堂小结1.本节课主要学习了解一元一次方程的方
法:移项,移项的根据是等式的性质1.
2.本节的实际问题的相等关系的依据:表示同一个量的两个式子相等.
3.列方程解实际问题的基本思路.作业:
教科书第91页习题3.2第3、6题
