人教版数学九年级上册24.2.1 点和圆的位置关系课件
文档属性
| 名称 | 人教版数学九年级上册24.2.1 点和圆的位置关系课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-24 18:43:32 | ||
图片预览





文档简介
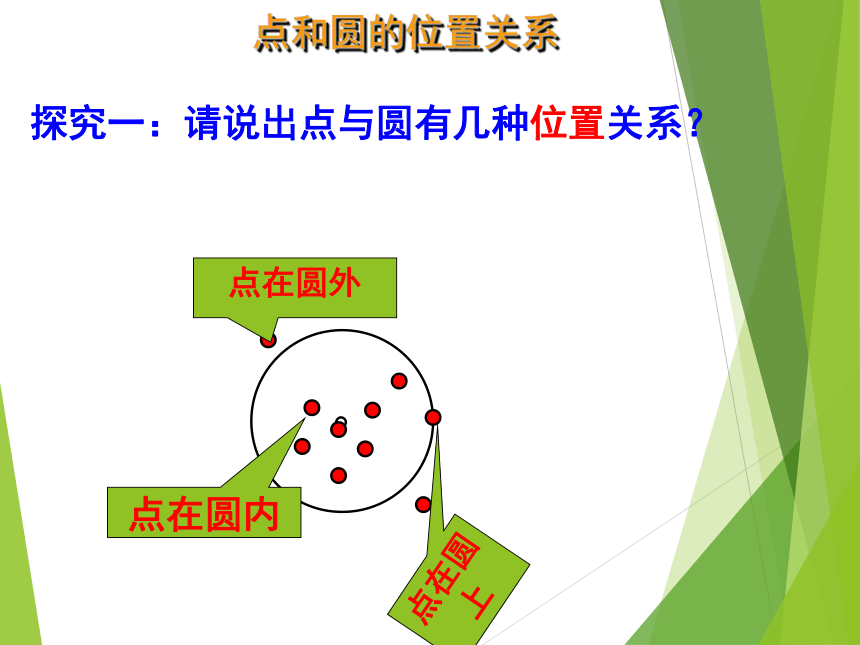
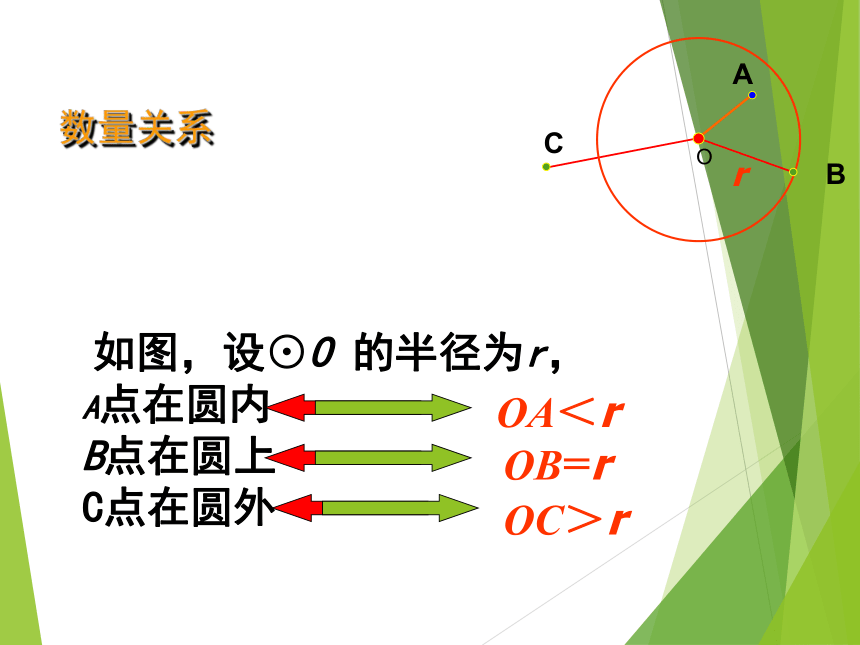
课件25张PPT。24.2.1 点和圆的位置关系你看过射击比赛吗? 射箭是奥运会的一个正式体育项目,我国射箭运动员在奥运会上屡获金牌,为我国赢得了荣誉,如图是一个运动员打靶用的靶环,它是由若干个同心圆组成的.你知道射中靶子上不同位置的成绩是怎样计算的吗?探究一:请说出点与圆有几种位置关系? 点在圆外点在圆上点在圆内点和圆的位置关系 如图,设⊙O 的半径为r,
A点在圆内
B点在圆上
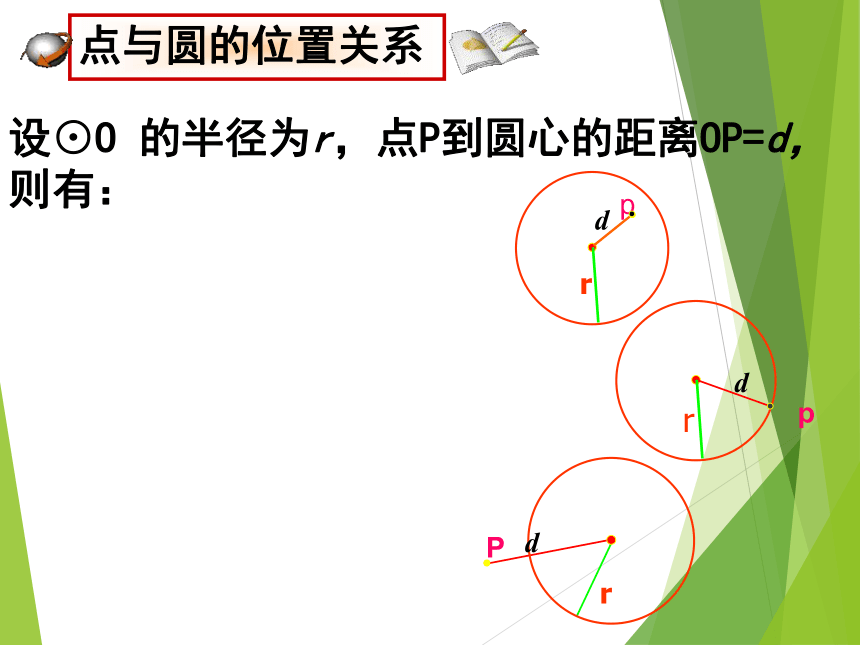
C点在圆外 OA<r OB=r OC>rO数量关系设⊙O 的半径为r,点P到圆心的距离OP=d,则有:d例1:⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:
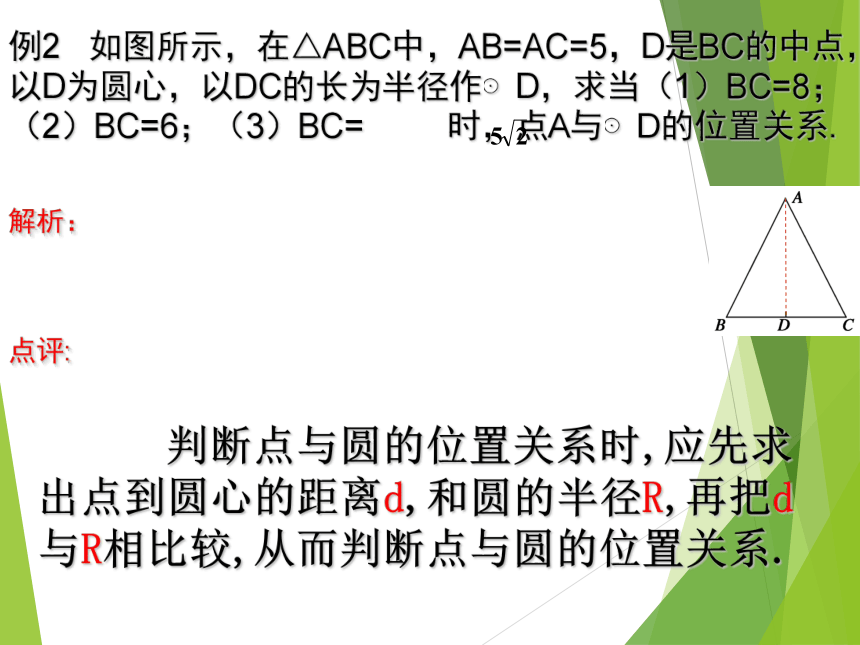
我会做点和圆的位置关系解析:在Rt△ADC中,AD= = =3. 判断点与圆的位置关系时,应先求出点到圆心的距离d,和圆的半径R,再把d与R相比较,从而判断点与圆的位置关系.点评:例2 如图所示,在△ABC中,AB=AC=5,D是BC的中点,以D为圆心,以DC的长为半径作⊙D,求当(1)BC=8;(2)BC=6;(3)BC= 时,点A与⊙D的位置关系.二、探究与实践你会画圆吗? 1、平面上有一点A,经过已知A点的圆有几个?圆心在哪里? ●A 无数个,圆心为点A以外任意一点,半径为这点与点A的距离 2、平面上有两点A、B,经过已知点A、B的圆有几个?它们的圆心分布有什么特点? 以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.无数个。它们的圆心都在线段AB的垂直平分线上。 3、平面上有三点A、B、C,经过A、B、C三点的圆有几个?圆心在哪里? ●B●C经过B,C两点的圆的圆心在线段AB的垂直平分线上.●A经过A,B,C三点的圆的圆心应该这两条垂直平分线的交点O的位置.●O经过A,B两点的圆的圆心在线段AB的垂直平分线上.这样的圆可以做多少个?归纳结论: 经过三角形三个顶点可以画一个圆,并且只能画一个.经过三角形三个顶点的圆叫做三角形的外接圆。这个三角形叫做这个圆的内接三角形。三角形外接圆的圆心叫做这个三角形的外心。●O 例3、如图,在坐标网格图中,△ABC外心的坐标是 .巩固练习能力提升例4.若O为△ABC的外心,∠BOC=60°,求∠BAC的度数。练习1.如图,已知三角形ABC中,AB=6cm,BC=8cm,AC=10cm,求△ABC的外接圆半径 练习2.如图,已知等边三角形ABC中,边长为6cm,求它的外接圆半径。探究三你会解答前面的疑问吗?(2)经过同一条直线三个点能作出一个圆吗? 假设过同一条直线l上三点A、B、C可以作一个圆 设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点, 这与 “过一点有且只有一条直线与已知直线垂直”相矛盾, 所以过同一条直线上的三点不能作圆.
什么叫反证法? 反证法:
假设命题的结论不正确,由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立,这种方法叫做反证法.
步骤:
(1)假设命题的结论不成立;
(2)推理得出矛盾;
(3)结论成立.你会用反证法吗?用反证法证明:在一个三角形中,至少有一个内角小于或等于60°.
已知:△ABC,
求证:△ABC中至少有一个内角小于或等于60°.即∠A>60°,∠B>60°,∠C>60°, 于是∠A+∠B+∠C>60°+60°+60°=180°,这与三角形的内角和等于180°相矛盾. 证明:假设△ABC中没有一个内角小于或等于60°, 用反证法证明命题时,
1、先假设命题的结论不成立,
2、根据“假设”得出与定义、定理、公理或已知条件相矛盾的结论,
3、由此说明“假设”不成立,从而证明原命题结论是正确的.思路:所以△ABC中至少有一个内角小于或等于60°.小结与归纳◆用数量关系判断点和圆的位置关系。
◆不在同一直线上的三点确定一个圆。◆求解特殊三角形直角三角形、等边三角形、
等腰三角形的外接圆半径。课后思考:经过四个点是不是可以作一圆?再见
A点在圆内
B点在圆上
C点在圆外 OA<r OB=r OC>rO数量关系设⊙O 的半径为r,点P到圆心的距离OP=d,则有:d例1:⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:
我会做点和圆的位置关系解析:在Rt△ADC中,AD= = =3. 判断点与圆的位置关系时,应先求出点到圆心的距离d,和圆的半径R,再把d与R相比较,从而判断点与圆的位置关系.点评:例2 如图所示,在△ABC中,AB=AC=5,D是BC的中点,以D为圆心,以DC的长为半径作⊙D,求当(1)BC=8;(2)BC=6;(3)BC= 时,点A与⊙D的位置关系.二、探究与实践你会画圆吗? 1、平面上有一点A,经过已知A点的圆有几个?圆心在哪里? ●A 无数个,圆心为点A以外任意一点,半径为这点与点A的距离 2、平面上有两点A、B,经过已知点A、B的圆有几个?它们的圆心分布有什么特点? 以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.无数个。它们的圆心都在线段AB的垂直平分线上。 3、平面上有三点A、B、C,经过A、B、C三点的圆有几个?圆心在哪里? ●B●C经过B,C两点的圆的圆心在线段AB的垂直平分线上.●A经过A,B,C三点的圆的圆心应该这两条垂直平分线的交点O的位置.●O经过A,B两点的圆的圆心在线段AB的垂直平分线上.这样的圆可以做多少个?归纳结论: 经过三角形三个顶点可以画一个圆,并且只能画一个.经过三角形三个顶点的圆叫做三角形的外接圆。这个三角形叫做这个圆的内接三角形。三角形外接圆的圆心叫做这个三角形的外心。●O 例3、如图,在坐标网格图中,△ABC外心的坐标是 .巩固练习能力提升例4.若O为△ABC的外心,∠BOC=60°,求∠BAC的度数。练习1.如图,已知三角形ABC中,AB=6cm,BC=8cm,AC=10cm,求△ABC的外接圆半径 练习2.如图,已知等边三角形ABC中,边长为6cm,求它的外接圆半径。探究三你会解答前面的疑问吗?(2)经过同一条直线三个点能作出一个圆吗? 假设过同一条直线l上三点A、B、C可以作一个圆 设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,即点P为l1与l2的交点, 这与 “过一点有且只有一条直线与已知直线垂直”相矛盾, 所以过同一条直线上的三点不能作圆.
什么叫反证法? 反证法:
假设命题的结论不正确,由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立,这种方法叫做反证法.
步骤:
(1)假设命题的结论不成立;
(2)推理得出矛盾;
(3)结论成立.你会用反证法吗?用反证法证明:在一个三角形中,至少有一个内角小于或等于60°.
已知:△ABC,
求证:△ABC中至少有一个内角小于或等于60°.即∠A>60°,∠B>60°,∠C>60°, 于是∠A+∠B+∠C>60°+60°+60°=180°,这与三角形的内角和等于180°相矛盾. 证明:假设△ABC中没有一个内角小于或等于60°, 用反证法证明命题时,
1、先假设命题的结论不成立,
2、根据“假设”得出与定义、定理、公理或已知条件相矛盾的结论,
3、由此说明“假设”不成立,从而证明原命题结论是正确的.思路:所以△ABC中至少有一个内角小于或等于60°.小结与归纳◆用数量关系判断点和圆的位置关系。
◆不在同一直线上的三点确定一个圆。◆求解特殊三角形直角三角形、等边三角形、
等腰三角形的外接圆半径。课后思考:经过四个点是不是可以作一圆?再见
同课章节目录
