人教版数学九年级上册24.2.2切线的性质与判定课件
文档属性
| 名称 | 人教版数学九年级上册24.2.2切线的性质与判定课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-24 00:00:00 | ||
图片预览







文档简介
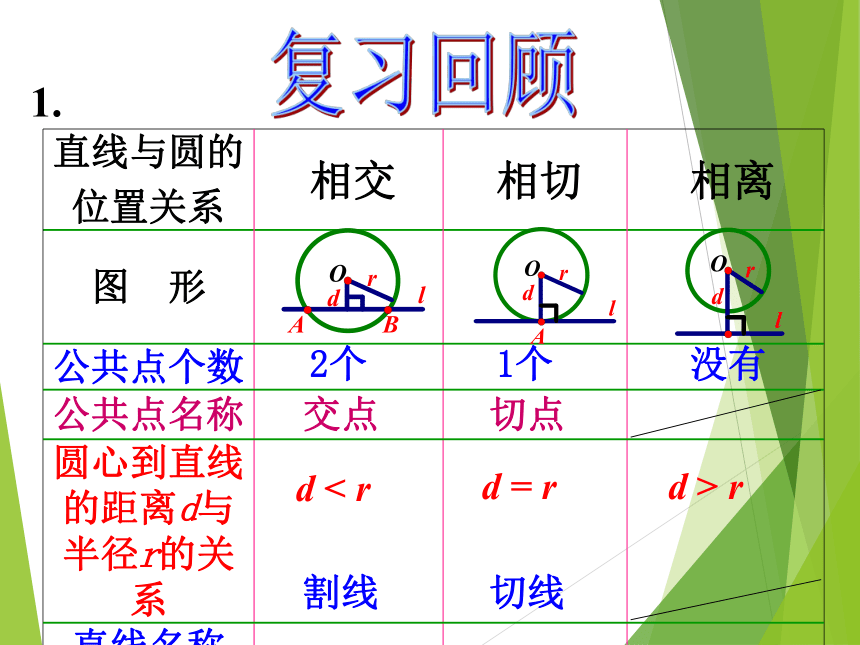
课件21张PPT。24.2.2直线和圆的位置关系(第2课时)人民教育出版社九年级上册 2个交点1个切点d < rd = rd > r没有1.割线切线相交相切相离复习回顾1.复习回顾 2.判断直线与圆相切有哪些方法?l方法1:直线与圆只有一个公共点;方法2:圆心到直线的距离等于半径. 复习回顾学习目标(1)圆心O到直线l的距离d与r的关系是
d=r
(2)直线l和⊙O有什么位置关系?
相切如图,⊙O的半径为r,在⊙O上任意取一点A,连接OA,过点A作直线l⊥OA当直线l满足什么条件时,直线l与⊙O相切?探究一经过半径的外端并且垂直
于这条半径的直线是圆的切线.切线的判定定理:探究一请你判断下列说法是否正确:
(1)过半径的外端的直线是圆的切线( )
(2)与半径垂直的直线是圆的切线( )
(3)过半径的端点并且与半径垂直的直线
是圆的切线( )× ××切线必须同时满足两条:
①经过半径外端;
②垂直于这条半径.两个条件缺一不可跟踪练习如图,⊙O的半径为r,
答:OA⊥l ,假设OA与直线l不垂直
则OA不是点O到直线l的垂线段
过点O作OM⊥l于点M
OM的长为点O到直线l的距离d
根据垂线段最短的性质,
有OM与已知矛盾
故假设不成立 ,那么半径OA与直线l是不是一定垂直呢?为什么?如果直线l是⊙O的切线,切点为A圆的切线垂直于过切点的半径切线的性质定理探究二①过半径外端
②垂直于这条半径切线①圆的切线
②过切点的半径垂直切线判定定理:切线性质定理:比较已知:直线AB经过⊙O上的点C,并且OA=OB,
CA=CB.求证:直线AB是⊙O的切线.已知:如图,△ABC为等腰三角形,O是底边
BC的中点,腰AB与⊙O相切于点 D.求证:AC
是⊙O的切线.问题1.问题2.公共点已知,连半径,证垂直公共点未知,作垂直,证半径1.证切线2.已知切线连半径,得垂直合作,交流,展示归纳1.如图,PA切⊙O于点A,该圆的半径为3,PO=5,
则PA的长等于______.42.如图,A,B是⊙O上的两点, AC是⊙O的切线,
∠B=70°,则∠BAC=________.目标检测20°3.如图,在△ABC中,∠A=∠B=30°,点O在AB上,⊙O经过点A、点D,与AB交于点C.求证:BD是⊙O的切线.第1题图第2题图第3题图3.如图,在△ABC中,∠A=∠B=30°,点O在AB上,⊙O经过点A、点D,与AB交于点C.求证:BD是⊙O的切线.目标检测1.切线的判定定理:
经过半径的外端并且垂直于这条半径的直
线是圆的切线.2.切线的性质定理:
圆的切线垂直于过切点的半径. 公共点已知,连半径,证垂直
公共点未知,作垂直,证半径连接圆心和切点,得到半径,则半径垂直于切线小结请你谈谈今天有哪些收获?选做题
实践调查:寻找圆与直线的位置
关系在实际生活中的应用.必做题
课本98页练习题1;
课本101页习题5,12.作业谢谢大家!
d=r
(2)直线l和⊙O有什么位置关系?
相切如图,⊙O的半径为r,在⊙O上任意取一点A,连接OA,过点A作直线l⊥OA当直线l满足什么条件时,直线l与⊙O相切?探究一经过半径的外端并且垂直
于这条半径的直线是圆的切线.切线的判定定理:探究一请你判断下列说法是否正确:
(1)过半径的外端的直线是圆的切线( )
(2)与半径垂直的直线是圆的切线( )
(3)过半径的端点并且与半径垂直的直线
是圆的切线( )× ××切线必须同时满足两条:
①经过半径外端;
②垂直于这条半径.两个条件缺一不可跟踪练习如图,⊙O的半径为r,
答:OA⊥l ,假设OA与直线l不垂直
则OA不是点O到直线l的垂线段
过点O作OM⊥l于点M
OM的长为点O到直线l的距离d
根据垂线段最短的性质,
有OM
故假设不成立 ,那么半径OA与直线l是不是一定垂直呢?为什么?如果直线l是⊙O的切线,切点为A圆的切线垂直于过切点的半径切线的性质定理探究二①过半径外端
②垂直于这条半径切线①圆的切线
②过切点的半径垂直切线判定定理:切线性质定理:比较已知:直线AB经过⊙O上的点C,并且OA=OB,
CA=CB.求证:直线AB是⊙O的切线.已知:如图,△ABC为等腰三角形,O是底边
BC的中点,腰AB与⊙O相切于点 D.求证:AC
是⊙O的切线.问题1.问题2.公共点已知,连半径,证垂直公共点未知,作垂直,证半径1.证切线2.已知切线连半径,得垂直合作,交流,展示归纳1.如图,PA切⊙O于点A,该圆的半径为3,PO=5,
则PA的长等于______.42.如图,A,B是⊙O上的两点, AC是⊙O的切线,
∠B=70°,则∠BAC=________.目标检测20°3.如图,在△ABC中,∠A=∠B=30°,点O在AB上,⊙O经过点A、点D,与AB交于点C.求证:BD是⊙O的切线.第1题图第2题图第3题图3.如图,在△ABC中,∠A=∠B=30°,点O在AB上,⊙O经过点A、点D,与AB交于点C.求证:BD是⊙O的切线.目标检测1.切线的判定定理:
经过半径的外端并且垂直于这条半径的直
线是圆的切线.2.切线的性质定理:
圆的切线垂直于过切点的半径. 公共点已知,连半径,证垂直
公共点未知,作垂直,证半径连接圆心和切点,得到半径,则半径垂直于切线小结请你谈谈今天有哪些收获?选做题
实践调查:寻找圆与直线的位置
关系在实际生活中的应用.必做题
课本98页练习题1;
课本101页习题5,12.作业谢谢大家!
同课章节目录
