人教版数学九年级上册24.2.3 切线长定理课件
文档属性
| 名称 | 人教版数学九年级上册24.2.3 切线长定理课件 |  | |
| 格式 | zip | ||
| 文件大小 | 693.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-24 19:15:24 | ||
图片预览



文档简介
课件23张PPT。24.2.2 直线和圆的位置关系
第3课时学习重点:切线长定理及应用
学习难点:与切线长定理及应用有关的证明和计算问题
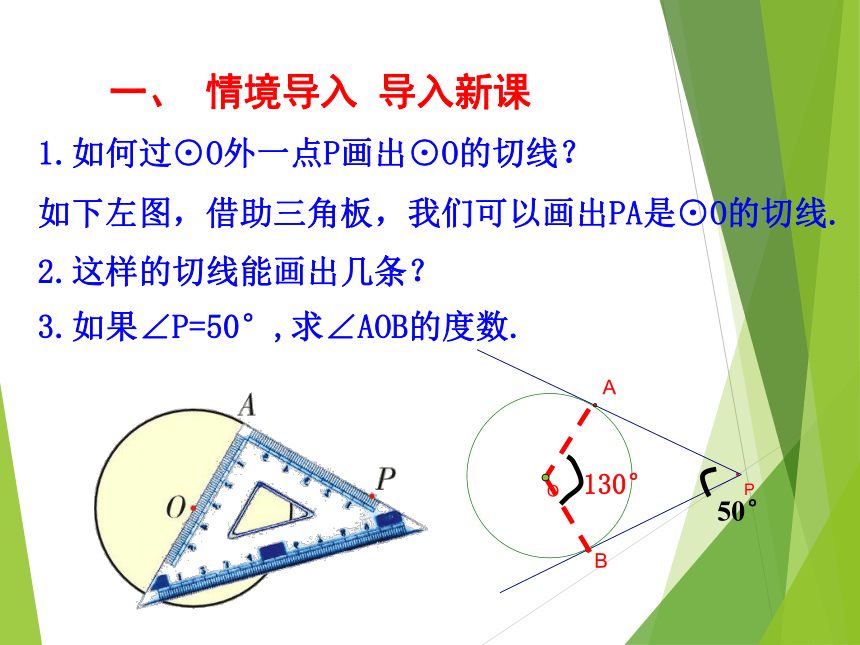
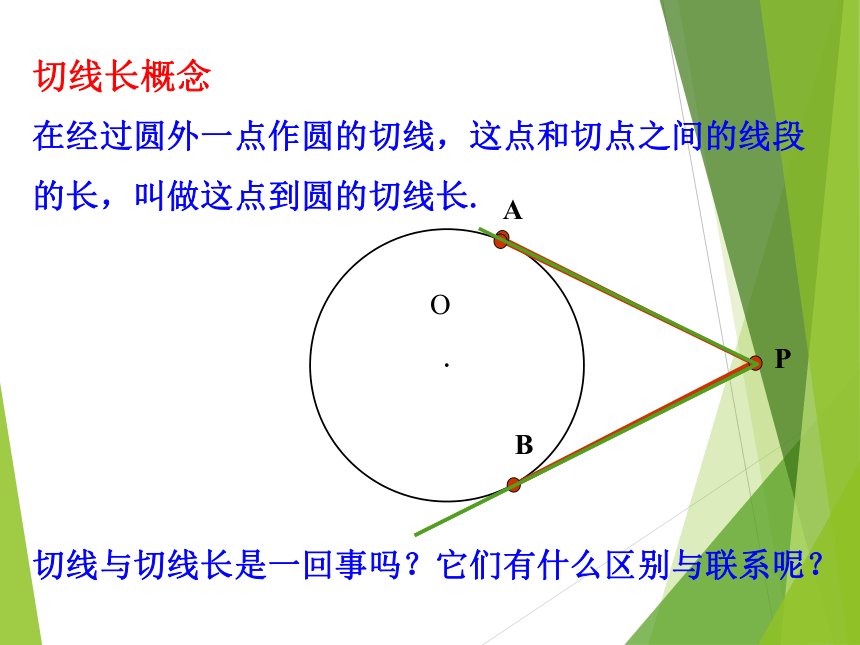
1.如何过⊙O外一点P画出⊙O的切线? 2.这样的切线能画出几条?如下左图,借助三角板,我们可以画出PA是⊙O的切线.3.如果∠P=50°,求∠AOB的度数.50°130°一、 情境导入 导入新课(二)小组合作,探究新知画一画:在白纸上画一个圆,过⊙O外一点P画出⊙O的两条切线,切点分别为A、B在经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.·OPAB切线与切线长是一回事吗?它们有什么区别与联系呢?切线长概念切线和切线长是两个不同的概念:
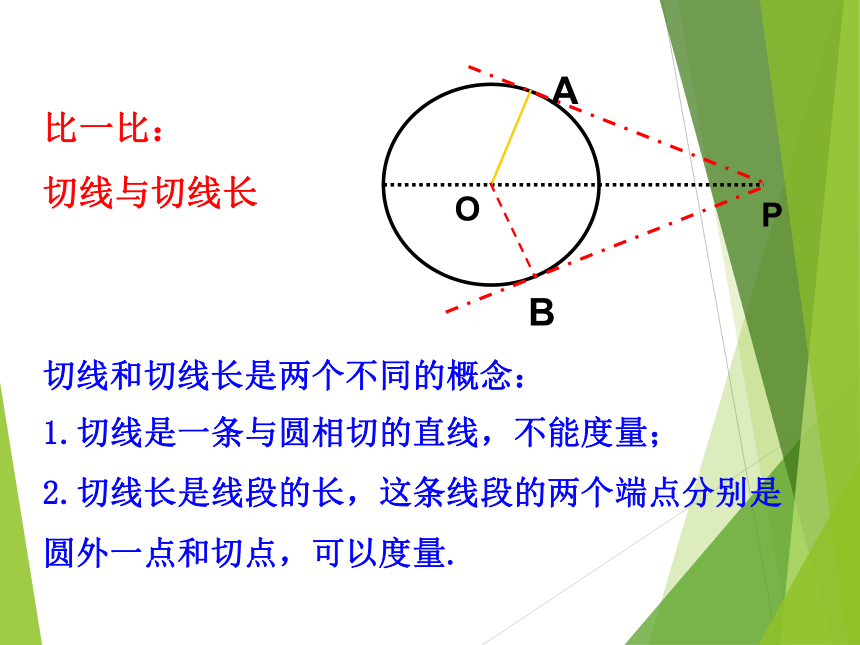
1.切线是一条与圆相切的直线,不能度量;
2.切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.比一比:
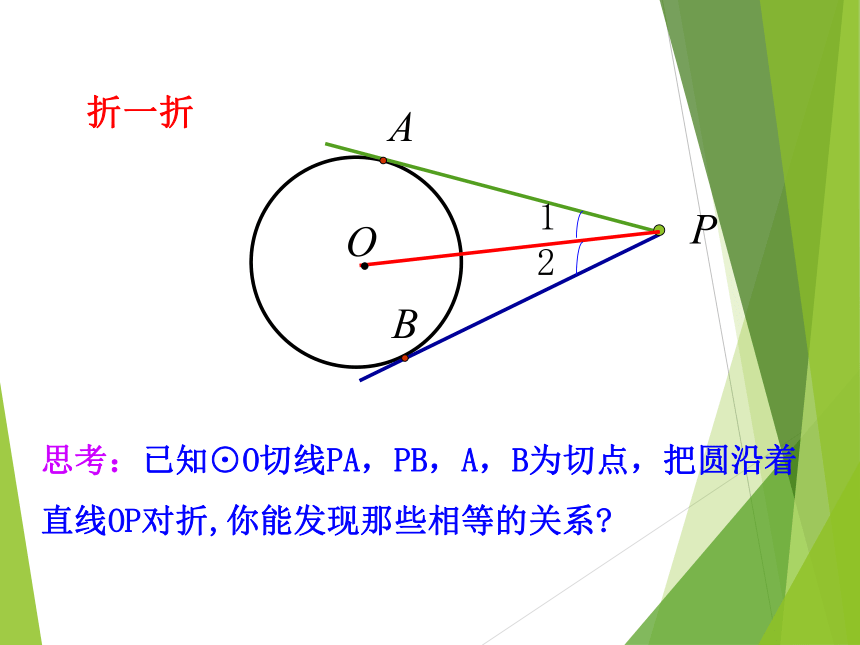
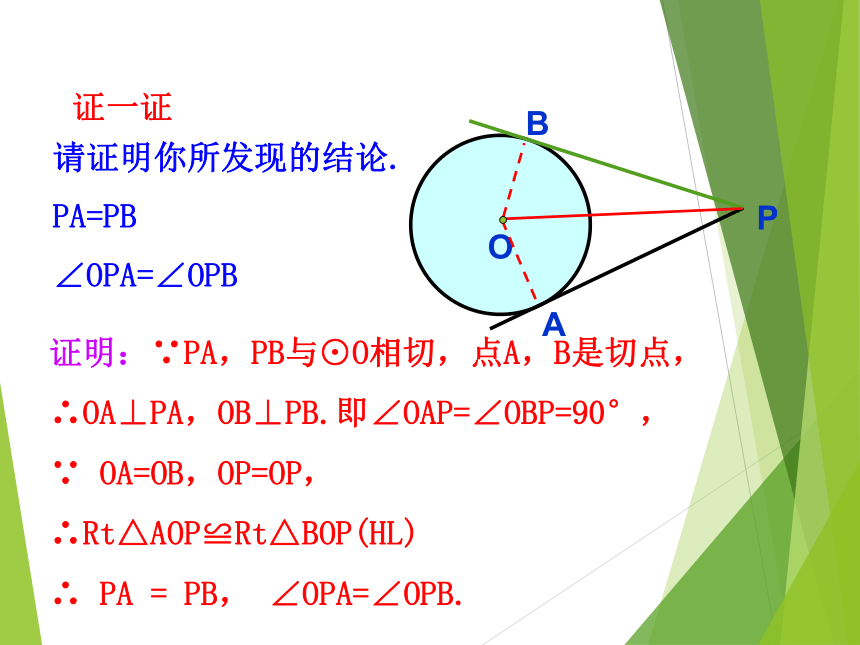
切线与切线长 OABP12思考:已知⊙O切线PA,PB,A,B为切点,把圆沿着直线OP对折,你能发现那些相等的关系?折一折请证明你所发现的结论.PA=PB∠OPA=∠OPB证明:∵PA,PB与⊙O相切,点A,B是切点,
∴OA⊥PA,OB⊥PB.即∠OAP=∠OBP=90°,
∵ OA=OB,OP=OP,
∴Rt△AOP≌Rt△BOP(HL)
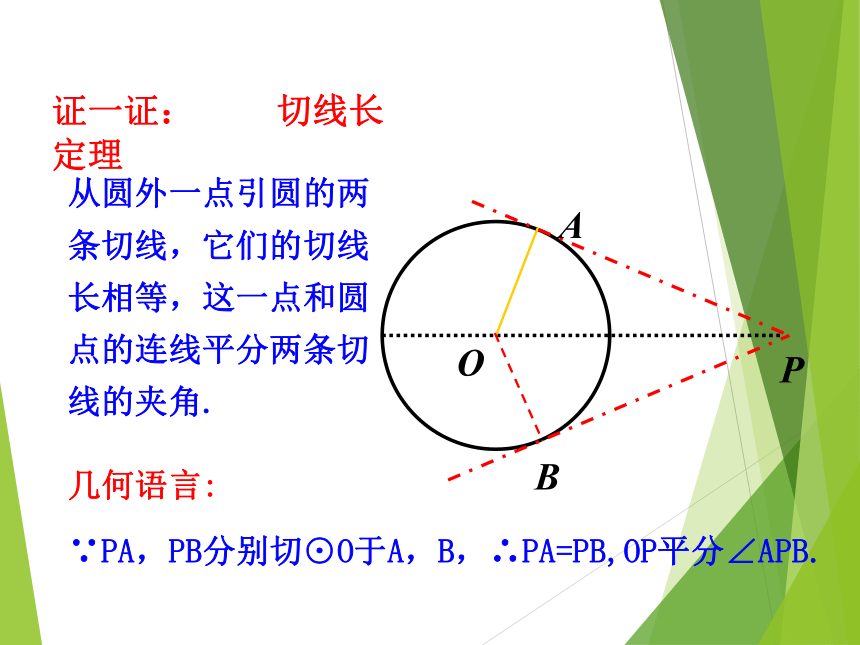
∴ PA = PB, ∠OPA=∠OPB.证一证证一证: 切线长定理∵PA,PB分别切⊙O于A,B,∴PA=PB,OP平分∠APB.从圆外一点引圆的两条切线,它们的切线长相等,这一点和圆点的连线平分两条切线的夹角. 几何语言:反思:切线长定理为证明线段相等、角相等提供新的方法PA =PB∠OPA=∠OPBAPOB1.若连接两切点A,B,AB交OP于点M.你又能得出什么新的结论?并给出证明.OP垂直平分AB证明:∵PA,PB是⊙O的切线,点A,B是切点,
∴PA=PB,∠OPA=∠OPB.
∴△PAB是等腰三角形,PM为顶角的平分线.
∴OP垂直平分AB.试一试APO.B2.若延长PO交⊙O于点C,连接CA,CB,你又能得出什么新的结论?并给出证明.CA=CB证明:∵PA,PB是⊙O的切线,点A,B是切点,
∴PA = PB ,∠OPA=∠OPB.
∴PC=PC.
∴△PCA≌△PCB ,∴AC=BC.C如图,一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使圆的面积尽可能大呢?ID内切圆和内心的定义:与三角形各边都相切的圆叫做三角形的内切圆.
内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.三 应用新知 解决问题.o外接圆圆心:三角形三边垂直平分线的交点。
三角形外接圆三角形内切圆内切圆圆心:三角形三个内角平分线的交点。
AABBCC【例2】△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长.【解析】设AF=x(cm),则AE=x(cm)∴CD=CE=AC-AE=(13-x)cm
BD=BF=AB-AF=(9-x)cm由BD+CD=BC可得
(13-x)+(9-x)=14解得x=4∴ AF=4(cm), BD=5(cm), CE=9(cm).【例题】1.如图所示PA,PB分别切圆O于A,B,并与圆O的切线分别相交于C,D,已知PA=7cm,
(1)求△PCD的周长.
(2)如果∠P=46°,求∠COD的度数. C · OPBDAE答案:14cm 67°四 跟踪训练ABCDEF2.设△ABC的边BC=8,AC=11,AB=15,内切圆I和BC,AC,AB分别相切于点D,E,F.
求AE,CD,BF的长..I 3.如图如果PA,PB是⊙O的两条切线,A,B为切点,PA=4cm,PD=2cm,求半径OA的长.42x
本节课你学到了那些知识?你有什么收获?五、课堂小结1.(珠海·中考)如图,PA,PB是⊙ O的切线,
切点分别是A,B,如果∠P=60°,那么∠AOB等
于( ) A.60° B.90°
C.120° D.150°C六、颗粒归仓 当堂检测 2.如图,正三角形的内切圆半径为1,
那么这个正三角形的边长为( )
A.2 B.3 C. D. 3.已知:如图,PA,PB是⊙O的切线,切点分别是A,B,Q为⊙O上一点,过Q点作⊙O的切线,交PA,PB于E,F点,已知PA=12cm,求△PEF的周长.【解析】易证EQ=EA, FQ=FB,PA=PB.∴ PE+EQ=PA=12cmPF+FQ=PB=PA=12cm∴周长为24cm七、家庭作业1、必做 第100 页题 1、2、第101页6题
2、选做 第102页12题103页14题
第3课时学习重点:切线长定理及应用
学习难点:与切线长定理及应用有关的证明和计算问题
1.如何过⊙O外一点P画出⊙O的切线? 2.这样的切线能画出几条?如下左图,借助三角板,我们可以画出PA是⊙O的切线.3.如果∠P=50°,求∠AOB的度数.50°130°一、 情境导入 导入新课(二)小组合作,探究新知画一画:在白纸上画一个圆,过⊙O外一点P画出⊙O的两条切线,切点分别为A、B在经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.·OPAB切线与切线长是一回事吗?它们有什么区别与联系呢?切线长概念切线和切线长是两个不同的概念:
1.切线是一条与圆相切的直线,不能度量;
2.切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.比一比:
切线与切线长 OABP12思考:已知⊙O切线PA,PB,A,B为切点,把圆沿着直线OP对折,你能发现那些相等的关系?折一折请证明你所发现的结论.PA=PB∠OPA=∠OPB证明:∵PA,PB与⊙O相切,点A,B是切点,
∴OA⊥PA,OB⊥PB.即∠OAP=∠OBP=90°,
∵ OA=OB,OP=OP,
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB, ∠OPA=∠OPB.证一证证一证: 切线长定理∵PA,PB分别切⊙O于A,B,∴PA=PB,OP平分∠APB.从圆外一点引圆的两条切线,它们的切线长相等,这一点和圆点的连线平分两条切线的夹角. 几何语言:反思:切线长定理为证明线段相等、角相等提供新的方法PA =PB∠OPA=∠OPBAPOB1.若连接两切点A,B,AB交OP于点M.你又能得出什么新的结论?并给出证明.OP垂直平分AB证明:∵PA,PB是⊙O的切线,点A,B是切点,
∴PA=PB,∠OPA=∠OPB.
∴△PAB是等腰三角形,PM为顶角的平分线.
∴OP垂直平分AB.试一试APO.B2.若延长PO交⊙O于点C,连接CA,CB,你又能得出什么新的结论?并给出证明.CA=CB证明:∵PA,PB是⊙O的切线,点A,B是切点,
∴PA = PB ,∠OPA=∠OPB.
∴PC=PC.
∴△PCA≌△PCB ,∴AC=BC.C如图,一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使圆的面积尽可能大呢?ID内切圆和内心的定义:与三角形各边都相切的圆叫做三角形的内切圆.
内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.三 应用新知 解决问题.o外接圆圆心:三角形三边垂直平分线的交点。
三角形外接圆三角形内切圆内切圆圆心:三角形三个内角平分线的交点。
AABBCC【例2】△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长.【解析】设AF=x(cm),则AE=x(cm)∴CD=CE=AC-AE=(13-x)cm
BD=BF=AB-AF=(9-x)cm由BD+CD=BC可得
(13-x)+(9-x)=14解得x=4∴ AF=4(cm), BD=5(cm), CE=9(cm).【例题】1.如图所示PA,PB分别切圆O于A,B,并与圆O的切线分别相交于C,D,已知PA=7cm,
(1)求△PCD的周长.
(2)如果∠P=46°,求∠COD的度数. C · OPBDAE答案:14cm 67°四 跟踪训练ABCDEF2.设△ABC的边BC=8,AC=11,AB=15,内切圆I和BC,AC,AB分别相切于点D,E,F.
求AE,CD,BF的长..I 3.如图如果PA,PB是⊙O的两条切线,A,B为切点,PA=4cm,PD=2cm,求半径OA的长.42x
本节课你学到了那些知识?你有什么收获?五、课堂小结1.(珠海·中考)如图,PA,PB是⊙ O的切线,
切点分别是A,B,如果∠P=60°,那么∠AOB等
于( ) A.60° B.90°
C.120° D.150°C六、颗粒归仓 当堂检测 2.如图,正三角形的内切圆半径为1,
那么这个正三角形的边长为( )
A.2 B.3 C. D. 3.已知:如图,PA,PB是⊙O的切线,切点分别是A,B,Q为⊙O上一点,过Q点作⊙O的切线,交PA,PB于E,F点,已知PA=12cm,求△PEF的周长.【解析】易证EQ=EA, FQ=FB,PA=PB.∴ PE+EQ=PA=12cmPF+FQ=PB=PA=12cm∴周长为24cm七、家庭作业1、必做 第100 页题 1、2、第101页6题
2、选做 第102页12题103页14题
同课章节目录
