2017届必考3-5动量新课课件 16.4碰撞 (共24张PPT)
文档属性
| 名称 | 2017届必考3-5动量新课课件 16.4碰撞 (共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2016-11-25 12:58:02 | ||
图片预览







文档简介
课件24张PPT。§ 4 碰 撞1.了解弹性碰撞、非弹性碰撞和完全非弹性碰撞。
2.了解对心碰撞和非对心碰撞。
3.了解散射现象和中子的发现过程,体会理论对实践的指导作用,进一步理解动量守恒定律的普适性。
4.会应用动量和能量的观点综合分析、解决一维碰撞问题。
通过视频慢镜头展示非弹性碰撞和完全非弹性碰撞的过程,使同学们能够感受到碰撞过程物体间的相互作用。进而引入弹性碰撞和非弹性碰撞,导入新课。
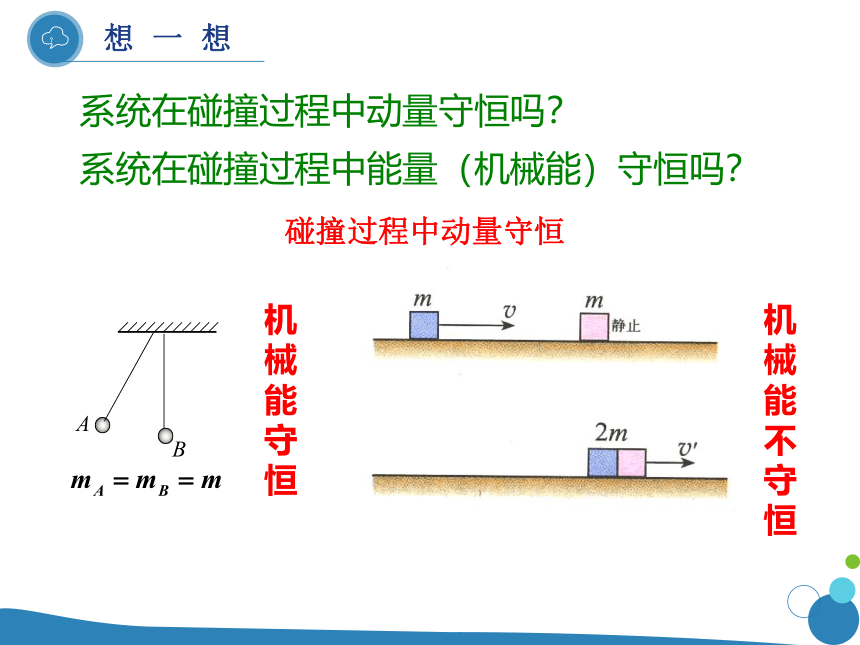
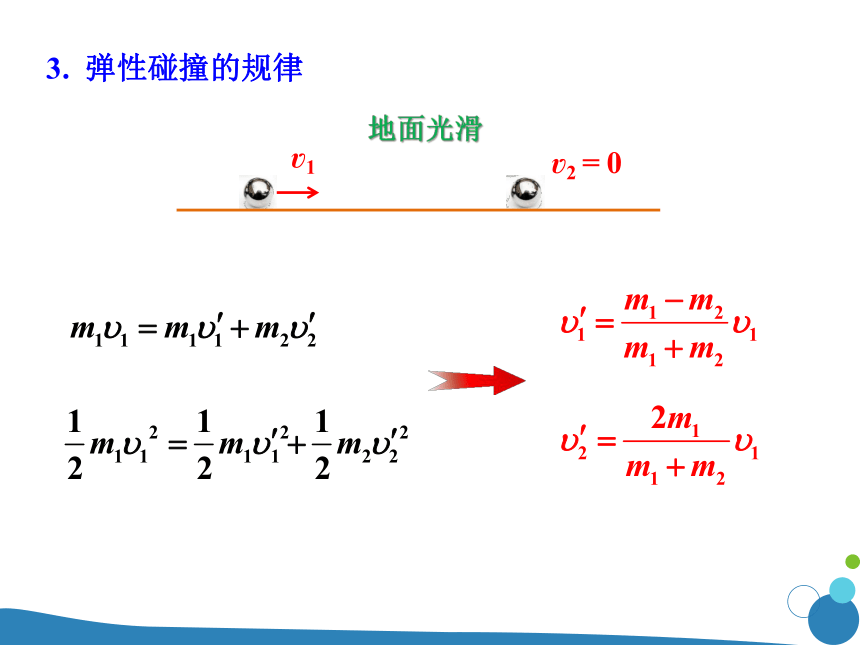
根据不同碰撞形式的能量转化形式,探究了碰撞的规律,使学生对不同碰撞形式问题的处理方法有一个起码的认识。典例探究1使学生清楚碰撞所遵循的基本规律。碰撞是动量守恒定律的一个重要应用。不同的碰撞形式,能量转化不同,与能量结合,可以引申出很多类型的题目。碰撞是动量守恒定律的重要题型,也是高考必考的内容,经常出现在高考和各类模拟试题中。所以本节课在典型例题和课堂检测习题的选择,在学生前两年物理学习能力提高的基础上,难度高于课本,做到一步到位。特别在和其他运动过程的结合上,设计了在实际做题过程中常见的几种情况,如典例探究2和课堂检测4,训练学生对综合题目的分析解决能力。这些问题难度设置的提高,更具有实战意义。非弹性碰撞、完全非弹性碰撞系统在碰撞过程中动量守恒吗?系统在碰撞过程中能量(机械能)守恒吗?机械能守恒机械能不守恒碰撞过程中动量守恒一、弹性碰撞和非弹性碰撞1. 弹性碰撞:如果碰撞过程中机械能守恒,这样的碰撞叫做弹性碰撞。例如钢球、玻璃球的碰撞2. 非弹性碰撞:如果碰撞过程中机械能不守恒,这样的碰撞叫做非弹性碰撞。例如木制品、橡皮泥球的碰撞说明:碰撞后两物体连在一起运动,这类碰撞叫完全非弹性碰撞。此类碰撞是非弹性碰撞中的一种特殊形式,系统机械能损失最多。例如橡皮泥球之间的碰撞3. 弹性碰撞的规律 若 m1 = m2,则 ?1? = 0、?2? = ?1,相当于两球交换速度(5) 若 m1 >> m2 , 则 ?1? = v1, ?2? = 2?1 (2) 若 m1 > m2, 则 ?1? > 0,且 ?2?一定大于 0(3) 若 m1 < m2 , 则 ?1? < 0,且 ?2?一定大于 0?4. 非弹性碰撞5. 完全非弹性碰撞?A1. 动量守恒;
2. 动能不会增加;
3. 符合实际情况。如运动方向一致时,碰撞后,后边物体的速度不大于前边物体的速度。或者碰撞后两物体向相反的方向运动,只能是背道而驰,绝不可以对头“顶牛”。判断碰撞过程能否发生的依据例2 如图所示,光滑的水平地面上有一木板,其左端放有一重物,右方有一竖直的墙。重物质量为木板质量的 2 倍,重物与木板间的动摩擦因数为 μ。使木板与重物以共同的速度 ?0 向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短。求木板从第一次与墙碰撞到再次碰撞所经历的时间。设木板足够长,重物始终在木板上。重力加速度为 g。二、对心碰撞和非对心碰撞1. 对心碰撞 如图所示,一个运动的球与一个静止的球碰撞,碰撞之前球的运动速度与两球心在同一直线上,碰撞之后两球的速度仍会沿着这条直线。这种碰撞称为正碰,也叫对心碰撞。2. 非对心碰撞 一个运动的球与一个静止的球碰撞,碰撞之前球的运动速度与两球心的连线不在同一条直线上,碰撞之后两球的速度都会偏离原来两球心的连线。这种碰撞称为非对心碰撞。斜碰视频三、散 射 与宏观物体碰撞不同的是,微观粒子相互接近时并不发生直接碰撞,因此微观粒子的碰撞又叫做散射。由于粒子与物质微粒发生对心碰撞的概率很小,所以多数粒子在碰撞后飞向四面八方。?1. 弹性碰撞:碰撞过程中机械能守恒,这样的碰撞叫做弹性碰撞。
(1) 规律:动量守恒、机械能守恒
(2) 能量转化情况:系统动能没有损失
2. 非弹性碰撞:碰撞过程中机械能不守恒,这样的碰撞叫做非弹性碰撞。
(1) 规律:动量守恒,机械能减少
(2) 能量转化情况:完全非弹性碰撞中系统动能损失最大
3. 对心碰撞和非对心碰撞1. 在光滑水平面上,动能为 E0 ,动量大小为 p0 的小钢球 1 与静止的小钢球 2 发生碰撞,碰撞前后球 1 的运动方向相反,将碰后球 1 的动能和动量大小分别记为 E1、p1,球 2 的动能和动量大小分别记为 E2、p2,则必有 ( )
A. E1 < E0 B. p1 < p0
C. E2 > E0 D. p2 > p0D2. 如图所示的装置中,木块 B 与水平面间接触是光的,子弹 A 沿水平方向射入木块后留在木块内,将弹簧压缩到最短。现将子弹、木块和弹簧合在一起作为研究对象 (系统),则此系统在从子弹开始射入木块到弹簧压缩至最短的整个过程中 ( )
A. 动量守恒,机械能守恒
B. 动量不守恒,机械能不守恒
C. 动量守恒,机械能不守恒
D. 动量不守恒,机械能守恒BAC4. 如图所示,abc 是光滑的轨道,其中 ab 是水平的,bc 为与 ab 相切的位于竖直平面内的半圆,半径 R = 0.30 m。质量 m = 0.20 kg 的小球 A 静止在轨道上,另一质量 M = 0.60 kg、速度 v0 = 5.5 m/s 的小球 B 与小球 A 正碰。已知相碰后小球 A 经过半圆的最高点 c 落到轨道上距 b 点为 处,重力加速度 g 取 10 m/s2,求碰撞结束时,小球 A 和 B的速度的大小。vA = 6 m/svB = 3.5 m/s
2.了解对心碰撞和非对心碰撞。
3.了解散射现象和中子的发现过程,体会理论对实践的指导作用,进一步理解动量守恒定律的普适性。
4.会应用动量和能量的观点综合分析、解决一维碰撞问题。
通过视频慢镜头展示非弹性碰撞和完全非弹性碰撞的过程,使同学们能够感受到碰撞过程物体间的相互作用。进而引入弹性碰撞和非弹性碰撞,导入新课。
根据不同碰撞形式的能量转化形式,探究了碰撞的规律,使学生对不同碰撞形式问题的处理方法有一个起码的认识。典例探究1使学生清楚碰撞所遵循的基本规律。碰撞是动量守恒定律的一个重要应用。不同的碰撞形式,能量转化不同,与能量结合,可以引申出很多类型的题目。碰撞是动量守恒定律的重要题型,也是高考必考的内容,经常出现在高考和各类模拟试题中。所以本节课在典型例题和课堂检测习题的选择,在学生前两年物理学习能力提高的基础上,难度高于课本,做到一步到位。特别在和其他运动过程的结合上,设计了在实际做题过程中常见的几种情况,如典例探究2和课堂检测4,训练学生对综合题目的分析解决能力。这些问题难度设置的提高,更具有实战意义。非弹性碰撞、完全非弹性碰撞系统在碰撞过程中动量守恒吗?系统在碰撞过程中能量(机械能)守恒吗?机械能守恒机械能不守恒碰撞过程中动量守恒一、弹性碰撞和非弹性碰撞1. 弹性碰撞:如果碰撞过程中机械能守恒,这样的碰撞叫做弹性碰撞。例如钢球、玻璃球的碰撞2. 非弹性碰撞:如果碰撞过程中机械能不守恒,这样的碰撞叫做非弹性碰撞。例如木制品、橡皮泥球的碰撞说明:碰撞后两物体连在一起运动,这类碰撞叫完全非弹性碰撞。此类碰撞是非弹性碰撞中的一种特殊形式,系统机械能损失最多。例如橡皮泥球之间的碰撞3. 弹性碰撞的规律 若 m1 = m2,则 ?1? = 0、?2? = ?1,相当于两球交换速度(5) 若 m1 >> m2 , 则 ?1? = v1, ?2? = 2?1 (2) 若 m1 > m2, 则 ?1? > 0,且 ?2?一定大于 0(3) 若 m1 < m2 , 则 ?1? < 0,且 ?2?一定大于 0?4. 非弹性碰撞5. 完全非弹性碰撞?A1. 动量守恒;
2. 动能不会增加;
3. 符合实际情况。如运动方向一致时,碰撞后,后边物体的速度不大于前边物体的速度。或者碰撞后两物体向相反的方向运动,只能是背道而驰,绝不可以对头“顶牛”。判断碰撞过程能否发生的依据例2 如图所示,光滑的水平地面上有一木板,其左端放有一重物,右方有一竖直的墙。重物质量为木板质量的 2 倍,重物与木板间的动摩擦因数为 μ。使木板与重物以共同的速度 ?0 向右运动,某时刻木板与墙发生弹性碰撞,碰撞时间极短。求木板从第一次与墙碰撞到再次碰撞所经历的时间。设木板足够长,重物始终在木板上。重力加速度为 g。二、对心碰撞和非对心碰撞1. 对心碰撞 如图所示,一个运动的球与一个静止的球碰撞,碰撞之前球的运动速度与两球心在同一直线上,碰撞之后两球的速度仍会沿着这条直线。这种碰撞称为正碰,也叫对心碰撞。2. 非对心碰撞 一个运动的球与一个静止的球碰撞,碰撞之前球的运动速度与两球心的连线不在同一条直线上,碰撞之后两球的速度都会偏离原来两球心的连线。这种碰撞称为非对心碰撞。斜碰视频三、散 射 与宏观物体碰撞不同的是,微观粒子相互接近时并不发生直接碰撞,因此微观粒子的碰撞又叫做散射。由于粒子与物质微粒发生对心碰撞的概率很小,所以多数粒子在碰撞后飞向四面八方。?1. 弹性碰撞:碰撞过程中机械能守恒,这样的碰撞叫做弹性碰撞。
(1) 规律:动量守恒、机械能守恒
(2) 能量转化情况:系统动能没有损失
2. 非弹性碰撞:碰撞过程中机械能不守恒,这样的碰撞叫做非弹性碰撞。
(1) 规律:动量守恒,机械能减少
(2) 能量转化情况:完全非弹性碰撞中系统动能损失最大
3. 对心碰撞和非对心碰撞1. 在光滑水平面上,动能为 E0 ,动量大小为 p0 的小钢球 1 与静止的小钢球 2 发生碰撞,碰撞前后球 1 的运动方向相反,将碰后球 1 的动能和动量大小分别记为 E1、p1,球 2 的动能和动量大小分别记为 E2、p2,则必有 ( )
A. E1 < E0 B. p1 < p0
C. E2 > E0 D. p2 > p0D2. 如图所示的装置中,木块 B 与水平面间接触是光的,子弹 A 沿水平方向射入木块后留在木块内,将弹簧压缩到最短。现将子弹、木块和弹簧合在一起作为研究对象 (系统),则此系统在从子弹开始射入木块到弹簧压缩至最短的整个过程中 ( )
A. 动量守恒,机械能守恒
B. 动量不守恒,机械能不守恒
C. 动量守恒,机械能不守恒
D. 动量不守恒,机械能守恒BAC4. 如图所示,abc 是光滑的轨道,其中 ab 是水平的,bc 为与 ab 相切的位于竖直平面内的半圆,半径 R = 0.30 m。质量 m = 0.20 kg 的小球 A 静止在轨道上,另一质量 M = 0.60 kg、速度 v0 = 5.5 m/s 的小球 B 与小球 A 正碰。已知相碰后小球 A 经过半圆的最高点 c 落到轨道上距 b 点为 处,重力加速度 g 取 10 m/s2,求碰撞结束时,小球 A 和 B的速度的大小。vA = 6 m/svB = 3.5 m/s
