鲁教版八年级数学上册第四章旋转和中心对称练习题
文档属性
| 名称 | 鲁教版八年级数学上册第四章旋转和中心对称练习题 |
|
|
| 格式 | zip | ||
| 文件大小 | 221.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-25 00:00:00 | ||
图片预览

文档简介
鲁教版八年级数学上册第四单元旋转和中心对称练习题
一.选择题(共13小题)
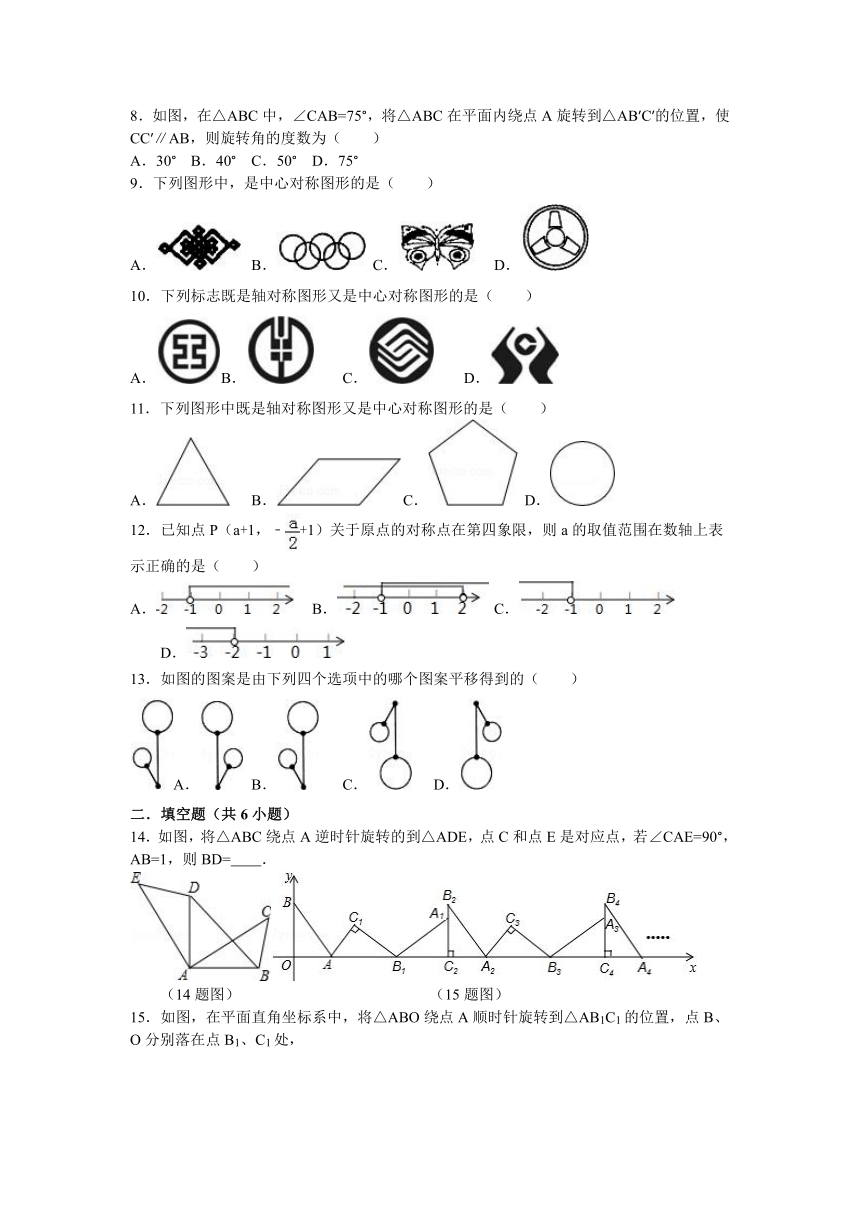
1.如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是( )
A.60°
B.90°
C.120°
D.150°
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(1题图)
(2题图)
(3题图)
2.如图,在Rt△ABC中,∠BAC=9
( http: / / www.21cnjy.com )0°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,点A在边B′C上,则∠B′的大小为( )
A.42°
B.48°
C.52°
D.58°
3.如图,在三角形ABC中,∠ACB=90
( http: / / www.21cnjy.com )°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC、A′B′交于点O,则∠COA′的度数是( )
A.50°
B.60°
C.70°
D.80°
4.如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )
A.(2,5)
B.(5,2)
C.(2,﹣5)
D.(5,﹣2)
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(4题图)
(5题图)
(7题图)
(8题图)
5.将含有30°角的直角三角板OAB如图放
( http: / / www.21cnjy.com )置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )
A.(,﹣1)
B.(1,﹣)
C.(,﹣)
D.(﹣,)
6.如图,在正方形网格中有△ABC,△ABC绕O点按逆时针旋转90°后的图案应该是( )
A.
( http: / / www.21cnjy.com )
B.
( http: / / www.21cnjy.com )
C.
( http: / / www.21cnjy.com )
D.
( http: / / www.21cnjy.com )
7.如图,△ABC为等腰直
( http: / / www.21cnjy.com )角三角形,∠ACB=90°,将△ABC绕点
A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )
A.2
B.3
C.2
D.3
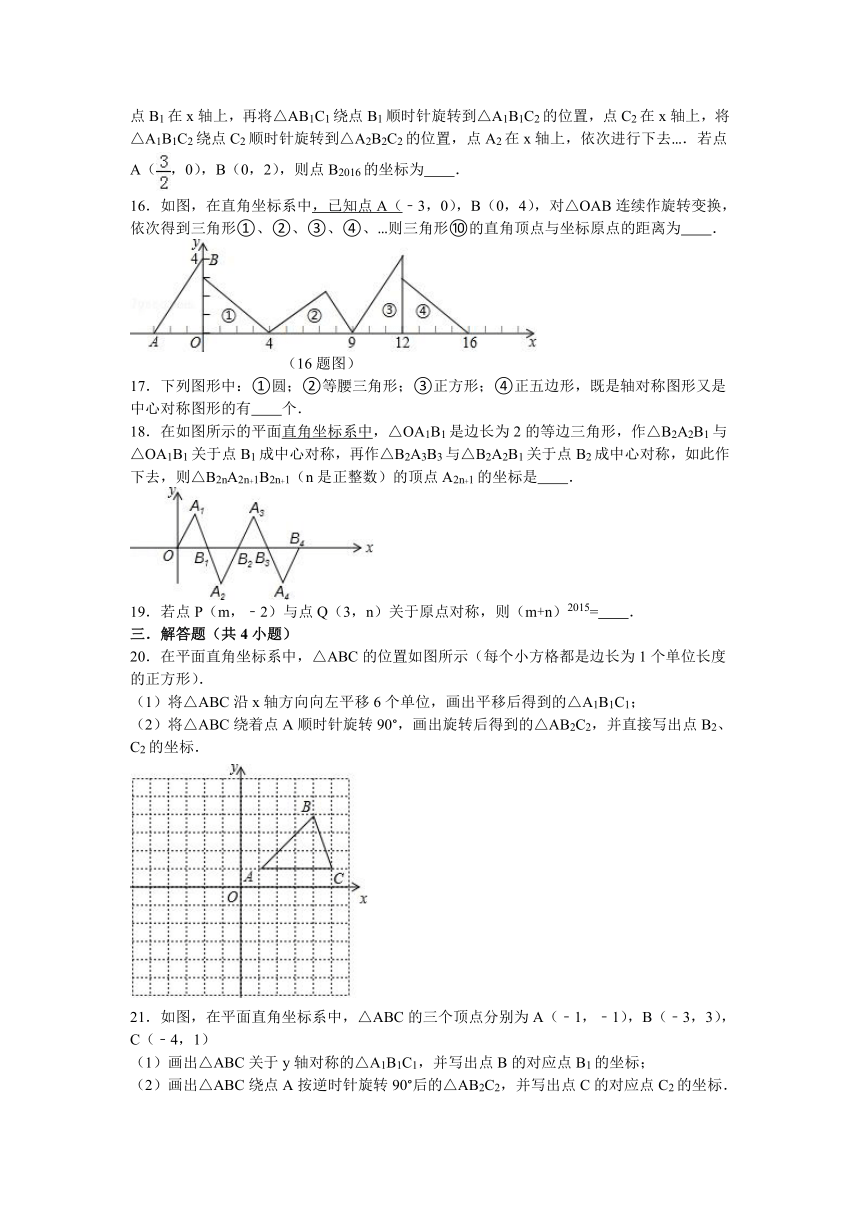
8.如图,在△ABC中,∠CAB=75°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
A.30°
B.40°
C.50°
D.75°
9.下列图形中,是中心对称图形的是( )
A.
B.
C.
D.
10.下列标志既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
11.下列图形中既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
( http: / / www.21cnjy.com )
D.
12.已知点P(a+1,﹣+1)关于原点的对称点在第四象限,则a的取值范围在数轴上表示正确的是( )
A.
B.
C.
D.
13.如图的图案是由下列四个选项中的哪个图案平移得到的( )
A.
B.
C.
D.
二.填空题(共6小题)
14.如图,将△ABC绕点A逆时针旋转的到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则BD= .
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(14题图)
(15题图)
15.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,
点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,2),则点B2016的坐标为 .
16.如图,在直角坐标系中,已知点A(
( http: / / www.21cnjy.com )﹣3,0),B(0,4),对△OAB连续作旋转变换,依次得到三角形①、②、③、④、…则三角形⑩的直角顶点与坐标原点的距离为 .
( http: / / www.21cnjy.com )
(16题图)
17.下列图形中:①圆;②等腰三角形;③正方形;④正五边形,既是轴对称图形又是中心对称图形的有 个.
18.在如图所示的平面直角坐标系中
( http: / / www.21cnjy.com ),△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是 .
( http: / / www.21cnjy.com )
19.若点P(m,﹣2)与点Q(3,n)关于原点对称,则(m+n)2015= .
三.解答题(共4小题)
20.在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.
( http: / / www.21cnjy.com )
21.如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣1),B(﹣3,3),C(﹣4,1)
(1)画出△ABC关于y轴对称的△A1B1C1,并写出点B的对应点B1的坐标;
(2)画出△ABC绕点A按逆时针旋转90°后的△AB2C2,并写出点C的对应点C2的坐标.
( http: / / www.21cnjy.com )
22.如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.线段CD绕点C顺时针旋转60°得到线段CE,连接AE.
(1)求证:AE=BD;
(2)若∠ADC=30°,AD=3,BD=4.求CD的长.
( http: / / www.21cnjy.com )
23.如图,△ABC与△A′B′C′关于某一个点成中心对称,点A,B的对称点分别为点A′和B′.请找出对称中心O,并把图形补充完整.
( http: / / www.21cnjy.com )
参考答案与试题解析
一.选择题(共13小题)
1、D.2.A.3.
B.4.B.5.C.6.
A.7.
D.8.A.9.A.10.A.
11.D.12.C.13.
B.
二.填空题(共6小题)
14. .
15.(6048,2) .
【解答】解:∵AO=,BO=2,∴AB==,∴OA+AB1+B1C2=6,
∴B2的横坐标为:6,且B2C2=2,∴B4的横坐标为:2×6=12,
∴点B2016的横坐标为:2016÷2×6=6048.
∴点B2016的纵坐标为:2.∴点B2016的坐标为:(6048,2).
故答案为:(6048,2).
16. 36 .
解:∵A(﹣3,0),B(0,4),∴OA=3,OB=4,∴AB==5,
∵对△OAB连续作如图所示的旋转变换,
∴△OAB每三次旋转后回到原来的状态,并且每三次向前移动了3+4+5=12个单位,
∵10=3×3+1,
∴三角形⑩和三角形①的状态一样,则三角形⑩与三角形⑨的直角顶点相同,
∴三角形⑩的直角顶点的横坐标为3×12=36,纵坐标为0,
∴三角形⑩的直角顶点与坐标原点的距离为36.
故答案为36.
17. ①③ 个.18.(4n+1,) .
解:∵△OA1B1是边长为2的等边三角形,
∴A1的坐标为(1,),B1的坐标为(2,0),
∵△B2A2B1与△OA1B1关于点B1成中心对称,
∴点A2与点A1关于点B1成中心对称,
∵2×2﹣1=3,2×0﹣=﹣,
∴点A2的坐标是(3,﹣),
∵△B2A3B3与△B2A2B1关于点B2成中心对称,
∴点A3与点A2关于点B2成中心对称,
∵2×4﹣3=5,2×0﹣(﹣)=,
∴点A3的坐标是(5,),
∵△B3A4B4与△B3A3B2关于点B3成中心对称,
∴点A4与点A3关于点B3成中心对称,
∵2×6﹣5=7,2×0﹣=﹣,
∴点A4的坐标是(7,﹣),
…,
∵1=2×1﹣1,3=2×2﹣1,5=2×3﹣1,7=2×3﹣1,…,
∴An的横坐标是2n﹣1,A2n+1的横坐标是2(2n+1)﹣1=4n+1,
∵当n为奇数时,An的纵坐标是,当n为偶数时,An的纵坐标是﹣,
∴顶点A2n+1的纵坐标是,
∴△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是(4n+1,).
故答案为:(4n+1,).
19. ﹣1 .
三.解答题(共4小题)
20.解:(1)如图,△A1B1C1即为所求;
(2)如图,△AB2C2即为所求,点B2(4,﹣2),C2(1,﹣3).
( http: / / www.21cnjy.com )
21.解:(1)如图所示,△A1B1C1即为△ABC关于y轴对称的图形;
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
则B1的坐标是(3,3);
(2)△ABC绕点A按逆时针旋转90°后的△AB2C2是:
则点C的对应点C2的坐标是(1,2).
22.解:(1)∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°.
由旋转的性质可得:
CE=CD,∠DCE=60°.
∴∠DCE+∠ACD=∠ACB+∠ACD,
即∠ACE=∠BCD.
在△ACE≌△BCD中,∵,∴△ACE≌△BCD.∴AE=BD.
(2)连接DE.
( http: / / www.21cnjy.com )
∵CD=CE,∠DCE=60°,∴△DCE是等边三角形.∴∠CDE=60°,DC=DE.
∵∠ADC=30°,∴∠ADC+∠CDE=90°.
∵AD=3,BD=4,∴AE=BD=4.
在Rt△ADE中,由勾股定理,可得DE===.
∴DC=DE=.
23.解:作法:
①连接BB′和AA′,交于点O,则点O就是对称中心,
②连接CO并延长至C′,使CO=C′O,
③连接A′B′、B′C′、A′C′,则△A’B’C′就是对称三角形.
( http: / / www.21cnjy.com )
一.选择题(共13小题)
1.如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是( )
A.60°
B.90°
C.120°
D.150°
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(1题图)
(2题图)
(3题图)
2.如图,在Rt△ABC中,∠BAC=9
( http: / / www.21cnjy.com )0°,将Rt△ABC绕点C按逆时针方向旋转48°得到Rt△A′B′C′,点A在边B′C上,则∠B′的大小为( )
A.42°
B.48°
C.52°
D.58°
3.如图,在三角形ABC中,∠ACB=90
( http: / / www.21cnjy.com )°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC、A′B′交于点O,则∠COA′的度数是( )
A.50°
B.60°
C.70°
D.80°
4.如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是( )
A.(2,5)
B.(5,2)
C.(2,﹣5)
D.(5,﹣2)
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(4题图)
(5题图)
(7题图)
(8题图)
5.将含有30°角的直角三角板OAB如图放
( http: / / www.21cnjy.com )置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )
A.(,﹣1)
B.(1,﹣)
C.(,﹣)
D.(﹣,)
6.如图,在正方形网格中有△ABC,△ABC绕O点按逆时针旋转90°后的图案应该是( )
A.
( http: / / www.21cnjy.com )
B.
( http: / / www.21cnjy.com )
C.
( http: / / www.21cnjy.com )
D.
( http: / / www.21cnjy.com )
7.如图,△ABC为等腰直
( http: / / www.21cnjy.com )角三角形,∠ACB=90°,将△ABC绕点
A逆时针旋转75°,得到△AB′C′,过点B′作B′D⊥CA,交CA的延长线于点D,若AC=6,则AD的长为( )
A.2
B.3
C.2
D.3
8.如图,在△ABC中,∠CAB=75°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
A.30°
B.40°
C.50°
D.75°
9.下列图形中,是中心对称图形的是( )
A.
B.
C.
D.
10.下列标志既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
11.下列图形中既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
( http: / / www.21cnjy.com )
D.
12.已知点P(a+1,﹣+1)关于原点的对称点在第四象限,则a的取值范围在数轴上表示正确的是( )
A.
B.
C.
D.
13.如图的图案是由下列四个选项中的哪个图案平移得到的( )
A.
B.
C.
D.
二.填空题(共6小题)
14.如图,将△ABC绕点A逆时针旋转的到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则BD= .
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(14题图)
(15题图)
15.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,
点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,2),则点B2016的坐标为 .
16.如图,在直角坐标系中,已知点A(
( http: / / www.21cnjy.com )﹣3,0),B(0,4),对△OAB连续作旋转变换,依次得到三角形①、②、③、④、…则三角形⑩的直角顶点与坐标原点的距离为 .
( http: / / www.21cnjy.com )
(16题图)
17.下列图形中:①圆;②等腰三角形;③正方形;④正五边形,既是轴对称图形又是中心对称图形的有 个.
18.在如图所示的平面直角坐标系中
( http: / / www.21cnjy.com ),△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是 .
( http: / / www.21cnjy.com )
19.若点P(m,﹣2)与点Q(3,n)关于原点对称,则(m+n)2015= .
三.解答题(共4小题)
20.在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.
( http: / / www.21cnjy.com )
21.如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣1,﹣1),B(﹣3,3),C(﹣4,1)
(1)画出△ABC关于y轴对称的△A1B1C1,并写出点B的对应点B1的坐标;
(2)画出△ABC绕点A按逆时针旋转90°后的△AB2C2,并写出点C的对应点C2的坐标.
( http: / / www.21cnjy.com )
22.如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.线段CD绕点C顺时针旋转60°得到线段CE,连接AE.
(1)求证:AE=BD;
(2)若∠ADC=30°,AD=3,BD=4.求CD的长.
( http: / / www.21cnjy.com )
23.如图,△ABC与△A′B′C′关于某一个点成中心对称,点A,B的对称点分别为点A′和B′.请找出对称中心O,并把图形补充完整.
( http: / / www.21cnjy.com )
参考答案与试题解析
一.选择题(共13小题)
1、D.2.A.3.
B.4.B.5.C.6.
A.7.
D.8.A.9.A.10.A.
11.D.12.C.13.
B.
二.填空题(共6小题)
14. .
15.(6048,2) .
【解答】解:∵AO=,BO=2,∴AB==,∴OA+AB1+B1C2=6,
∴B2的横坐标为:6,且B2C2=2,∴B4的横坐标为:2×6=12,
∴点B2016的横坐标为:2016÷2×6=6048.
∴点B2016的纵坐标为:2.∴点B2016的坐标为:(6048,2).
故答案为:(6048,2).
16. 36 .
解:∵A(﹣3,0),B(0,4),∴OA=3,OB=4,∴AB==5,
∵对△OAB连续作如图所示的旋转变换,
∴△OAB每三次旋转后回到原来的状态,并且每三次向前移动了3+4+5=12个单位,
∵10=3×3+1,
∴三角形⑩和三角形①的状态一样,则三角形⑩与三角形⑨的直角顶点相同,
∴三角形⑩的直角顶点的横坐标为3×12=36,纵坐标为0,
∴三角形⑩的直角顶点与坐标原点的距离为36.
故答案为36.
17. ①③ 个.18.(4n+1,) .
解:∵△OA1B1是边长为2的等边三角形,
∴A1的坐标为(1,),B1的坐标为(2,0),
∵△B2A2B1与△OA1B1关于点B1成中心对称,
∴点A2与点A1关于点B1成中心对称,
∵2×2﹣1=3,2×0﹣=﹣,
∴点A2的坐标是(3,﹣),
∵△B2A3B3与△B2A2B1关于点B2成中心对称,
∴点A3与点A2关于点B2成中心对称,
∵2×4﹣3=5,2×0﹣(﹣)=,
∴点A3的坐标是(5,),
∵△B3A4B4与△B3A3B2关于点B3成中心对称,
∴点A4与点A3关于点B3成中心对称,
∵2×6﹣5=7,2×0﹣=﹣,
∴点A4的坐标是(7,﹣),
…,
∵1=2×1﹣1,3=2×2﹣1,5=2×3﹣1,7=2×3﹣1,…,
∴An的横坐标是2n﹣1,A2n+1的横坐标是2(2n+1)﹣1=4n+1,
∵当n为奇数时,An的纵坐标是,当n为偶数时,An的纵坐标是﹣,
∴顶点A2n+1的纵坐标是,
∴△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是(4n+1,).
故答案为:(4n+1,).
19. ﹣1 .
三.解答题(共4小题)
20.解:(1)如图,△A1B1C1即为所求;
(2)如图,△AB2C2即为所求,点B2(4,﹣2),C2(1,﹣3).
( http: / / www.21cnjy.com )
21.解:(1)如图所示,△A1B1C1即为△ABC关于y轴对称的图形;
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
则B1的坐标是(3,3);
(2)△ABC绕点A按逆时针旋转90°后的△AB2C2是:
则点C的对应点C2的坐标是(1,2).
22.解:(1)∵△ABC是等边三角形,
∴AC=BC,∠ACB=60°.
由旋转的性质可得:
CE=CD,∠DCE=60°.
∴∠DCE+∠ACD=∠ACB+∠ACD,
即∠ACE=∠BCD.
在△ACE≌△BCD中,∵,∴△ACE≌△BCD.∴AE=BD.
(2)连接DE.
( http: / / www.21cnjy.com )
∵CD=CE,∠DCE=60°,∴△DCE是等边三角形.∴∠CDE=60°,DC=DE.
∵∠ADC=30°,∴∠ADC+∠CDE=90°.
∵AD=3,BD=4,∴AE=BD=4.
在Rt△ADE中,由勾股定理,可得DE===.
∴DC=DE=.
23.解:作法:
①连接BB′和AA′,交于点O,则点O就是对称中心,
②连接CO并延长至C′,使CO=C′O,
③连接A′B′、B′C′、A′C′,则△A’B’C′就是对称三角形.
( http: / / www.21cnjy.com )
