多边形的内角和课件
图片预览






文档简介
课件20张PPT。 《多边形的内角和》课件
课题:新人教版九年义务教育阶段七年级下册第七章
第三节第二课时“多边形的内角和”的教学内容
学校:绥阳县坪乐中学
作者:曾 涛
电话:13765984160多边形的内角和 绥阳县坪乐中学:曾涛
1、从n边形的一个顶点可以引_____对角线
将n边形分成了________个三角形。
2、n边形的对角线一共有______条。
(n-3)(n-2)温故知新3、三角形的内角和等于 ____,外角和等____。180○360○
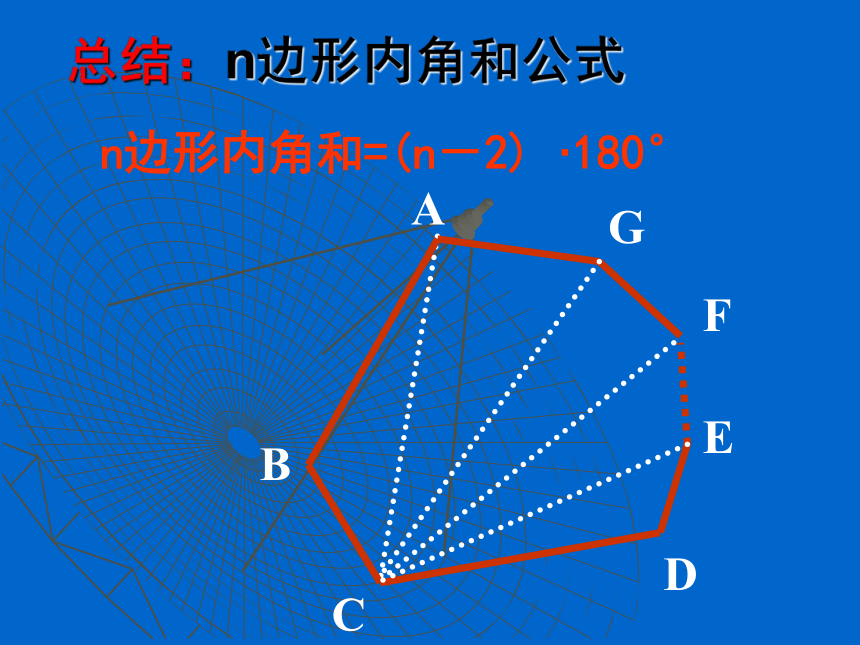
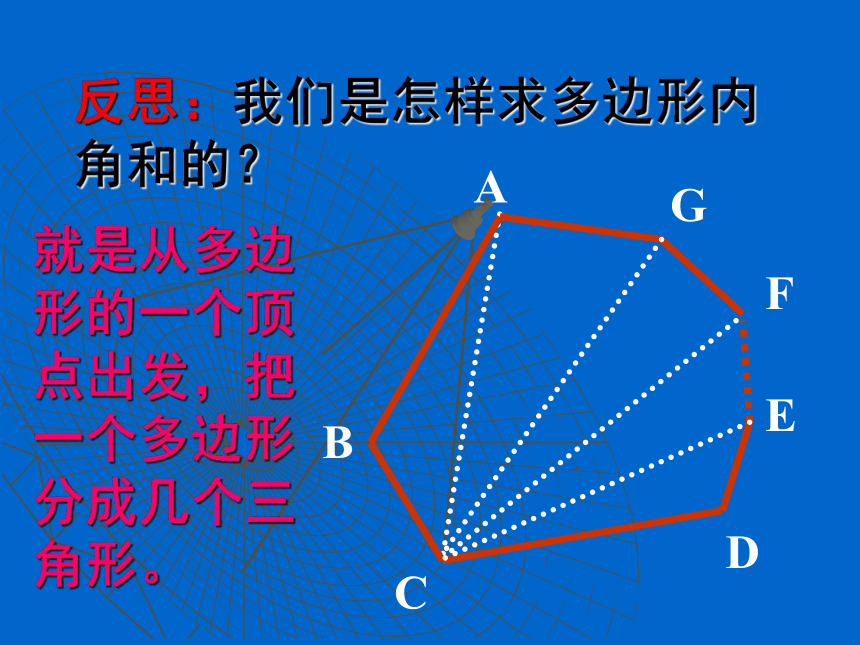
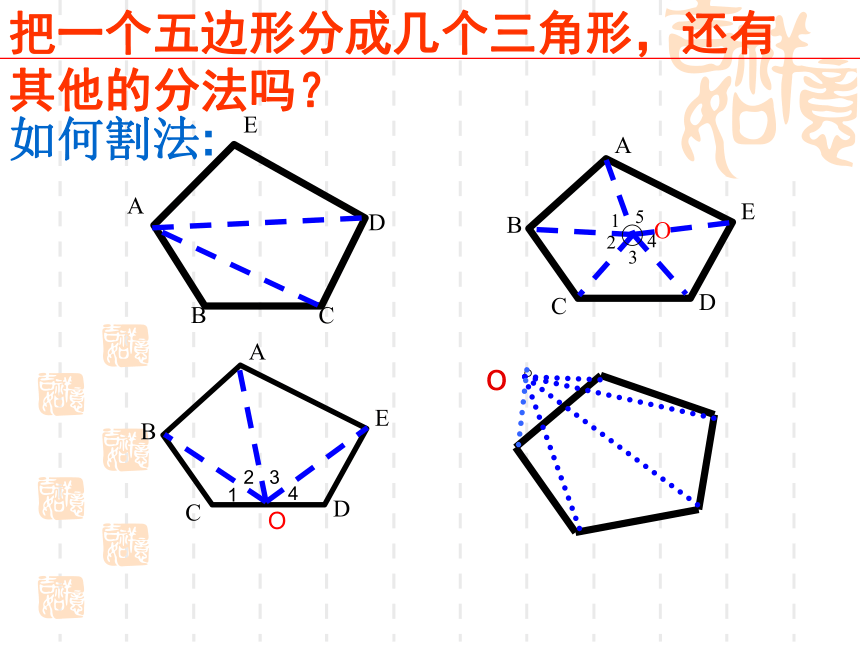
探究:五边形的内角和是多少?六边形、七边形呢?探究:多边形的内角和 任意画一个四边形,量出它的4个内角的度数,并计算它们的和.你还有其他方法得到四边形的内角和吗?………………34567n1n-2235180°360°540°720°900°(n-2) ·180°(n-2) ·180°(4-2)×180°(3-2)×180°(3-2)×180°(4-2)×180°(3-2)×180°4总结:n边形内角和公式n边形内角和=(n-2) ·180°反思:我们是怎样求多边形内 角和的?就是从多边形的一个顶点出发,把一个多边形分成几个三角形。O15432O1234如何割法:o把一个五边形分成几个三角形,还有其他的分法吗?n边形内角和公式的应用n边形内角和=(n-2) ·180°练习:看谁求得又快又准!x°140°∟120°150°2x°x°120°80°75°x°X=65X=60X=95火眼金睛(2)(3)例1:如果一个四边形的一组对角互补, 那么另一组对角有什么关系?解:如图所示,四边形ABCD中,
∠A+∠C= 180°
∵∠A+∠B+ ∠C+ ∠D=(4-2)×180。=360°
∴∠B+∠D = 360° -(∠A+∠C )
= 360° - 180°
= 180°
这就是说,如果四边形的一组对角互补,那么另一组对角也互补。 例2 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
分析:
1.任意一个外角和他相邻的内角有什么关系?
2.五个外角加上他们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系? 6 例2 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
解:5边形外角和 结论:五边形的外角和等于360°
-(5-2) × 180°
=360 ° 6=5个平角-5边形内角和
=5×180°探究 如果将例2中五边形换成n边(n≥3)
可以得到同样的结果吗?n边形外角和=结论:
n边形的外角和等于360°-(n-2) × 180°=360 °n个平角-n边形内角和=n×180 °课堂练习:练一练练习1:如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。12n×30°=360°n=12n边形外角和=360 °练一练练习2:正五边形的每一个外角等于____,每一个内角等于_____。5X=360°X=72°72°144°解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:所以每一个内角度数为108 °练习. 已知一个多边形,它的内角和等于外角和,它是几边形? 解: 设多边形的边数为n
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360o,
∴ (n-2)?180°= 360o。
解得: n=4
∴这个多边形的边数为4。
感悟与反思n边形内角和=(n-2) ·180°n边形外角和=360°n边形外角和= n个平角-n边形内角和 通过这节课的学习你有哪些收获? 作 业
P84习题7.3 的2、6题 再见
1、从n边形的一个顶点可以引_____对角线
将n边形分成了________个三角形。
2、n边形的对角线一共有______条。
(n-3)(n-2)温故知新3、三角形的内角和等于 ____,外角和等____。180○360○
探究:五边形的内角和是多少?六边形、七边形呢?探究:多边形的内角和 任意画一个四边形,量出它的4个内角的度数,并计算它们的和.你还有其他方法得到四边形的内角和吗?………………34567n1n-2235180°360°540°720°900°(n-2) ·180°(n-2) ·180°(4-2)×180°(3-2)×180°(3-2)×180°(4-2)×180°(3-2)×180°4总结:n边形内角和公式n边形内角和=(n-2) ·180°反思:我们是怎样求多边形内 角和的?就是从多边形的一个顶点出发,把一个多边形分成几个三角形。O15432O1234如何割法:o把一个五边形分成几个三角形,还有其他的分法吗?n边形内角和公式的应用n边形内角和=(n-2) ·180°练习:看谁求得又快又准!x°140°∟120°150°2x°x°120°80°75°x°X=65X=60X=95火眼金睛(2)(3)例1:如果一个四边形的一组对角互补, 那么另一组对角有什么关系?解:如图所示,四边形ABCD中,
∠A+∠C= 180°
∵∠A+∠B+ ∠C+ ∠D=(4-2)×180。=360°
∴∠B+∠D = 360° -(∠A+∠C )
= 360° - 180°
= 180°
这就是说,如果四边形的一组对角互补,那么另一组对角也互补。 例2 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
分析:
1.任意一个外角和他相邻的内角有什么关系?
2.五个外角加上他们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系? 6 例2 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
解:5边形外角和 结论:五边形的外角和等于360°
-(5-2) × 180°
=360 ° 6=5个平角-5边形内角和
=5×180°探究 如果将例2中五边形换成n边(n≥3)
可以得到同样的结果吗?n边形外角和=结论:
n边形的外角和等于360°-(n-2) × 180°=360 °n个平角-n边形内角和=n×180 °课堂练习:练一练练习1:如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____。12n×30°=360°n=12n边形外角和=360 °练一练练习2:正五边形的每一个外角等于____,每一个内角等于_____。5X=360°X=72°72°144°解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:所以每一个内角度数为108 °练习. 已知一个多边形,它的内角和等于外角和,它是几边形? 解: 设多边形的边数为n
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360o,
∴ (n-2)?180°= 360o。
解得: n=4
∴这个多边形的边数为4。
感悟与反思n边形内角和=(n-2) ·180°n边形外角和=360°n边形外角和= n个平角-n边形内角和 通过这节课的学习你有哪些收获? 作 业
P84习题7.3 的2、6题 再见
