湖南省长沙市一中2009-2010学年高二下学期第二次学业水平模拟考试数
文档属性
| 名称 | 湖南省长沙市一中2009-2010学年高二下学期第二次学业水平模拟考试数 | 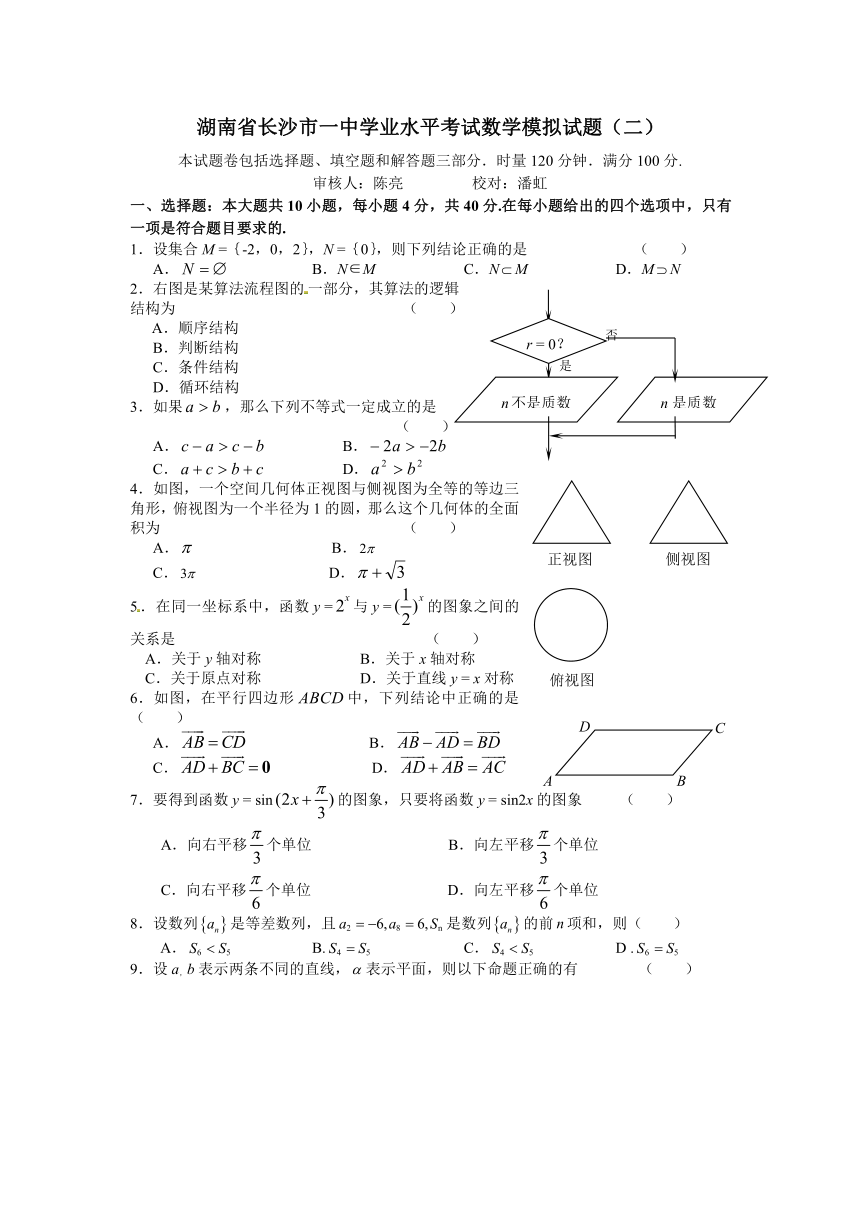 | |
| 格式 | rar | ||
| 文件大小 | 233.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-07-15 16:02:23 | ||
图片预览




文档简介
湖南省长沙市一中学业水平考试数学模拟试题(二)
本试题卷包括选择题、填空题和解答题三部分.时量120分钟.满分100分.
审核人:陈亮
校对:潘虹
一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合M
={-2,0,2},N
={0},则下列结论正确的是
(
)
A.
B.N∈M
C.NM
D.MN
2.右图是某算法流程图的一部分,其算法的逻辑
结构为
(
)
A.顺序结构
B.判断结构
C.条件结构[]
D.循环结构
3.如果,那么下列不等式一定成立的是
(
)
A.
B.
C.
D.
4.如图,一个空间几何体正视图与侧视图为全等的等边三角形,俯视图为一个半径为1的圆,那么这个几何体的全面积为
(
)
A.
B.
C.
D.
5.在同一坐标系中,函数y
=与y
=的图象之间的关系是
(
)
A.关于y轴对称
B.关于x轴对称
C.关于原点对称
D.关于直线y
=
x对称
6.如图,在平行四边形中,下列结论中正确的是
(
)
A.
B.
C.
D.
7.要得到函数y
=
sin的图象,只要将函数y
=
sin2x的图象
(
)
A.向右平移个单位
B.向左平移个单位
C.向右平移个单位
D.向左平移个单位
8.设数列是等差数列,且是数列的前项和,则(
)
A.
B.
C.
D
.
9.设a,b表示两条不同的直线,表示平面,则以下命题正确的有
(
)
①;
②;
③;
④.
A.
①②
B.
①②③
C.
②③④
D.
①②④
10.若是的三边,直线与圆相离,则一定是
(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
二、填空题:本大题共5小题,每小题4分,共20分.
11.一个盒子中装有3个完全相同的小球,分别标以号码1,2,3,从中任取一球,则取出2号球的概率是
.
12.甲,乙两人在相同条件下练习射击,每人打发子弹,命中环数如下
甲
6
8
9
9
8
乙
10
7[]
9
7
7
如果选择甲、乙二人中的一个去参加比赛,你应选择__________.
13.如果,,那么等于__________.
14.已知的三边长分别为,则的值为__________.
15.当x、y满足条件时,目标函数z
=
x+3y的最大值为____
_____.
三、解答题:本大题共5小题,共40分.解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分6分)
心脏跳动时,血压在增加或减小.心脏每完成一次跳动,血压就完成一次改变,血压的最大值和最小值分别为收缩压和舒张压.设某人的血压满足函数关系式P
(t)
=
95
+
A
sin,其中P
(t)为血压(mmHg),t为时间(min),其函数图象如图所示.
(1)根据图象写出该人的血压随时间变化的函数解析式;
(2)求出该人的收缩压,舒张压及每分钟心跳的次数.
17.(本小题满分8分)
如图,在正三棱柱中,已知.
(1)求正三棱柱的体积;
(2)直线所成角的正弦值.
18.(本小题满分8分)
高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组
频数
频率
[85,95)
①
②
[95,105)
0.050
[105,115)
0.200
[115,125)
12
0.300
[125,135)
0.275
[135,145)
4
③
[145,155)
0.050
合计
④
(1)根据上面图表,①②③④处的数值分别为
,
,
,
;
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体平均数,并估计总体落在[129,155]中的概率.
19.(本小题满分8分)
已知两圆相交于点A(1,3)
,B(m,-1),两圆的圆心均在直线x-y+c=0上.
(1)求弦AB所在直线的方程;
(2)若其中一个圆的圆心在y轴上,求该圆的方程.
20.(本小题满分10分)
已知二次函数f
(x)
=
x2
–
16x
+
p
+
3.
(1)若函数在区间上存在零点,求实数p的取值范围;
(2)问是否存在常数q(q≥0),当x∈[q,10]时,的值域为区间,且的长度为
12
–
q.(注:区间[a,b](a<b)的长度为b
–
a)
湖南省长沙市一中学业水平考试数学模拟试题(二)答案
本试题卷包括选择题、填空题和解答题三部分.时量120分钟.满分100分.
审核人:陈亮
校对:潘虹
一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合M
={-2,0,2},N
={0},则下列结论正确的是
(
C
)
A.
B.N∈M
C.NM
D.MN
2.右图是某算法流程图的一部分,其算法的逻辑
结构为
(
C
)
A.顺序结构
B.判断结构
C.条件结构
D.循环结构
3.如果,那么下列不等式一定成立的是
(
C
)
A.
B.
C.
D.
4.如图,一个空间几何体正视图与侧视图为全等的等边三角形,俯视图为一个半径为1的圆,那么这个几何体的全面积为
(
C
)
A.
B.
C.
D.
【解析】由三视图知,该几何体是一个底面半径为1,高为的圆锥,所以圆锥的全面积S全
=,故选C.
5.在同一坐标系中,函数y
=与y
=的图象之间的关系是
(
A
)
A.关于y轴对称
B.关于x轴对称
C.关于原点对称
D.关于直线y
=
x对称
6.如图,在平行四边形中,下列结论中正确的是
(
D
)
A.
B.
C.
D.
7.要得到函数y
=
sin的图象,只要将函数y
=
sin2x的图象
(
D
)
A.向右平移个单位
B.向左平移个单位
C.向右平移个单位
D.向左平移个单位
8.设数列是等差数列,且是数列的前项和,则(
B
)
A.
B.
C.
D
.
【解析】由所以a5
=
a2
+
3d
=
–6
+
3×2
=
0,于是S5
=
S4
+
0
=
S4,故选B.
9.设a,b表示两条不同的直线,表示平面,则以下命题正确的有
(
A
)
①;
②;
③;
④.
A.
①②
B.
①②③
C.
②③④
D.
①②④
【解析】易知①②正确;对于③,b可能在内;对于④,a可能平行平面,故选A.
10.若是的三边,直线与圆相离,则一定是
(
C
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
【解析】由已知得,,故是钝角三角形.
二、填空题:本大题共5小题,每小题4分,共20分.
11.一个盒子中装有3个完全相同的小球,分别标以号码1,2,3,从中任取一球,则取出2号球的概率是
.
12.甲,乙两人在相同条件下练习射击,每人打发子弹,命中环数如下
甲
6
8
9
9
8
乙
10
7
9
7[]
7
[]
如果选择甲、乙二人中的一个去参加比赛,你应选择____甲______.
【解析】故选甲.
13.如果,,那么等于
.
【解析】由已知得,
14.已知的三边长分别为,则的值为.
【解析】由余弦定理得,
15.当x、y满足条件时,目标函数z
=
x+3y的最大值为_____12_____.
【解析】在直角坐标系内画出可行域为△OAB(O为原点),A,B(3,3),由图可知,最优解为B
(3,3),故Zmax
=
12.
三、解答题:本大题共5小题,共40分.解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分6分)[]
心脏跳动时,血压在增加或减小.心脏每完成一次跳动,血压就完成一次改变,血压的最大值和最小值分别为收缩压和舒张压.设某人的血压满足函数关系式P
(t)
=
95
+
A
sin,其中P
(t)为血压(mmHg),t为时间(min),其函数图象如图所示.
(1)根据图象写出该人的血压随时间变化的函数解析式;
(2)求出该人的收缩压,舒张压及每分钟心跳的次数.
【解析】(1)由图象可知,振幅A
=
120
–
95
=
25,
周期T
=,知,于是
P
(t)
=
95
+
25
sin160t.
………………………3分
(2)收缩压为95
+
25
=
120(mmHg);
舒张压为95
–
25
=
70
(mmHg),
心跳次数为=
80次.………………………6分
17.(本小题满分8分)
如图,在正三棱柱中,已知.
(1)求正三棱柱的体积;
(2)直线所成角的正弦值.
【解析】(1).
…………3分
(2)令为中点,连,则面.
再连,得为与面所成角.……………
6分
在中,,,.
故直线所成角的正弦值.
………………………8分
18.(本小题满分8分)
高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组
频数
频率
[85,95)
①
②
[95,105)
0.050
[105,115)
0.200
[115,125)
12
0.300
[125,135)
0.275
[135,145)
4
③
[145,155)
0.050
合计
④
(1)根据上面图表,①②③④处的数值分别为
,
,
,
;
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体平均数,并估计总体落在[129,155]中的概率.
【解析】(1)①1;②0.025;③
0.1;④1…………3分
(2)频率分布直方图如图.
………………………5分
(2)利用组中值算得平均数为:90×0.025
+
100×0.05
+
110×0.2
+
120×0.3
+
130×0.275
+
140×0.1
+
150×0.05
=
122.5;
故总体落在[129,155]上的概率为
×0.275
+
0.1
+
0.05
=
0.315.
………………………8分
19.(本小题满分8分)
已知两圆相交于点A(1,3)
,B(m,-1),两圆的圆心均在直线x-y+c=0上.
(1)求弦AB所在直线的方程;
(2)若其中一个圆的圆心在y轴上,求该圆的方程.
【解析】(1)由于AB的中点C在x
–
y
+
c
=
0上,得m
=
–2c
+
1
①
又由直线AB与直线x
–
y
+
c
=
0垂直,得m
–
1
=
4
②
联立①②解得m
=
5,c
=
–2,∴弦AB所在直线的方程为x
+
y
–
4
=
0.
…………4分
(2)由(1)知,两圆的圆心均在直线x
–
y
–
2
=
0上,又由题设知,所求圆的圆心E
(0,–2)半径r2
=
|EA|2
=
26,故所求的圆的方程为x2
+
(y
+
2)2
=
26(或x2
+
y2
+
4y
–
22
=
0)…8分
20.(本小题满分10分)
已知二次函数f
(x)
=
x2
–
16x
+
p
+
3.
(1)若函数在区间上存在零点,求实数p的取值范围;
(2)问是否存在常数q(q≥0),当x∈[q,10]时,的值域为区间,且的长度为
12
–
q.(注:区间[a,b](a<b)的长度为b
–
a)
【解析】(1)∵二次函数f
(x)=
x2
–
16x
+
p
+
3的对称轴是,∴函数在区间上单调递减,则函数在区间上存在零点须满足.
……………2分
即(1
+
16
+
p
+
3)(1
–
16
+
p
+
3)≤0,
解得–20≤p≤12.
………………………4分
⑵
当时,即0≤q≤6时,的值域为:[f
(8),f
(q)],即[p–61,
q2
–16q
+
p
+
3].
∴区间长度为q2
–
16q
+
p
+
3
–
(p
–
61)
=
q2
–
16q
+
64
=
12
–
q.
∴q2
–
15q
+
52
=
0
∴,经检验不合题意,舍去.……6分
当时,即6≤q<8时,的值域为:,即[p
–
61,p
–
57]
∴区间长度为p
–
57
–
(p
–
61)
=
4
=
12
–
q
∴q
=
8.经检验q
=
8不合题意,舍去.
…8分
当q≥8时,的值域为:[f
(q),f
(10)],即
[q2
–
16q
+
p
+3,p
–
57].
∴区间长度为p
–
57
–(q2
–
16q
+
p
+
3)
=
–q2
–
16q
–
60
=
12
–
q,
∴q2
–
17q
+
72
=
0
,
∴q
=
8或q
=
9.经检验q
=
8或q
=
9满足题意.
所以存在常数q
=
8或q
=
9,当x∈[q,10]时,的值域为区间,且的长度为12–q.
………………………10分
r
=
0?
否
是
n不是质数数数数
n是质数
正视图
侧视图
俯视图
B
D
C
A
r
=
0?
否
是
n是质数
n不是质数数数数
正视图
侧视图
俯视图
B
D
C
A
本试题卷包括选择题、填空题和解答题三部分.时量120分钟.满分100分.
审核人:陈亮
校对:潘虹
一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合M
={-2,0,2},N
={0},则下列结论正确的是
(
)
A.
B.N∈M
C.NM
D.MN
2.右图是某算法流程图的一部分,其算法的逻辑
结构为
(
)
A.顺序结构
B.判断结构
C.条件结构[]
D.循环结构
3.如果,那么下列不等式一定成立的是
(
)
A.
B.
C.
D.
4.如图,一个空间几何体正视图与侧视图为全等的等边三角形,俯视图为一个半径为1的圆,那么这个几何体的全面积为
(
)
A.
B.
C.
D.
5.在同一坐标系中,函数y
=与y
=的图象之间的关系是
(
)
A.关于y轴对称
B.关于x轴对称
C.关于原点对称
D.关于直线y
=
x对称
6.如图,在平行四边形中,下列结论中正确的是
(
)
A.
B.
C.
D.
7.要得到函数y
=
sin的图象,只要将函数y
=
sin2x的图象
(
)
A.向右平移个单位
B.向左平移个单位
C.向右平移个单位
D.向左平移个单位
8.设数列是等差数列,且是数列的前项和,则(
)
A.
B.
C.
D
.
9.设a,b表示两条不同的直线,表示平面,则以下命题正确的有
(
)
①;
②;
③;
④.
A.
①②
B.
①②③
C.
②③④
D.
①②④
10.若是的三边,直线与圆相离,则一定是
(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
二、填空题:本大题共5小题,每小题4分,共20分.
11.一个盒子中装有3个完全相同的小球,分别标以号码1,2,3,从中任取一球,则取出2号球的概率是
.
12.甲,乙两人在相同条件下练习射击,每人打发子弹,命中环数如下
甲
6
8
9
9
8
乙
10
7[]
9
7
7
如果选择甲、乙二人中的一个去参加比赛,你应选择__________.
13.如果,,那么等于__________.
14.已知的三边长分别为,则的值为__________.
15.当x、y满足条件时,目标函数z
=
x+3y的最大值为____
_____.
三、解答题:本大题共5小题,共40分.解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分6分)
心脏跳动时,血压在增加或减小.心脏每完成一次跳动,血压就完成一次改变,血压的最大值和最小值分别为收缩压和舒张压.设某人的血压满足函数关系式P
(t)
=
95
+
A
sin,其中P
(t)为血压(mmHg),t为时间(min),其函数图象如图所示.
(1)根据图象写出该人的血压随时间变化的函数解析式;
(2)求出该人的收缩压,舒张压及每分钟心跳的次数.
17.(本小题满分8分)
如图,在正三棱柱中,已知.
(1)求正三棱柱的体积;
(2)直线所成角的正弦值.
18.(本小题满分8分)
高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组
频数
频率
[85,95)
①
②
[95,105)
0.050
[105,115)
0.200
[115,125)
12
0.300
[125,135)
0.275
[135,145)
4
③
[145,155)
0.050
合计
④
(1)根据上面图表,①②③④处的数值分别为
,
,
,
;
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体平均数,并估计总体落在[129,155]中的概率.
19.(本小题满分8分)
已知两圆相交于点A(1,3)
,B(m,-1),两圆的圆心均在直线x-y+c=0上.
(1)求弦AB所在直线的方程;
(2)若其中一个圆的圆心在y轴上,求该圆的方程.
20.(本小题满分10分)
已知二次函数f
(x)
=
x2
–
16x
+
p
+
3.
(1)若函数在区间上存在零点,求实数p的取值范围;
(2)问是否存在常数q(q≥0),当x∈[q,10]时,的值域为区间,且的长度为
12
–
q.(注:区间[a,b](a<b)的长度为b
–
a)
湖南省长沙市一中学业水平考试数学模拟试题(二)答案
本试题卷包括选择题、填空题和解答题三部分.时量120分钟.满分100分.
审核人:陈亮
校对:潘虹
一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合M
={-2,0,2},N
={0},则下列结论正确的是
(
C
)
A.
B.N∈M
C.NM
D.MN
2.右图是某算法流程图的一部分,其算法的逻辑
结构为
(
C
)
A.顺序结构
B.判断结构
C.条件结构
D.循环结构
3.如果,那么下列不等式一定成立的是
(
C
)
A.
B.
C.
D.
4.如图,一个空间几何体正视图与侧视图为全等的等边三角形,俯视图为一个半径为1的圆,那么这个几何体的全面积为
(
C
)
A.
B.
C.
D.
【解析】由三视图知,该几何体是一个底面半径为1,高为的圆锥,所以圆锥的全面积S全
=,故选C.
5.在同一坐标系中,函数y
=与y
=的图象之间的关系是
(
A
)
A.关于y轴对称
B.关于x轴对称
C.关于原点对称
D.关于直线y
=
x对称
6.如图,在平行四边形中,下列结论中正确的是
(
D
)
A.
B.
C.
D.
7.要得到函数y
=
sin的图象,只要将函数y
=
sin2x的图象
(
D
)
A.向右平移个单位
B.向左平移个单位
C.向右平移个单位
D.向左平移个单位
8.设数列是等差数列,且是数列的前项和,则(
B
)
A.
B.
C.
D
.
【解析】由所以a5
=
a2
+
3d
=
–6
+
3×2
=
0,于是S5
=
S4
+
0
=
S4,故选B.
9.设a,b表示两条不同的直线,表示平面,则以下命题正确的有
(
A
)
①;
②;
③;
④.
A.
①②
B.
①②③
C.
②③④
D.
①②④
【解析】易知①②正确;对于③,b可能在内;对于④,a可能平行平面,故选A.
10.若是的三边,直线与圆相离,则一定是
(
C
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
【解析】由已知得,,故是钝角三角形.
二、填空题:本大题共5小题,每小题4分,共20分.
11.一个盒子中装有3个完全相同的小球,分别标以号码1,2,3,从中任取一球,则取出2号球的概率是
.
12.甲,乙两人在相同条件下练习射击,每人打发子弹,命中环数如下
甲
6
8
9
9
8
乙
10
7
9
7[]
7
[]
如果选择甲、乙二人中的一个去参加比赛,你应选择____甲______.
【解析】故选甲.
13.如果,,那么等于
.
【解析】由已知得,
14.已知的三边长分别为,则的值为.
【解析】由余弦定理得,
15.当x、y满足条件时,目标函数z
=
x+3y的最大值为_____12_____.
【解析】在直角坐标系内画出可行域为△OAB(O为原点),A,B(3,3),由图可知,最优解为B
(3,3),故Zmax
=
12.
三、解答题:本大题共5小题,共40分.解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分6分)[]
心脏跳动时,血压在增加或减小.心脏每完成一次跳动,血压就完成一次改变,血压的最大值和最小值分别为收缩压和舒张压.设某人的血压满足函数关系式P
(t)
=
95
+
A
sin,其中P
(t)为血压(mmHg),t为时间(min),其函数图象如图所示.
(1)根据图象写出该人的血压随时间变化的函数解析式;
(2)求出该人的收缩压,舒张压及每分钟心跳的次数.
【解析】(1)由图象可知,振幅A
=
120
–
95
=
25,
周期T
=,知,于是
P
(t)
=
95
+
25
sin160t.
………………………3分
(2)收缩压为95
+
25
=
120(mmHg);
舒张压为95
–
25
=
70
(mmHg),
心跳次数为=
80次.………………………6分
17.(本小题满分8分)
如图,在正三棱柱中,已知.
(1)求正三棱柱的体积;
(2)直线所成角的正弦值.
【解析】(1).
…………3分
(2)令为中点,连,则面.
再连,得为与面所成角.……………
6分
在中,,,.
故直线所成角的正弦值.
………………………8分
18.(本小题满分8分)
高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组
频数
频率
[85,95)
①
②
[95,105)
0.050
[105,115)
0.200
[115,125)
12
0.300
[125,135)
0.275
[135,145)
4
③
[145,155)
0.050
合计
④
(1)根据上面图表,①②③④处的数值分别为
,
,
,
;
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体平均数,并估计总体落在[129,155]中的概率.
【解析】(1)①1;②0.025;③
0.1;④1…………3分
(2)频率分布直方图如图.
………………………5分
(2)利用组中值算得平均数为:90×0.025
+
100×0.05
+
110×0.2
+
120×0.3
+
130×0.275
+
140×0.1
+
150×0.05
=
122.5;
故总体落在[129,155]上的概率为
×0.275
+
0.1
+
0.05
=
0.315.
………………………8分
19.(本小题满分8分)
已知两圆相交于点A(1,3)
,B(m,-1),两圆的圆心均在直线x-y+c=0上.
(1)求弦AB所在直线的方程;
(2)若其中一个圆的圆心在y轴上,求该圆的方程.
【解析】(1)由于AB的中点C在x
–
y
+
c
=
0上,得m
=
–2c
+
1
①
又由直线AB与直线x
–
y
+
c
=
0垂直,得m
–
1
=
4
②
联立①②解得m
=
5,c
=
–2,∴弦AB所在直线的方程为x
+
y
–
4
=
0.
…………4分
(2)由(1)知,两圆的圆心均在直线x
–
y
–
2
=
0上,又由题设知,所求圆的圆心E
(0,–2)半径r2
=
|EA|2
=
26,故所求的圆的方程为x2
+
(y
+
2)2
=
26(或x2
+
y2
+
4y
–
22
=
0)…8分
20.(本小题满分10分)
已知二次函数f
(x)
=
x2
–
16x
+
p
+
3.
(1)若函数在区间上存在零点,求实数p的取值范围;
(2)问是否存在常数q(q≥0),当x∈[q,10]时,的值域为区间,且的长度为
12
–
q.(注:区间[a,b](a<b)的长度为b
–
a)
【解析】(1)∵二次函数f
(x)=
x2
–
16x
+
p
+
3的对称轴是,∴函数在区间上单调递减,则函数在区间上存在零点须满足.
……………2分
即(1
+
16
+
p
+
3)(1
–
16
+
p
+
3)≤0,
解得–20≤p≤12.
………………………4分
⑵
当时,即0≤q≤6时,的值域为:[f
(8),f
(q)],即[p–61,
q2
–16q
+
p
+
3].
∴区间长度为q2
–
16q
+
p
+
3
–
(p
–
61)
=
q2
–
16q
+
64
=
12
–
q.
∴q2
–
15q
+
52
=
0
∴,经检验不合题意,舍去.……6分
当时,即6≤q<8时,的值域为:,即[p
–
61,p
–
57]
∴区间长度为p
–
57
–
(p
–
61)
=
4
=
12
–
q
∴q
=
8.经检验q
=
8不合题意,舍去.
…8分
当q≥8时,的值域为:[f
(q),f
(10)],即
[q2
–
16q
+
p
+3,p
–
57].
∴区间长度为p
–
57
–(q2
–
16q
+
p
+
3)
=
–q2
–
16q
–
60
=
12
–
q,
∴q2
–
17q
+
72
=
0
,
∴q
=
8或q
=
9.经检验q
=
8或q
=
9满足题意.
所以存在常数q
=
8或q
=
9,当x∈[q,10]时,的值域为区间,且的长度为12–q.
………………………10分
r
=
0?
否
是
n不是质数数数数
n是质数
正视图
侧视图
俯视图
B
D
C
A
r
=
0?
否
是
n是质数
n不是质数数数数
正视图
侧视图
俯视图
B
D
C
A
同课章节目录
