3.2函数模型及其应用节综合检测题(带解析)
文档属性
| 名称 | 3.2函数模型及其应用节综合检测题(带解析) | 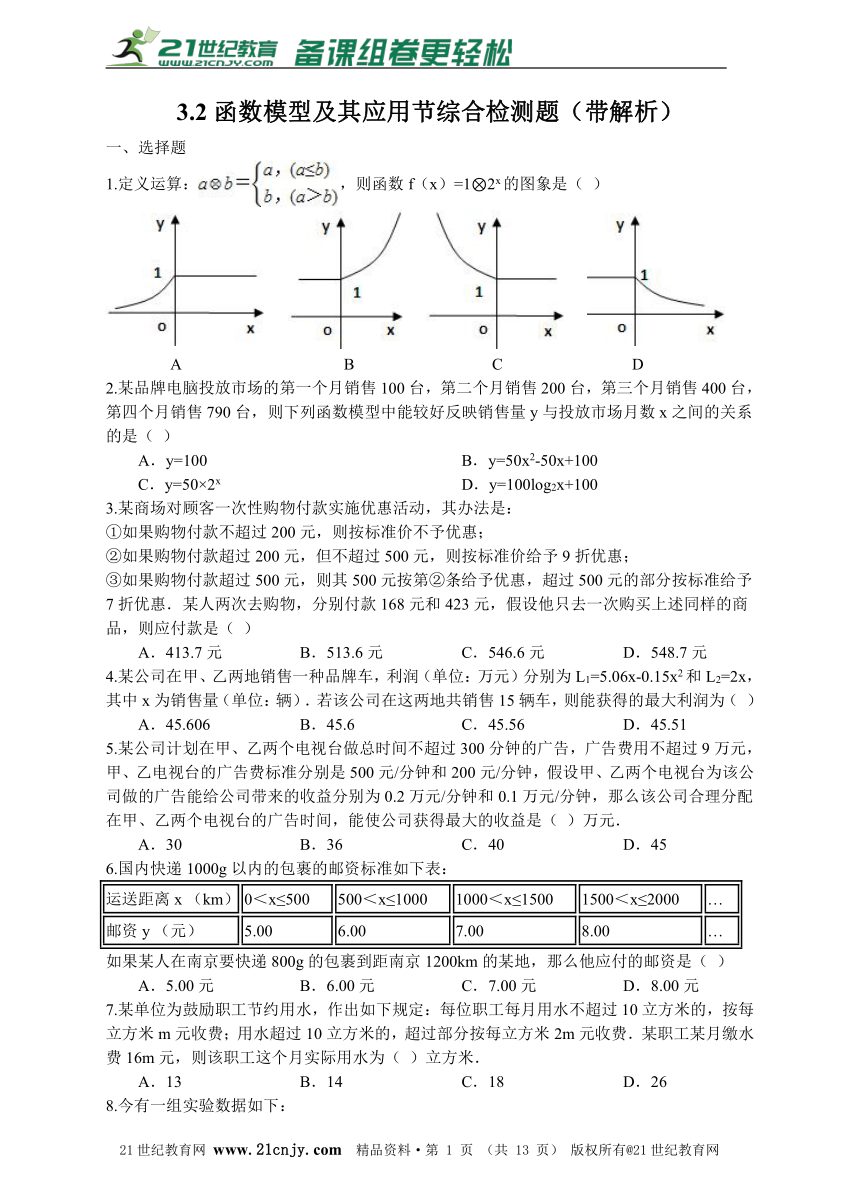 | |
| 格式 | zip | ||
| 文件大小 | 715.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-11-28 10:50:20 | ||
图片预览





文档简介
3.2函数模型及其应用节综合检测题(带解析)
一、选择题
1.定义运算:,则函数f(x)=1?2x的图象是( )
A B C D
2.某品牌电脑投放市场的第一个月销售100台,第二个月销售200台,第三个月销售400台,第四个月销售790台,则下列函数模型中能较好反映销售量y与投放市场月数x之间的关系的是( )www.21-cn-jy.com
A.y=100 B.y=50x2-50x+100 C.y=50×2x D.y=100log2x+100
3.某商场对顾客一次性购物付款实施优惠活动,其办法是: ①如果购物付款不超过200元,则按标准价不予优惠; ②如果购物付款超过200元,但不超过500元,则按标准价给予9折优惠; ③如果购物付款超过500元,则其500元按第②条给予优惠,超过500元的部分按标准给予7折优惠.某人两次去购物,分别付款168元和423元,假设他只去一次购买上述同样的商品,则应付款是( )21教育网
A.413.7元 B.513.6元 C.546.6元 D.548.7元
4.某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为L1=5.06x-0.15x2和L2=2x,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,则能获得的最大利润为( )
A.45.606 B.45.6 C.45.56 D.45.51
5.某公司计划在甲、乙两个电视台做总时间不超过300分钟的广告,广告费用不超过9万元,甲、乙电视台的广告费标准分别是500元/分钟和200元/分钟,假设甲、乙两个电视台为该公司做的广告能给公司带来的收益分别为0.2万元/分钟和0.1万元/分钟,那么该公司合理分配在甲、乙两个电视台的广告时间,能使公司获得最大的收益是( )万元.
A.30 B.36 C.40 D.45
6.国内快递1000g以内的包裹的邮资标准如下表:
运送距离x?(km)
0<x≤500
500<x≤1000
1000<x≤1500
1500<x≤2000
…
邮资y?(元)
5.00
6.00
7.00
8.00
…
如果某人在南京要快递800g的包裹到距南京1200km的某地,那么他应付的邮资是( )
A.5.00元 B.6.00元 C.7.00元 D.8.00元
7.某单位为鼓励职工节约用水,作出如下规定:每位职工每月用水不超过10立方米的,按每立方米m元收费;用水超过10立方米的,超过部分按每立方米2m元收费.某职工某月缴水费16m元,则该职工这个月实际用水为( )立方米.【来源:21·世纪·教育·网】
A.13 B.14 C.18 D.26
8.今有一组实验数据如下:
t
1.99
3.00
4.00
5.10
6.12
v
1.5
4.04
7.5
12
18.01
现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是( )
A.v=log2t B.v=t C.v= D.v=2t-2
9.中原名校本次试卷批改采用网上统一阅卷,各校选派阅卷老师时规定:每100人选1名老师,总人数除以100的余数大于70时再增加一名老师.那么各校需派出的老师数量与各校的学生数量之间的函数关系如果用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为( )21·世纪*教育网
A.y=[] B.y=[] C.y=[] D.y=[]
10.某地区居民生活用电分为高峰和低谷两个时间段进行分时计价,该地区的电网销售电价表如下:
???????? 高峰时间段用电价格表
???? 低谷时间段用电价格表
?高峰月用电量(单位:千瓦时)
?高峰电价(单位:元/千瓦时)
?低谷月用电量(单位:千瓦时)
?低谷电价(单位:元/千瓦时)
?50及以下的部分
?0.568
?50及以下的部分
?0.288
?超过50至200的部分
?0.598
?超过50至200的部分
?0.318
?超过200的部分
?0.668
?超过200的部分
?0.388
若某家庭5月份的高峰时间段用电量为200千瓦时,低谷时间段用电量为100千瓦时,则按这种计费方式该家庭本月应付的电费为( )www-2-1-cnjy-com
A.118.1元 B.128.4元 C.108.1元 D.148.4元
11.直角梯形OABC中AB∥OC、AB=1、OC=BC=2,直线l:x=t截该梯形所得位于l左边图形面积为S,则函数S=f(t)的图象大致为( )2-1-c-n-j-y
A B C D
二、填空题
12.已知函数(x∈R)的最大值为M,最小值为m,则M+m的值为?? ? .
13.已知实数a≠0,函数,若f(1-a)=f(1+a),则a的值为?? .
14.我国的人口约13亿,如果今后能将人口数年平均增长率控制在1%,那么经过x年后我国人口数为y亿,则y与x的关系式为?? . 21*cnjy*com
15.一个工厂生产某种产品每年需要固定投资100万元,此外每生产1件该产品还需要增加投资1万元,年产量为x(x∈N*)件.当x≤20时,年销售总收入为(33x-x2)万元;当x>20时,年销售总收入为260万元.记该工厂生产并销售这种产品所得的年利润为y万元,则y(万元)与x(件)的函数关系式为? ?? ,该工厂的年产量为??? 件时,所得年利润最大.(年利润=年销售总收入-年总投资)【来源:21cnj*y.co*m】
16.如图给出了描述某池塘中的浮萍蔓延的面积y(m2)与时间t(月)关系的散点图.有以下叙述: ①与函数y=t2+1相比,函数y=2t作为近似刻画y与t的函数关系的模型更好; ②按图中数据显现出的趋势,第5个月时,浮萍的面积就会超过30m2; ③按图中数据显现出的趋势,浮萍从2月的4m2蔓延到16m2至少需要经过3个月; ④按图中数据显现出的趋势,浮萍每个月增加的面积约是上个月增加面积的两倍,其中正确的说法是? ?? .【出处:21教育名师】
三、解答题
17.20世纪90年代,气候变化专业委员会向政府提供的一项报告指出:全球气候逐年变暖的一个重要因素是人类在能源利用与森林砍伐中使CO2体积分数增加.据测,1990年、1991年、1992年大气中的CO2体积分数分别比1989年增加了1个可比单位、3个可比单位、6个可比单位.若用一个函数模拟20世纪90年代中每年CO2体积分数增加的可比单位数y与年份增加数x(即当年数与1989的差)的关系,模拟函数可选用二次函数f(x)=px2+qx+r(其中p,q,r为常数)或函数?g(x)=abx+c(其中a,b,c为常数,且b>0,b≠1), (1)根据题中的数据,求f(x)和g(x)的解析式; (2)如果1994年大气中的CO2体积分数比1989年增加了16个可比单位,请问用以上哪个函数作为模拟函数较好?并说明理由.【版权所有:21教育】
18.某旅游点有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元.根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超出6元,则每超过1元,租不出的自行车就增加3辆. 为了便于结算,每辆自行车的日租金x(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用y(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得). (1)求函数y=f(x)的解析式及其定义域; (2)试问当每辆自行车的日租金为多少元时,才能使一日的净收入最多?
19.心理学家发现,学生的接受能力依赖于老师引入概念和描述问题所用的时间,上课开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,并趋于稳定.分析结果和实验表明,设提出和讲述概念的时间为x(单位:分),学生的接受能力为f(x)(f(x)值越大,表示接受能力越强), (1)开讲后多少分钟,学生的接受能力最强?能维持多少时间? (2)试比较开讲后5分钟、20分钟、35分钟,学生的接受能力的大小; (3)若一个数学难题,需要56的接受能力以及12分钟时间,老师能否及时在学生一直达到所需接受能力的状态下讲述完这个难题?21cnjy.com
20.根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.
t/天
5
15
20
30
Q/件
35
25
20
10
(1)根据图象,写出该产品每件销售价格P与时间t的函数解析式; (2)在所给的直角坐标系中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销售量Q与时间t的一个函数解析式; (3)在这30天内,哪一天的日销售金额最大?(日销售金额=每件产品销售价格×日销售量)21·cn·jy·com
参考答案及解析
1.A 【解析】由已知新运算a?b的意义就是取得a,b中的最小值,因此函数f(x)4.B 【解析】依题意,可设甲销售x辆,则乙销售(15-x)辆, ∴总利润S=5.06x-0.15x2+2(15-x) =-0.15x2+3.06x+30(x≥0). ∴当x=10.2时,S取最大值 又x必须是整数,故x=10,此时Smax=45.6(万元). 5.C21世纪教育网版权所有
【解析】利用线性规划的思想方法解决,先列出约束条件,写出目标函数,作出可行域,利用图象,即可得到结论. 2·1·c·n·j·y
设公司在甲电视台和乙电视台做广告的时间分别为x分钟和y分钟,总收益为z元,由题意
∵1200∈(1000,1500] ∴y=7.00 7.A 【解析】设该职工这个月实际用水为x立方米, ∵每位职工每月用水不超过10立方米的,按每立方米m元水费收费 ∴用水不超过10立方米的缴水费不超过10m元 ∵该职工这个月缴水费16m元 ∴该职工这个月实际用水超过10立方米,超过部分的水费=(x-10)×2m, ∴由题意可列出一元一次方程式:10m+(x-10)×2m=16m 解得:x=13 8.C 【解析】当t=4时, A、v=log24=2,故选项错误; B、v=4=-2,,故选项错误; C、v==7.5.故选项正确; D、v=2×4-2=6,故选项错误; 9.B 【解析】设取整函数为y=[],则 结合不同段上函数的性质,可知选项C符合. 12.2 【解析】函数=1- ∵y=x3为奇函数,y=3|x|+1为偶函数 故函数y=为奇函数, 设函数y=的最大值N和最小值n 则N+n=0 则M=1-n,m=1-M 故M+m=(1-n)+(1-M)=2-(N+n)=2 13. 【解析】当a>0时,1-a<1,1+a>1 ∴2(1-a)+a=-1-a-2a解得a=舍去 当a<0时,1-a>1,1+a<1 当x≤20时,y=-x2+32x-100=-(x-16)2+156,∴x=16时,y取得最大值156万元; 当x>20时,y=160-x<140万元 ∵156>140,∴x=16时,利润最大值156万元 16.①②④ 【解析】①由题意可知:浮萍蔓延的面积(m2)与时间(月)的关系:y=ax(a>0且a≠1),且由函数图象可知函数过点(1,2),∴a=2,∴这个指数函数的底数是2正确,故①正确; ∴函数的解析式为:y=2x, ②当x=5 时,y=25=32>30,故第5个月时,浮萍的面积就会超过30m2成立,故②正确; ③由y=2x知,x=2,y=4,x=4,y=16,即需要经过2个月,故③不正确; ④由y=2x知,浮萍每个月增加的面积约是上个月增加面积的两倍, 17.(1), (2)选用作为模拟函数较好 【解析】(1)根据题中的数据,得:和,
解得:和, ∴,. (2)∵f(5)=15,g(5)=17.25, f(5)更接近于16, ∴选用作为模拟函数较好 18.(1)y= ∵270>185, ∴当每辆自行车的日租金定在11元时,才能使一日的净收入最多. 19.(1)开讲后10分钟,学生的接受能力最强,并能维持5分钟 (2)开讲后5分钟、20分钟、35分钟的接受能力 (3)老师不能在所需的接受能力和时间状态下讲述完这个难题. 【解析】(1)由题意可知:0<x≤10 f(x)=-0.1(x-13)2+60.9 所以当x=10时,f(x)的最大值是60,…(2分) 又10<x≤15,f(x)=60??????????????…(3分) 所以开讲后10分钟,学生的接受能力最强,并能维持5分钟.…(4分) (2)由题意可知:f(5)=54.5,f(20)=45,f(35)=30?…(5分) 所以开讲后5分钟、20分钟、35分钟的学生的接受能力从大小依次是 开讲后5分钟、20分钟、35分钟的接受能力;…(6分) (3)由题意可知: 当0<x≤10,f(x)=-0.1(x-13)2+60.9≥56 解得:6≤x≤10?????????????????…(7分) 当10<x≤15时,f(x)=60>56,满足要求;?…(8分) 当15<x≤25时,-3x+105≥56 解得:15<x≤16????????????????…(9分)
从图象发现:点(5,35),(15,25),(20,20),(30,10) 可能在同一直线上.设它们所在直线l的解析式为Q=kt+b(k、b为常数), 将点(5,35),(30,10)代入方程得 解得k=-1,b=40,所以Q=-t+40, 检验点(15,25),(20,20)也适合该式,因此日销售量Q与时间t的一个解析式为 Q=-t+40(0<t≤30,t∈N+); (3)设日销售金额为y(元),则 = 若0<t≤20,t∈N+,y=-t2+10t+1200=-(t-5)2+1225, 所以当t=5时,ymax=1225; 若20<t≤30,t∈N+,y=-50t+2000是减函数,所以y<-50×20+2000=1000. 因此,这种产品在第5天的日销售金额最大,最大日销售金额是1225元.
一、选择题
1.定义运算:,则函数f(x)=1?2x的图象是( )
A B C D
2.某品牌电脑投放市场的第一个月销售100台,第二个月销售200台,第三个月销售400台,第四个月销售790台,则下列函数模型中能较好反映销售量y与投放市场月数x之间的关系的是( )www.21-cn-jy.com
A.y=100 B.y=50x2-50x+100 C.y=50×2x D.y=100log2x+100
3.某商场对顾客一次性购物付款实施优惠活动,其办法是: ①如果购物付款不超过200元,则按标准价不予优惠; ②如果购物付款超过200元,但不超过500元,则按标准价给予9折优惠; ③如果购物付款超过500元,则其500元按第②条给予优惠,超过500元的部分按标准给予7折优惠.某人两次去购物,分别付款168元和423元,假设他只去一次购买上述同样的商品,则应付款是( )21教育网
A.413.7元 B.513.6元 C.546.6元 D.548.7元
4.某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为L1=5.06x-0.15x2和L2=2x,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,则能获得的最大利润为( )
A.45.606 B.45.6 C.45.56 D.45.51
5.某公司计划在甲、乙两个电视台做总时间不超过300分钟的广告,广告费用不超过9万元,甲、乙电视台的广告费标准分别是500元/分钟和200元/分钟,假设甲、乙两个电视台为该公司做的广告能给公司带来的收益分别为0.2万元/分钟和0.1万元/分钟,那么该公司合理分配在甲、乙两个电视台的广告时间,能使公司获得最大的收益是( )万元.
A.30 B.36 C.40 D.45
6.国内快递1000g以内的包裹的邮资标准如下表:
运送距离x?(km)
0<x≤500
500<x≤1000
1000<x≤1500
1500<x≤2000
…
邮资y?(元)
5.00
6.00
7.00
8.00
…
如果某人在南京要快递800g的包裹到距南京1200km的某地,那么他应付的邮资是( )
A.5.00元 B.6.00元 C.7.00元 D.8.00元
7.某单位为鼓励职工节约用水,作出如下规定:每位职工每月用水不超过10立方米的,按每立方米m元收费;用水超过10立方米的,超过部分按每立方米2m元收费.某职工某月缴水费16m元,则该职工这个月实际用水为( )立方米.【来源:21·世纪·教育·网】
A.13 B.14 C.18 D.26
8.今有一组实验数据如下:
t
1.99
3.00
4.00
5.10
6.12
v
1.5
4.04
7.5
12
18.01
现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是( )
A.v=log2t B.v=t C.v= D.v=2t-2
9.中原名校本次试卷批改采用网上统一阅卷,各校选派阅卷老师时规定:每100人选1名老师,总人数除以100的余数大于70时再增加一名老师.那么各校需派出的老师数量与各校的学生数量之间的函数关系如果用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为( )21·世纪*教育网
A.y=[] B.y=[] C.y=[] D.y=[]
10.某地区居民生活用电分为高峰和低谷两个时间段进行分时计价,该地区的电网销售电价表如下:
???????? 高峰时间段用电价格表
???? 低谷时间段用电价格表
?高峰月用电量(单位:千瓦时)
?高峰电价(单位:元/千瓦时)
?低谷月用电量(单位:千瓦时)
?低谷电价(单位:元/千瓦时)
?50及以下的部分
?0.568
?50及以下的部分
?0.288
?超过50至200的部分
?0.598
?超过50至200的部分
?0.318
?超过200的部分
?0.668
?超过200的部分
?0.388
若某家庭5月份的高峰时间段用电量为200千瓦时,低谷时间段用电量为100千瓦时,则按这种计费方式该家庭本月应付的电费为( )www-2-1-cnjy-com
A.118.1元 B.128.4元 C.108.1元 D.148.4元
11.直角梯形OABC中AB∥OC、AB=1、OC=BC=2,直线l:x=t截该梯形所得位于l左边图形面积为S,则函数S=f(t)的图象大致为( )2-1-c-n-j-y
A B C D
二、填空题
12.已知函数(x∈R)的最大值为M,最小值为m,则M+m的值为?? ? .
13.已知实数a≠0,函数,若f(1-a)=f(1+a),则a的值为?? .
14.我国的人口约13亿,如果今后能将人口数年平均增长率控制在1%,那么经过x年后我国人口数为y亿,则y与x的关系式为?? . 21*cnjy*com
15.一个工厂生产某种产品每年需要固定投资100万元,此外每生产1件该产品还需要增加投资1万元,年产量为x(x∈N*)件.当x≤20时,年销售总收入为(33x-x2)万元;当x>20时,年销售总收入为260万元.记该工厂生产并销售这种产品所得的年利润为y万元,则y(万元)与x(件)的函数关系式为? ?? ,该工厂的年产量为??? 件时,所得年利润最大.(年利润=年销售总收入-年总投资)【来源:21cnj*y.co*m】
16.如图给出了描述某池塘中的浮萍蔓延的面积y(m2)与时间t(月)关系的散点图.有以下叙述: ①与函数y=t2+1相比,函数y=2t作为近似刻画y与t的函数关系的模型更好; ②按图中数据显现出的趋势,第5个月时,浮萍的面积就会超过30m2; ③按图中数据显现出的趋势,浮萍从2月的4m2蔓延到16m2至少需要经过3个月; ④按图中数据显现出的趋势,浮萍每个月增加的面积约是上个月增加面积的两倍,其中正确的说法是? ?? .【出处:21教育名师】
三、解答题
17.20世纪90年代,气候变化专业委员会向政府提供的一项报告指出:全球气候逐年变暖的一个重要因素是人类在能源利用与森林砍伐中使CO2体积分数增加.据测,1990年、1991年、1992年大气中的CO2体积分数分别比1989年增加了1个可比单位、3个可比单位、6个可比单位.若用一个函数模拟20世纪90年代中每年CO2体积分数增加的可比单位数y与年份增加数x(即当年数与1989的差)的关系,模拟函数可选用二次函数f(x)=px2+qx+r(其中p,q,r为常数)或函数?g(x)=abx+c(其中a,b,c为常数,且b>0,b≠1), (1)根据题中的数据,求f(x)和g(x)的解析式; (2)如果1994年大气中的CO2体积分数比1989年增加了16个可比单位,请问用以上哪个函数作为模拟函数较好?并说明理由.【版权所有:21教育】
18.某旅游点有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元.根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超出6元,则每超过1元,租不出的自行车就增加3辆. 为了便于结算,每辆自行车的日租金x(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用y(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得). (1)求函数y=f(x)的解析式及其定义域; (2)试问当每辆自行车的日租金为多少元时,才能使一日的净收入最多?
19.心理学家发现,学生的接受能力依赖于老师引入概念和描述问题所用的时间,上课开始时,学生的兴趣激增,中间有一段不太长的时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,并趋于稳定.分析结果和实验表明,设提出和讲述概念的时间为x(单位:分),学生的接受能力为f(x)(f(x)值越大,表示接受能力越强), (1)开讲后多少分钟,学生的接受能力最强?能维持多少时间? (2)试比较开讲后5分钟、20分钟、35分钟,学生的接受能力的大小; (3)若一个数学难题,需要56的接受能力以及12分钟时间,老师能否及时在学生一直达到所需接受能力的状态下讲述完这个难题?21cnjy.com
20.根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.
t/天
5
15
20
30
Q/件
35
25
20
10
(1)根据图象,写出该产品每件销售价格P与时间t的函数解析式; (2)在所给的直角坐标系中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销售量Q与时间t的一个函数解析式; (3)在这30天内,哪一天的日销售金额最大?(日销售金额=每件产品销售价格×日销售量)21·cn·jy·com
参考答案及解析
1.A 【解析】由已知新运算a?b的意义就是取得a,b中的最小值,因此函数f(x)4.B 【解析】依题意,可设甲销售x辆,则乙销售(15-x)辆, ∴总利润S=5.06x-0.15x2+2(15-x) =-0.15x2+3.06x+30(x≥0). ∴当x=10.2时,S取最大值 又x必须是整数,故x=10,此时Smax=45.6(万元). 5.C21世纪教育网版权所有
【解析】利用线性规划的思想方法解决,先列出约束条件,写出目标函数,作出可行域,利用图象,即可得到结论. 2·1·c·n·j·y
设公司在甲电视台和乙电视台做广告的时间分别为x分钟和y分钟,总收益为z元,由题意
∵1200∈(1000,1500] ∴y=7.00 7.A 【解析】设该职工这个月实际用水为x立方米, ∵每位职工每月用水不超过10立方米的,按每立方米m元水费收费 ∴用水不超过10立方米的缴水费不超过10m元 ∵该职工这个月缴水费16m元 ∴该职工这个月实际用水超过10立方米,超过部分的水费=(x-10)×2m, ∴由题意可列出一元一次方程式:10m+(x-10)×2m=16m 解得:x=13 8.C 【解析】当t=4时, A、v=log24=2,故选项错误; B、v=4=-2,,故选项错误; C、v==7.5.故选项正确; D、v=2×4-2=6,故选项错误; 9.B 【解析】设取整函数为y=[],则 结合不同段上函数的性质,可知选项C符合. 12.2 【解析】函数=1- ∵y=x3为奇函数,y=3|x|+1为偶函数 故函数y=为奇函数, 设函数y=的最大值N和最小值n 则N+n=0 则M=1-n,m=1-M 故M+m=(1-n)+(1-M)=2-(N+n)=2 13. 【解析】当a>0时,1-a<1,1+a>1 ∴2(1-a)+a=-1-a-2a解得a=舍去 当a<0时,1-a>1,1+a<1 当x≤20时,y=-x2+32x-100=-(x-16)2+156,∴x=16时,y取得最大值156万元; 当x>20时,y=160-x<140万元 ∵156>140,∴x=16时,利润最大值156万元 16.①②④ 【解析】①由题意可知:浮萍蔓延的面积(m2)与时间(月)的关系:y=ax(a>0且a≠1),且由函数图象可知函数过点(1,2),∴a=2,∴这个指数函数的底数是2正确,故①正确; ∴函数的解析式为:y=2x, ②当x=5 时,y=25=32>30,故第5个月时,浮萍的面积就会超过30m2成立,故②正确; ③由y=2x知,x=2,y=4,x=4,y=16,即需要经过2个月,故③不正确; ④由y=2x知,浮萍每个月增加的面积约是上个月增加面积的两倍, 17.(1), (2)选用作为模拟函数较好 【解析】(1)根据题中的数据,得:和,
解得:和, ∴,. (2)∵f(5)=15,g(5)=17.25, f(5)更接近于16, ∴选用作为模拟函数较好 18.(1)y= ∵270>185, ∴当每辆自行车的日租金定在11元时,才能使一日的净收入最多. 19.(1)开讲后10分钟,学生的接受能力最强,并能维持5分钟 (2)开讲后5分钟、20分钟、35分钟的接受能力 (3)老师不能在所需的接受能力和时间状态下讲述完这个难题. 【解析】(1)由题意可知:0<x≤10 f(x)=-0.1(x-13)2+60.9 所以当x=10时,f(x)的最大值是60,…(2分) 又10<x≤15,f(x)=60??????????????…(3分) 所以开讲后10分钟,学生的接受能力最强,并能维持5分钟.…(4分) (2)由题意可知:f(5)=54.5,f(20)=45,f(35)=30?…(5分) 所以开讲后5分钟、20分钟、35分钟的学生的接受能力从大小依次是 开讲后5分钟、20分钟、35分钟的接受能力;…(6分) (3)由题意可知: 当0<x≤10,f(x)=-0.1(x-13)2+60.9≥56 解得:6≤x≤10?????????????????…(7分) 当10<x≤15时,f(x)=60>56,满足要求;?…(8分) 当15<x≤25时,-3x+105≥56 解得:15<x≤16????????????????…(9分)
从图象发现:点(5,35),(15,25),(20,20),(30,10) 可能在同一直线上.设它们所在直线l的解析式为Q=kt+b(k、b为常数), 将点(5,35),(30,10)代入方程得 解得k=-1,b=40,所以Q=-t+40, 检验点(15,25),(20,20)也适合该式,因此日销售量Q与时间t的一个解析式为 Q=-t+40(0<t≤30,t∈N+); (3)设日销售金额为y(元),则 = 若0<t≤20,t∈N+,y=-t2+10t+1200=-(t-5)2+1225, 所以当t=5时,ymax=1225; 若20<t≤30,t∈N+,y=-50t+2000是减函数,所以y<-50×20+2000=1000. 因此,这种产品在第5天的日销售金额最大,最大日销售金额是1225元.
