2.2.3直线与平面平行的性质

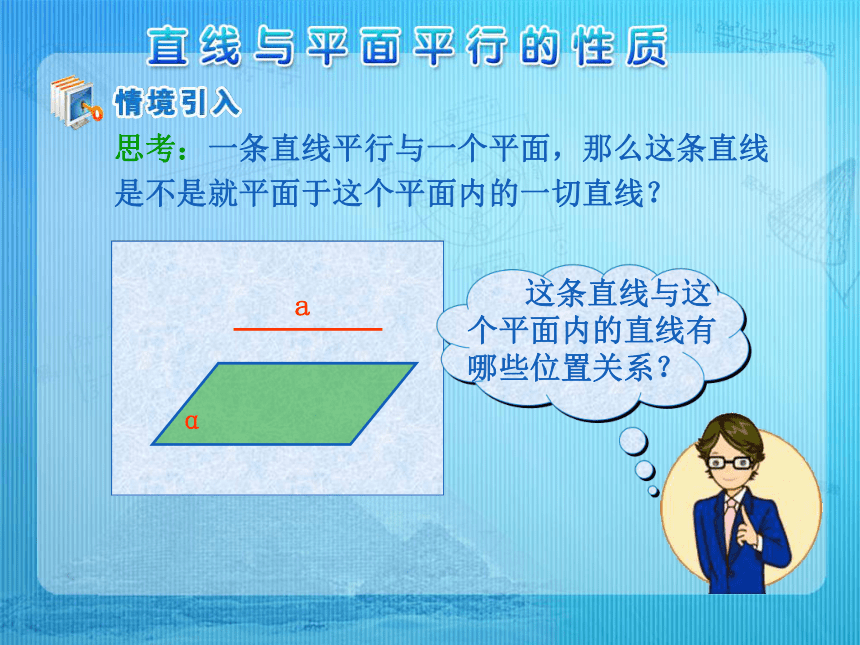
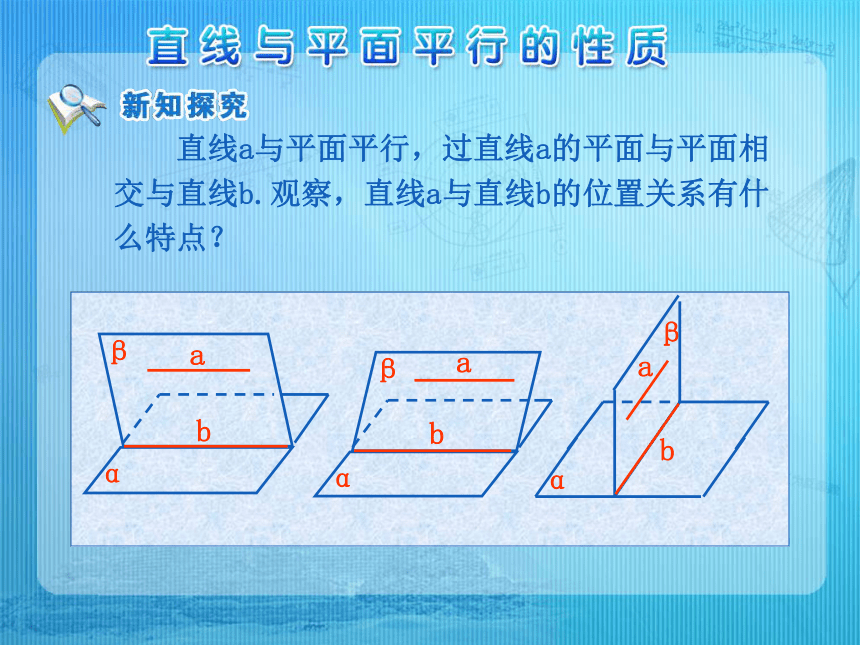
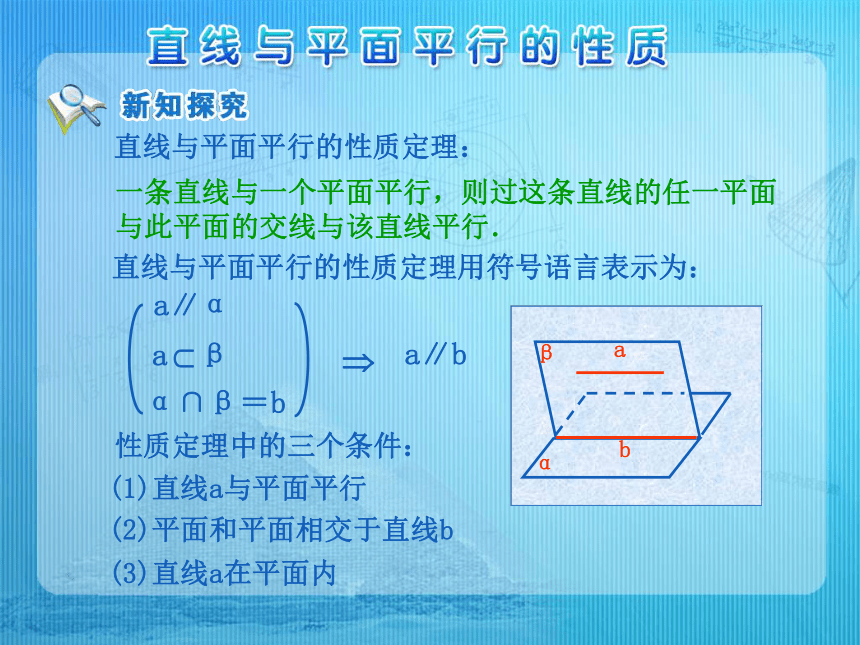
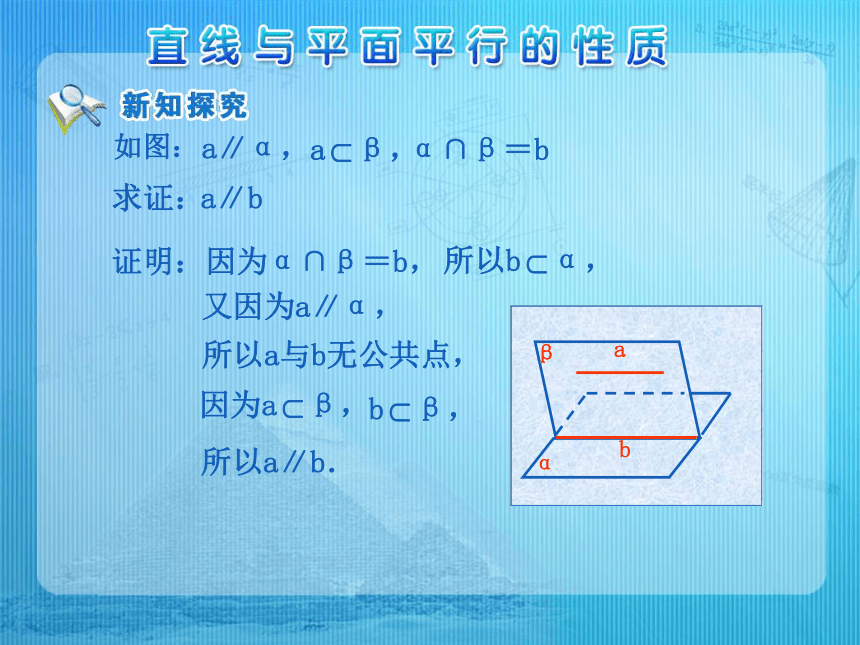
课件11张PPT。思考：一条直线平行与一个平面，那么这条直线是不是就平面于这个平面内的一切直线？　　直线a与平面平行，过直线a的平面与平面相交与直线b.观察，直线a与直线b的位置关系有什么特点？直线与平面平行的性质定理：一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行． 直线与平面平行的性质定理用符号语言表示为： a∥α α∩β＝b Ta∥b 性质定理中的三个条件： (1)直线a与平面平行 (2)平面和平面相交于直线b (3)直线a在平面内 如图：a∥α，α∩β＝b a∥b 求证： 证明：因为α∩β＝b， 又因为a∥α， 所以a与b无公共点， 所以a∥b． 讨论：教室内日光灯管所在的直线与地面平行，如何在地面上作一条直线与灯管所在的直线平行？　　由灯管两端向地面
引两条平行线，过两条
平行线与地面的交点的
连线就是与灯管平行的
直线． 已知平面外的两条平行直线中的一条平行于这个平面证明：过a作β平面，使它与α平面相交，交线为c 所以b∥α． βcα∩β＝c 所以a∥c． 因为a∥b， 所以b∥c．如图，已知直线a，b，平面α，且a∥b，a∥α，
a，b都在平面α外.求证：另一条也平行于这个平面.因为a∥α， (1)已知直线∥平面，m为平面内任一直线，则直
线与直线m的位置关系是（ ）． A：平行 B：异面 C：相交 D：平行或异面(2)一条直线若同时平行于两个相交平面，那么
这条直线与这两个平面的交线的位置关系是（ ）．A：异面 B：相交 C：平行 D：不能确定(3)若直线a、b均平行于平面，则a与b的关系是
（ ）．A：平行 B：相交 C：异面 D：平行或异面或相交DCD如图：α∩β＝CD， β∩γ＝AB, CD∥EF 求证： 证明：因为β∩γ＝AB， 又因为AB∥α， α∩γ＝EF， AB∥α． 又因为α∩β＝CD，所以AB∥CD． 同理，AB∥EF， 于是CD∥EF． 我国最早的女数学家班昭 　　我国最早的女数学家班昭，字惠
班，东汉安陵人(今陕西省咸阳县人)，
是班彪的女儿，班固的妹妹．　　班昭精通数学，汉和帝时奉召入
宫，负责教皇后和妃子的天文、数学。
公元92年，其兄班固逝世，遗留下了未完成的
《汉书》，其中的《文表》、《天文志》等篇
就是由班昭亲自完成的．大学问家马融是她的
学生，大数学家郑玄也是她的学生．他们都是
“博极群书，兼精算术”的著名学者．班昭