图形的位似（共1课时）

位似图形
一、学习目标
1、了解位似图形及其有关概念；
2、了解位似图形上任意一对对应点到位似中心的距离之比等于位似比。
3、利用图形的位似解决一些简单的实际问题；
4、在有关的学习和运用过程中发展学生的应用意识和动手操作能力。
二、基础学习
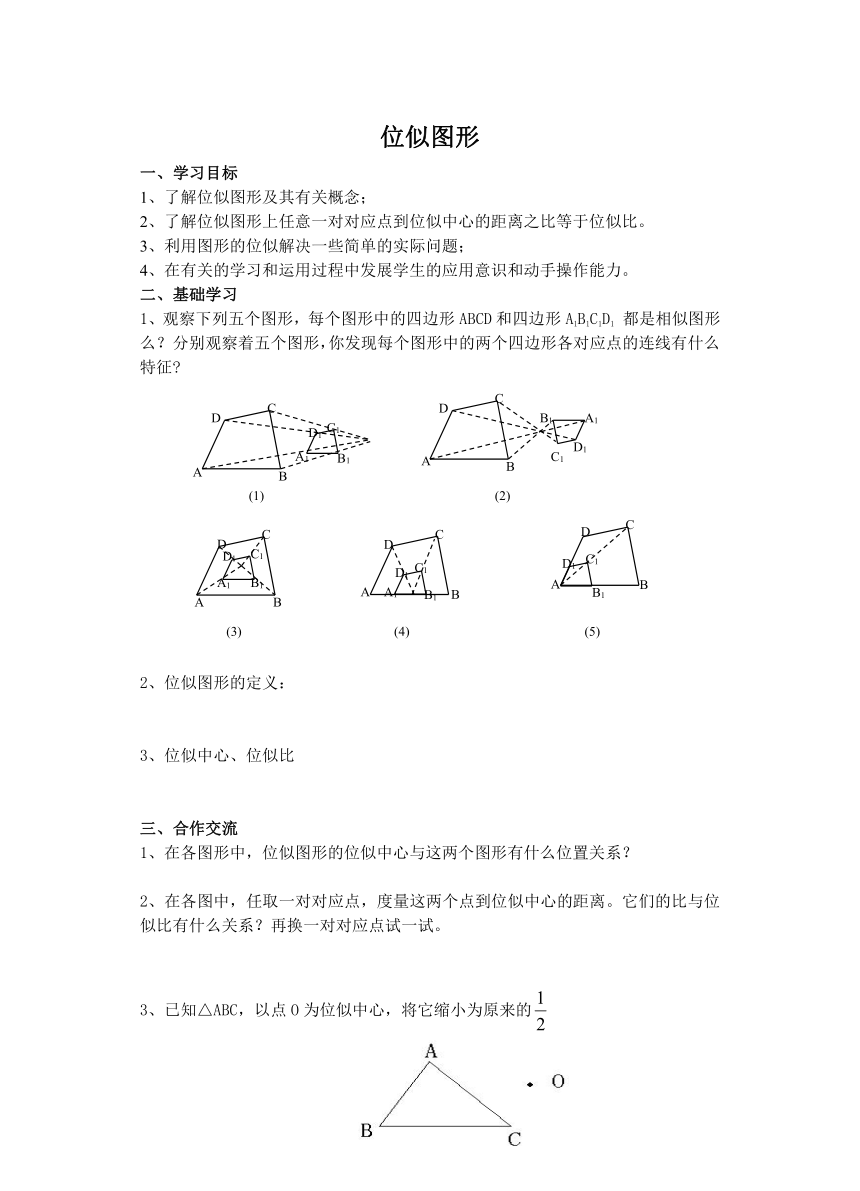
1、观察下列五个图形，每个图形中的四边形ABCD和四边形A1B1C1D1 都是相似图形么？分别观察着五个图形，你发现每个图形中的两个四边形各对应点的连线有什么特征
2、位似图形的定义：
3、位似中心、位似比
三、合作交流
1、在各图形中，位似图形的位似中心与这两个图形有什么位置关系？
2、在各图中，任取一对对应点，度量这两个点到位似中心的距离。它们的比与位似比有什么关系？再换一对对应点试一试。
3、已知△ABC，以点O为位似中心，将它缩小为原来的
四、释疑解难
如图，D，E分别是AB，AC上的点。
(1)如果DE∥BC,那么△ADE和△ABC位似图形吗 为什么
(2)如果△ADE和△ABC是位似图形,那么DE∥BC吗 为什么
五、课堂检测
1、如果两个位似图形的每组________所在的直线都_________，那么这样的两个图形叫做位似图形，这个点叫做________，这时的相似比又叫做________。
2、位似图形的对应点到位似中心的距离之比等于_____________；位似图形的对应角__________，对应线段__________（填：“相等”、“平行”、“相交”
、“在一条直线上”等）
3、位似图形的位似中心，有的在对应点连线上，有的在___________的延长线上。
4、如果两个位似图形成中心对称，那么这两个图形__________（填“一定”、“不”或“可能”等）是位似图形。
5、下列每组图形是由两个相似图形组成的，其中_____________中的两个图形是位似图形。
六、课外学习
1、完成《补充习题》
2、预习“相似三角形的应用”
A
B
C
D
B1
A1
C1
D1
B1
C1
D1
A
B
C
D
A1
B1
C1
D1
A
B
C
D
A
B
C
D
A1
B1
C1
D1
A
B
C
D
C1
A1
D1
B1
(1)
(2)
(3)
(4)
(5)
E
D
C
B
A