第一章1.6-1.7《有理数的乘方》学习指导
文档属性
| 名称 | 第一章1.6-1.7《有理数的乘方》学习指导 |

|
|
| 格式 | rar | ||
| 文件大小 | 57.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-06-07 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第一章1.6-1.7《有理数的乘方》学习指导
安徽 李师
【学习目标】
1、使学生了解乘方、幂的意义并能正确的读、写有理数的乘方;
2、掌握幂的性质并能正确地进行有理数的乘方运算。
3、能按照有理数的运算顺序正确掌握并熟练地进行有理数的混合运算。
4、掌握科学计数法,会用科学计数法表示一个数。
5、理解近似数和有效数字的意义;给一个近似数,能说出它精确到哪一位,它有几个有效数字;通过说出一个近似数的精确度和有效数字,培养把握数学文字语言,准确理解概念的能力;
6、通过乘方概念的提出,培养观察、类比、归纳及知识迁移的能力。
【重难点分析】
重点:是熟练进行有理数的乘方运算;如何按有理数的运算顺序、正确而合理地进行有理数混合运算;
难点:是理解有理数乘方运算的符号法则;熟练掌握有理数的运算顺序。
1.乘方是特殊的乘法运算,其特殊性就是相乘的因数都相同;
2.乘方运算的结果叫做幂,幂的性质是:正数的任何次幂是正数;负数的奇次幂是负数,负数的偶次幂是正数;
3.有理数的乘方运算与有理数的加减乘除一样,首先要确定幂的符号,然后再计算幂的绝对值;
4.有理数混合运算,运算时注意以下几点:
(1)先算乘方,再算乘除,最后算加减.如果有括号,就先算括号里面的.
(2)通常把六种基本的代数运算分成三级,加减是第一级运算,乘与除是第二级运算,乘方(与开方)是第三级运算.运算顺序的规定详细地讲是:先算高级运算,再算低一级运算;同级运算按从左到右的顺序进行.如果有括号先算小括号内的,再算中括号,最后算大括号.
(3)利用运算律简化运算。
(4)一个数的科学记数法中,10的指数比原数的整数位数少1.如原数有8位整数,指数就是7.
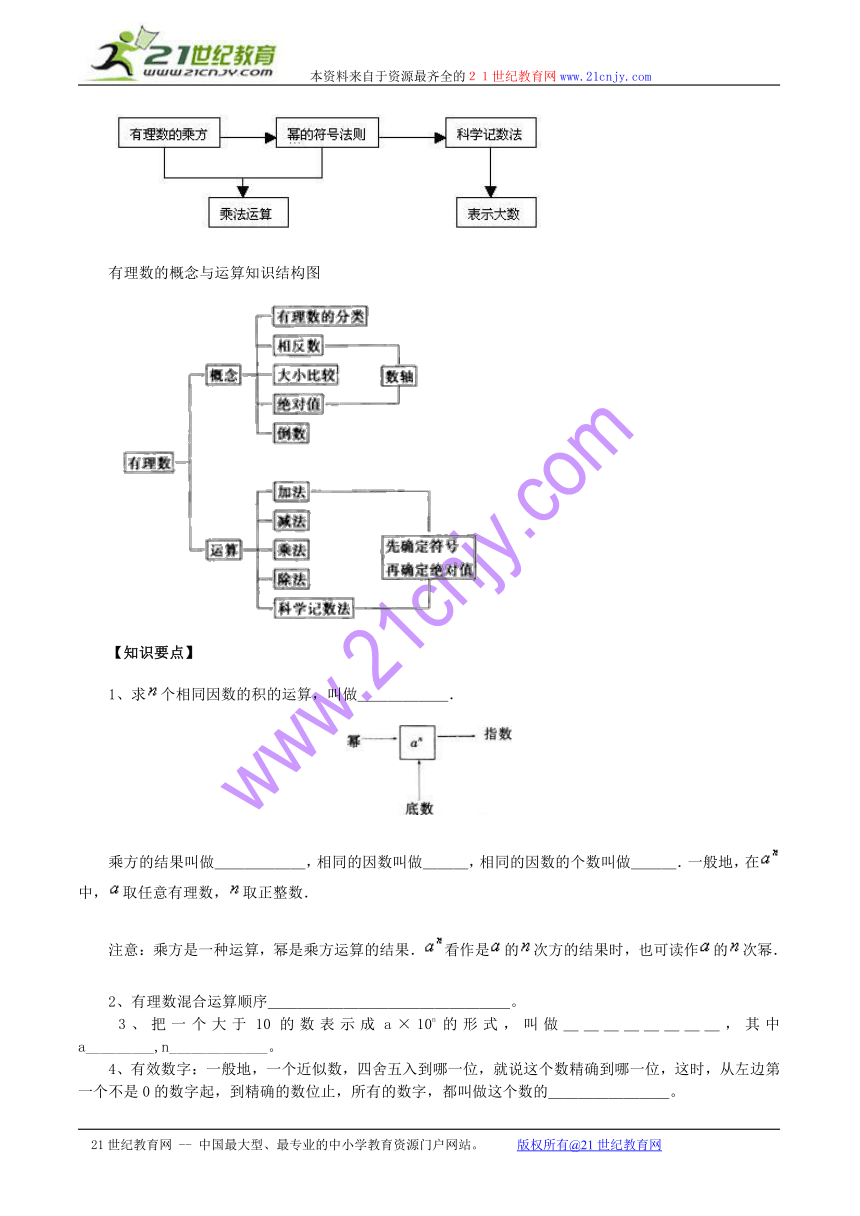
【知识结构】
有理数的概念与运算知识结构图
【知识要点】
1、求个相同因数的积的运算,叫做______.
乘方的结果叫做______,相同的因数叫做___,相同的因数的个数叫做___.一般地,在中,取任意有理数,取正整数.
注意:乘方是一种运算,幂是乘方运算的结果.看作是的次方的结果时,也可读作的次幂.
2、有理数混合运算顺序________________。
3、把一个大于10的数表示成a×10n的形式,叫做________,其中a_________,n_____________。
4、有效数字:一般地,一个近似数,四舍五入到哪一位,就说这个数精确到哪一位,这时,从左边第一个不是0的数字起,到精确的数位止,所有的数字,都叫做这个数的________。
【典型示范】
【例1】计算:
(1); (2); (3);
(4); (5); (6)。
【分析】本题意在考查对与的意义的理解,要注意二者的区别与联系。
【解】(1)。
(2)。
(3) 。
(4)。
(5)。
(6)。
【例2】计算:
(1);
(2)。
【分析】本题是乘、除、乘方混合运算。运算时一要注意运算顺序:先乘方、后乘除、二要注意每一步运算中符号的确定。
解:(1)
(2)
。
【例3】把下列各数用科学记数法表示:
(1)679000; (2)30000; (3)。
解:(1)。
(2)。
(3)。
【点评】(3)题中10的指数是原数的整数位数3减1,而不所有数位4减1。
【例4】计算:
【分析】含有括号的混合运算,一般按小、中、大括号的顺序进行运算,括号里面仍然是先进行第三级运算,再进行第二级运算,最后进行第一级运算.
【解】
【例5】下列由四舍五入得到的近似数,各精确到哪一位?各有几个有效数字?
(1)70万 (2)9.03万 (3)1.8亿 (4)6.40×105
【分析】因为这四个数都是近似数,所以
(1)的有效数字是2个:7、0,0不是个位,而是“万”位;
(2)的有效数字是3个:9、0、3,3不是百分位,而是“百”位;
(3)的有效数字是2个:1、8,8不是十分位,而是“千万”位;
(4)的有效数字是3个:6、4、0,0不是百分位,而是“千”位.
【解】(1)70万. 精确到万位,有2个有效数字7、0;
(2)9.03万.精确到百位,有3个有效数字9、0、3;
(3)1.8亿.精确到千万位,有2个有效数字1、8;
(4)6.40×105.精确到千位,有3个有效数字6、4、0.
【点评】较大的数取近似值时,常用×万,×亿等等来表示,这里的“×”表示这个近似数的有效数字,而它精确到的位数不一定是“万”或“亿”.对于不熟练的学生,应当写出原数之后再判断精确到哪一位,例如9.03万=90300,因为“3”在百位上,所以9.03万精确到百位.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第一章1.6-1.7《有理数的乘方》学习指导
安徽 李师
【学习目标】
1、使学生了解乘方、幂的意义并能正确的读、写有理数的乘方;
2、掌握幂的性质并能正确地进行有理数的乘方运算。
3、能按照有理数的运算顺序正确掌握并熟练地进行有理数的混合运算。
4、掌握科学计数法,会用科学计数法表示一个数。
5、理解近似数和有效数字的意义;给一个近似数,能说出它精确到哪一位,它有几个有效数字;通过说出一个近似数的精确度和有效数字,培养把握数学文字语言,准确理解概念的能力;
6、通过乘方概念的提出,培养观察、类比、归纳及知识迁移的能力。
【重难点分析】
重点:是熟练进行有理数的乘方运算;如何按有理数的运算顺序、正确而合理地进行有理数混合运算;
难点:是理解有理数乘方运算的符号法则;熟练掌握有理数的运算顺序。
1.乘方是特殊的乘法运算,其特殊性就是相乘的因数都相同;
2.乘方运算的结果叫做幂,幂的性质是:正数的任何次幂是正数;负数的奇次幂是负数,负数的偶次幂是正数;
3.有理数的乘方运算与有理数的加减乘除一样,首先要确定幂的符号,然后再计算幂的绝对值;
4.有理数混合运算,运算时注意以下几点:
(1)先算乘方,再算乘除,最后算加减.如果有括号,就先算括号里面的.
(2)通常把六种基本的代数运算分成三级,加减是第一级运算,乘与除是第二级运算,乘方(与开方)是第三级运算.运算顺序的规定详细地讲是:先算高级运算,再算低一级运算;同级运算按从左到右的顺序进行.如果有括号先算小括号内的,再算中括号,最后算大括号.
(3)利用运算律简化运算。
(4)一个数的科学记数法中,10的指数比原数的整数位数少1.如原数有8位整数,指数就是7.
【知识结构】
有理数的概念与运算知识结构图
【知识要点】
1、求个相同因数的积的运算,叫做______.
乘方的结果叫做______,相同的因数叫做___,相同的因数的个数叫做___.一般地,在中,取任意有理数,取正整数.
注意:乘方是一种运算,幂是乘方运算的结果.看作是的次方的结果时,也可读作的次幂.
2、有理数混合运算顺序________________。
3、把一个大于10的数表示成a×10n的形式,叫做________,其中a_________,n_____________。
4、有效数字:一般地,一个近似数,四舍五入到哪一位,就说这个数精确到哪一位,这时,从左边第一个不是0的数字起,到精确的数位止,所有的数字,都叫做这个数的________。
【典型示范】
【例1】计算:
(1); (2); (3);
(4); (5); (6)。
【分析】本题意在考查对与的意义的理解,要注意二者的区别与联系。
【解】(1)。
(2)。
(3) 。
(4)。
(5)。
(6)。
【例2】计算:
(1);
(2)。
【分析】本题是乘、除、乘方混合运算。运算时一要注意运算顺序:先乘方、后乘除、二要注意每一步运算中符号的确定。
解:(1)
(2)
。
【例3】把下列各数用科学记数法表示:
(1)679000; (2)30000; (3)。
解:(1)。
(2)。
(3)。
【点评】(3)题中10的指数是原数的整数位数3减1,而不所有数位4减1。
【例4】计算:
【分析】含有括号的混合运算,一般按小、中、大括号的顺序进行运算,括号里面仍然是先进行第三级运算,再进行第二级运算,最后进行第一级运算.
【解】
【例5】下列由四舍五入得到的近似数,各精确到哪一位?各有几个有效数字?
(1)70万 (2)9.03万 (3)1.8亿 (4)6.40×105
【分析】因为这四个数都是近似数,所以
(1)的有效数字是2个:7、0,0不是个位,而是“万”位;
(2)的有效数字是3个:9、0、3,3不是百分位,而是“百”位;
(3)的有效数字是2个:1、8,8不是十分位,而是“千万”位;
(4)的有效数字是3个:6、4、0,0不是百分位,而是“千”位.
【解】(1)70万. 精确到万位,有2个有效数字7、0;
(2)9.03万.精确到百位,有3个有效数字9、0、3;
(3)1.8亿.精确到千万位,有2个有效数字1、8;
(4)6.40×105.精确到千位,有3个有效数字6、4、0.
【点评】较大的数取近似值时,常用×万,×亿等等来表示,这里的“×”表示这个近似数的有效数字,而它精确到的位数不一定是“万”或“亿”.对于不熟练的学生,应当写出原数之后再判断精确到哪一位,例如9.03万=90300,因为“3”在百位上,所以9.03万精确到百位.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
