平面与圆锥面的截线
图片预览


文档简介
课件29张PPT。 第三讲
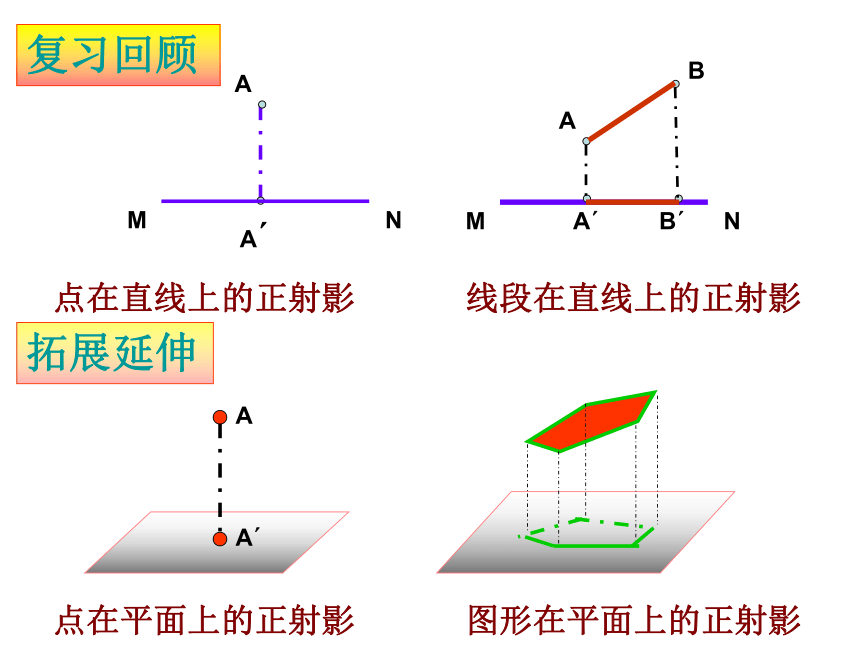
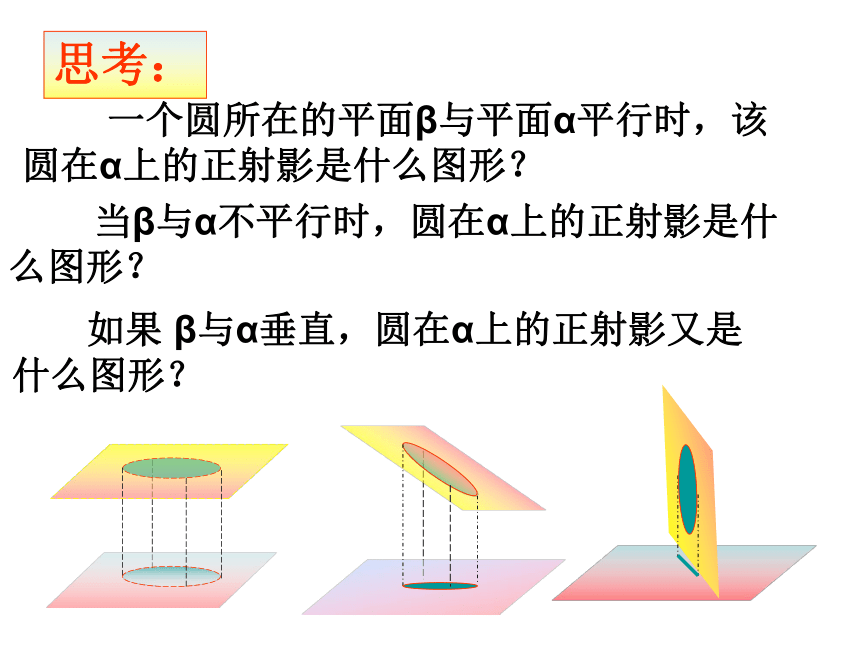
圆锥曲线性质的探讨一.平行射影复习回顾点在直线上的正射影 线段在直线上的正射影 点在平面上的正射影 拓展延伸AA′图形在平面上的正射影 一个圆所在的平面β与平面α平行时,该圆在α上的正射影是什么图形? 当β与α不平行时,圆在α上的正射影是什么图形? 如果 β与α垂直,圆在α上的正射影又是
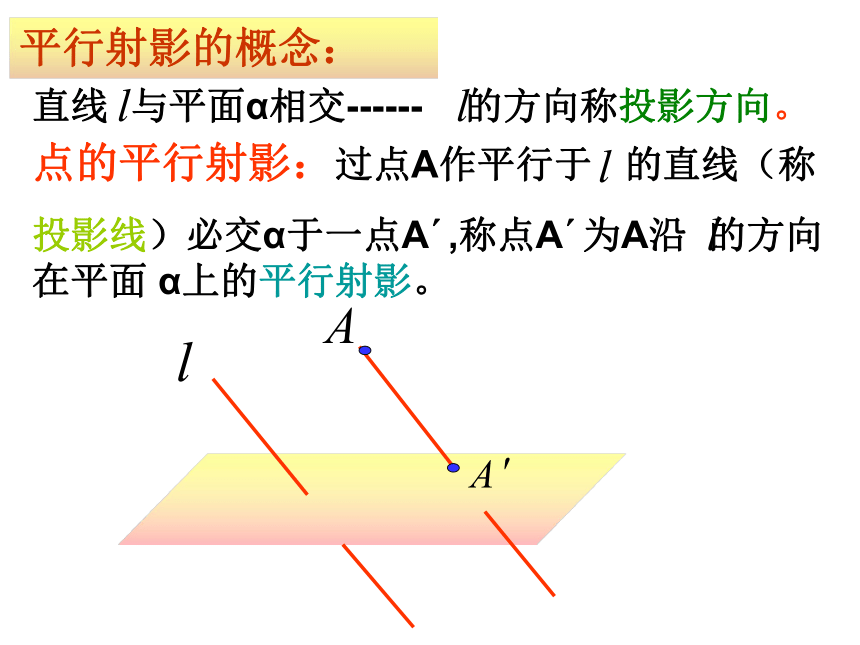
什么图形?思考:平行射影的概念:直线 与平面α相交------ 的方向称投影方向。点的平行射影:过点A作平行于 的直线(称
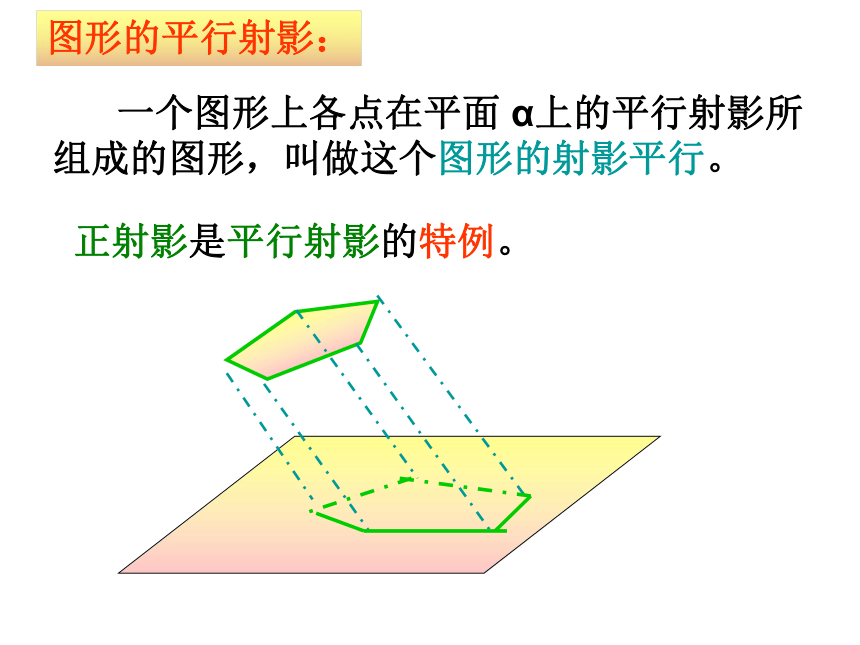
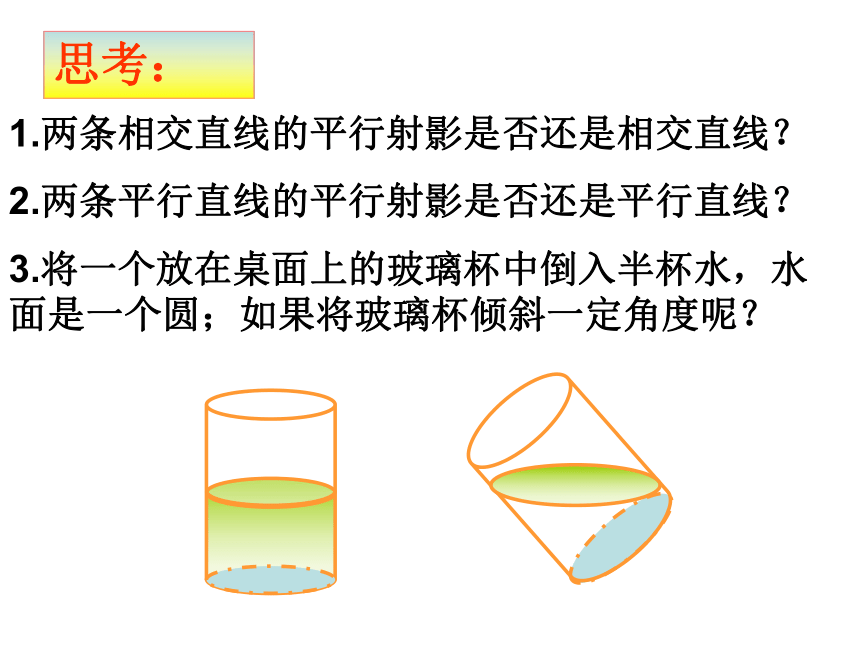
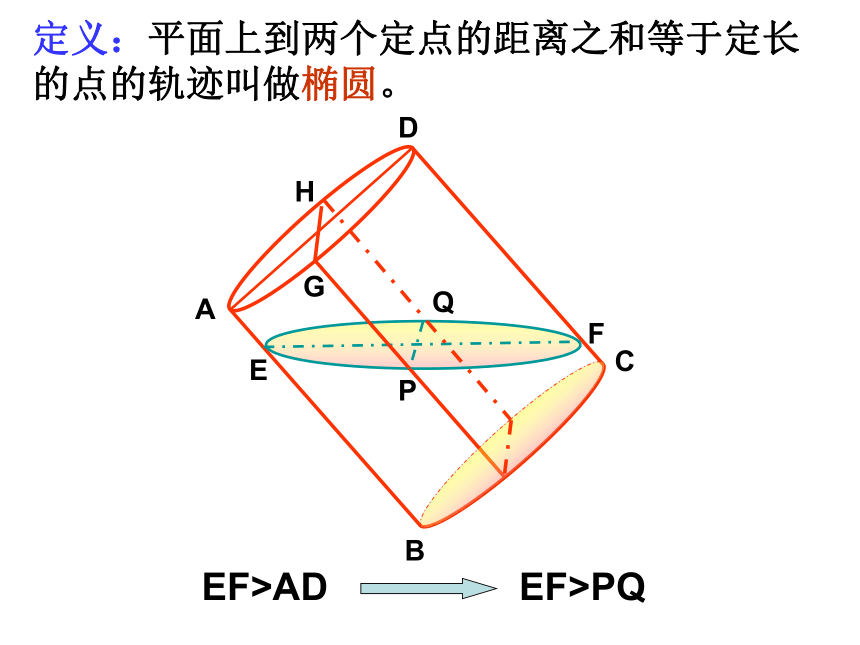
投影线)必交α于一点A′,称点A′为A沿 的方向在平面 α上的平行射影。 一个图形上各点在平面 α上的平行射影所组成的图形,叫做这个图形的射影平行。正射影是平行射影的特例。图形的平行射影:思考:1.两条相交直线的平行射影是否还是相交直线?2.两条平行直线的平行射影是否还是平行直线?3.将一个放在桌面上的玻璃杯中倒入半杯水,水面是一个圆;如果将玻璃杯倾斜一定角度呢?EF>AD EF>PQ定义:平面上到两个定点的距离之和等于定长的点的轨迹叫做椭圆。用一个平面去截一个圆柱,
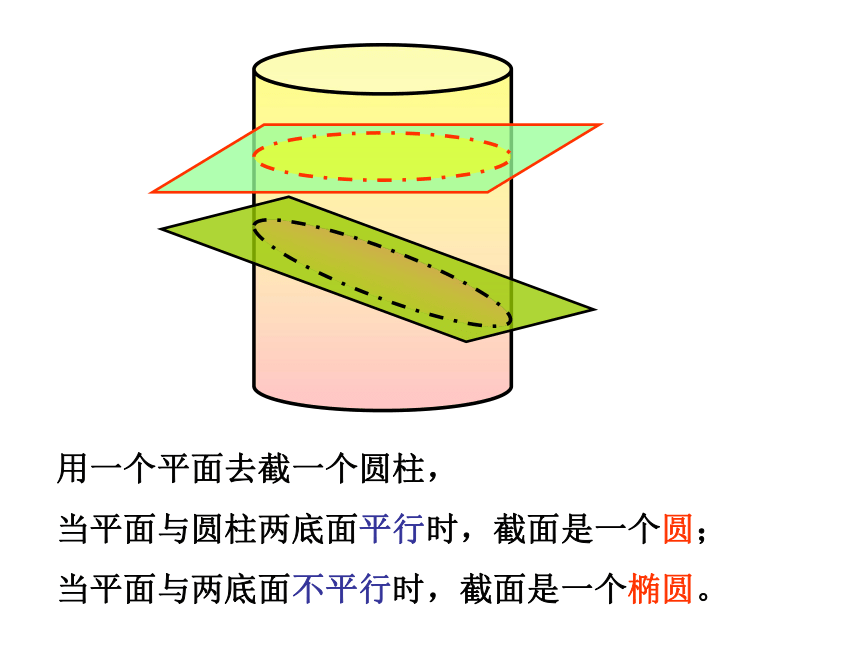
当平面与圆柱两底面平行时,截面是一个圆;
当平面与两底面不平行时,截面是一个椭圆。二.平面与圆柱面的截线二。平面与圆柱面的截线探究: 如图,AB,CD是两个等
圆的直径,AB//CD,均与
两圆相切。作公切线EF,
切点分别为 交BA,DC
的延长线与E,F,交AD于
,交BC于 ,设EF
与BC,CD的交角分别
为φ,θ。拓展到空间Dandlin双球(丹迪林)定理1.圆柱形物体的斜截口是椭圆.APBC椭圆的准线: , 离心率:三.平面与圆锥面的截线底面为圆截痕为圆截面截面与圆锥的高垂直時截痕为圆圆锥高VH截痕之一:椭圆 如果用一个平面去截一个正圆锥(两边可以无限延伸),而且这个平面不通过圆锥的顶点,会出现三种情况:底面为圆正圆锥面截面截痕为椭圆截面与圆锥面的高不垂直時截痕可能为一个椭圆正圆锥高截痕之二:抛物线底为圆正圆锥面截面圆锥高VH截痕为抛物线截面与圆锥的母线平行時其截面为抛物线圆锥母线截痕之三:双曲线底面圆正圆锥面截痕为双曲线截面截痕为双曲线定理2 在空中,取直线 为轴,直线 与 相交于O点,夹角为 , 围绕 旋转得到以O为顶点, 为母线的圆锥面。任取平面π,若它与轴 的交角为 (当 π与 平行时,记 =0),则(1)β>α,平面π与圆锥的交线为椭圆;
(2) β=α,平面π与圆锥的交线为抛物线;
(3)β<α,平面π与圆锥的交线为双曲线。抛物线焦点的产生圆锥面截面含切点圆的平面
(切点面)截面与切点面交线
(准线)拋物线焦点的产生由截面截出的拋物线对称轴內切球面球面与圆锥面相切(切点圆)球的切点
(焦点)椭圆焦点的产生圆锥面截面內切大球面內切小球面大球的切点 (焦点)小球的切点 (焦点)球面与锥面相切球面与锥面相切由截面截出的椭圆椭圆焦点的产生双曲线焦点的产生
圆锥曲线性质的探讨一.平行射影复习回顾点在直线上的正射影 线段在直线上的正射影 点在平面上的正射影 拓展延伸AA′图形在平面上的正射影 一个圆所在的平面β与平面α平行时,该圆在α上的正射影是什么图形? 当β与α不平行时,圆在α上的正射影是什么图形? 如果 β与α垂直,圆在α上的正射影又是
什么图形?思考:平行射影的概念:直线 与平面α相交------ 的方向称投影方向。点的平行射影:过点A作平行于 的直线(称
投影线)必交α于一点A′,称点A′为A沿 的方向在平面 α上的平行射影。 一个图形上各点在平面 α上的平行射影所组成的图形,叫做这个图形的射影平行。正射影是平行射影的特例。图形的平行射影:思考:1.两条相交直线的平行射影是否还是相交直线?2.两条平行直线的平行射影是否还是平行直线?3.将一个放在桌面上的玻璃杯中倒入半杯水,水面是一个圆;如果将玻璃杯倾斜一定角度呢?EF>AD EF>PQ定义:平面上到两个定点的距离之和等于定长的点的轨迹叫做椭圆。用一个平面去截一个圆柱,
当平面与圆柱两底面平行时,截面是一个圆;
当平面与两底面不平行时,截面是一个椭圆。二.平面与圆柱面的截线二。平面与圆柱面的截线探究: 如图,AB,CD是两个等
圆的直径,AB//CD,均与
两圆相切。作公切线EF,
切点分别为 交BA,DC
的延长线与E,F,交AD于
,交BC于 ,设EF
与BC,CD的交角分别
为φ,θ。拓展到空间Dandlin双球(丹迪林)定理1.圆柱形物体的斜截口是椭圆.APBC椭圆的准线: , 离心率:三.平面与圆锥面的截线底面为圆截痕为圆截面截面与圆锥的高垂直時截痕为圆圆锥高VH截痕之一:椭圆 如果用一个平面去截一个正圆锥(两边可以无限延伸),而且这个平面不通过圆锥的顶点,会出现三种情况:底面为圆正圆锥面截面截痕为椭圆截面与圆锥面的高不垂直時截痕可能为一个椭圆正圆锥高截痕之二:抛物线底为圆正圆锥面截面圆锥高VH截痕为抛物线截面与圆锥的母线平行時其截面为抛物线圆锥母线截痕之三:双曲线底面圆正圆锥面截痕为双曲线截面截痕为双曲线定理2 在空中,取直线 为轴,直线 与 相交于O点,夹角为 , 围绕 旋转得到以O为顶点, 为母线的圆锥面。任取平面π,若它与轴 的交角为 (当 π与 平行时,记 =0),则(1)β>α,平面π与圆锥的交线为椭圆;
(2) β=α,平面π与圆锥的交线为抛物线;
(3)β<α,平面π与圆锥的交线为双曲线。抛物线焦点的产生圆锥面截面含切点圆的平面
(切点面)截面与切点面交线
(准线)拋物线焦点的产生由截面截出的拋物线对称轴內切球面球面与圆锥面相切(切点圆)球的切点
(焦点)椭圆焦点的产生圆锥面截面內切大球面內切小球面大球的切点 (焦点)小球的切点 (焦点)球面与锥面相切球面与锥面相切由截面截出的椭圆椭圆焦点的产生双曲线焦点的产生
