正方形的判定
图片预览


文档简介
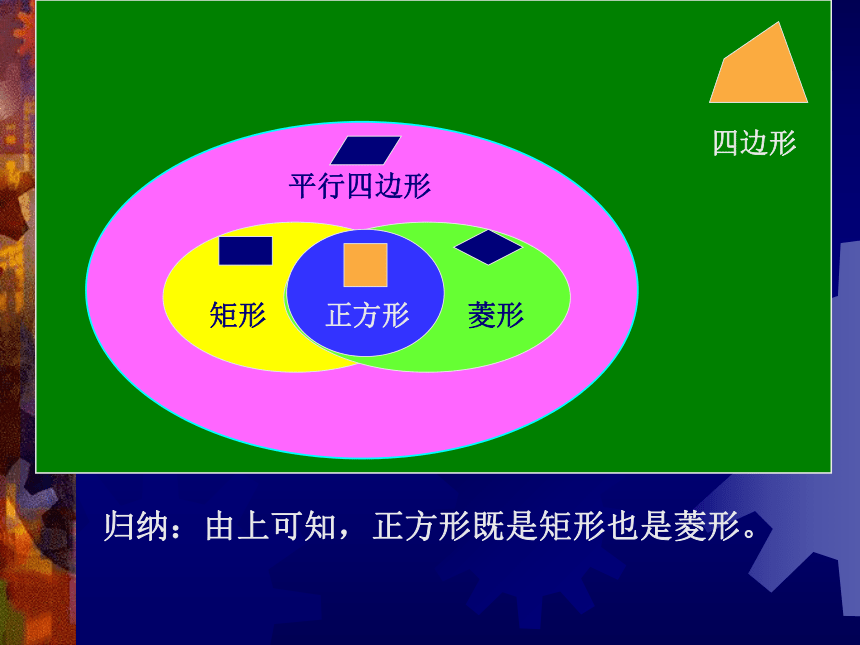
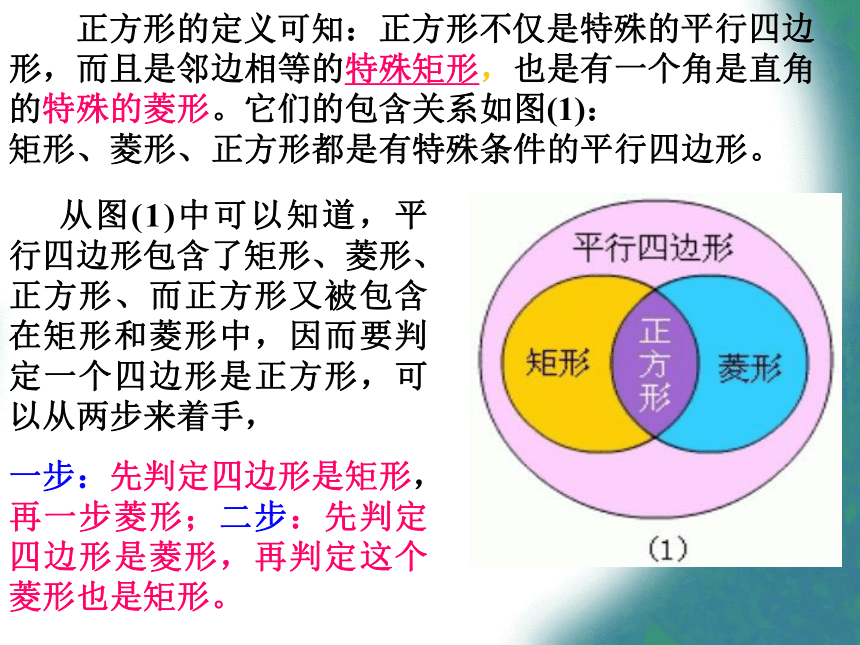
课件21张PPT。正方形的判定吼滩中学 八(5)班 教师:陈攀 5月11日正方形的定义定义一:有一个角是直角的菱形是正方形.定义二:有一组邻边相等的矩形是正方形.正方形的判定判定一:有一个角是直角的菱形是正方形.判定二:有一组邻边相等的矩形是正方形.研究正方形的判定:(1)边:四边都相等;(2)角:四角都是直角;的四边形是正方形(3)对角线:相等;互相垂直平分;判定方法判定方法的四边形是正方形矩形菱形正方形平行四边形四边形归纳:由上可知,正方形既是矩形也是菱形。 正方形的定义可知:正方形不仅是特殊的平行四边形,而且是邻边相等的特殊矩形,也是有一个角是直角的特殊的菱形。它们的包含关系如图(1):
矩形、菱形、正方形都是有特殊条件的平行四边形。 从图(1)中可以知道,平行四边形包含了矩形、菱形、正方形、而正方形又被包含在矩形和菱形中,因而要判定一个四边形是正方形,可以从两步来着手,
一步:先判定四边形是矩形,再一步菱形;二步:先判定四边形是菱形,再判定这个菱形也是矩形。
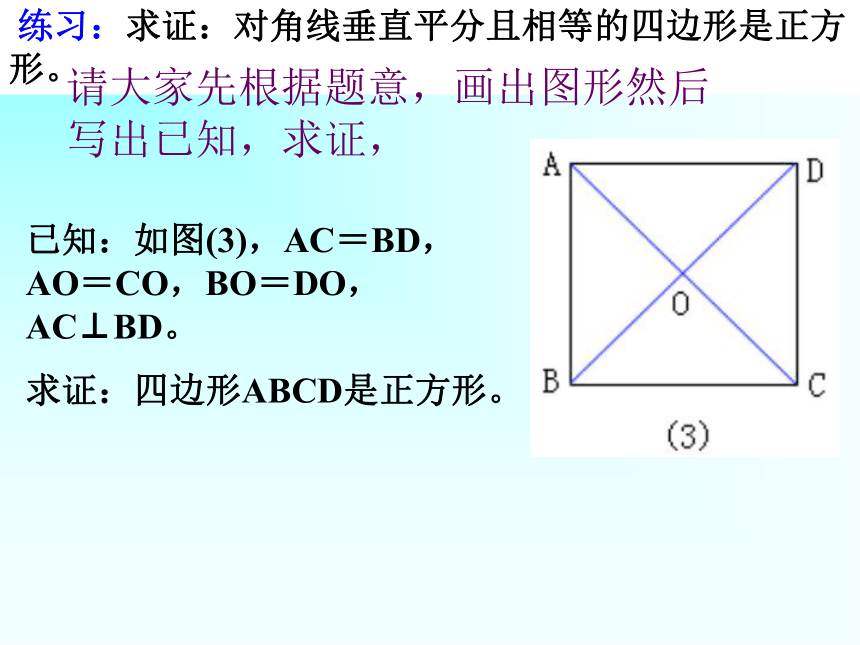
练习:求证:对角线垂直平分且相等的四边形是正方形。 已知:如图(3),AC=BD,AO=CO,BO=DO,AC⊥BD。
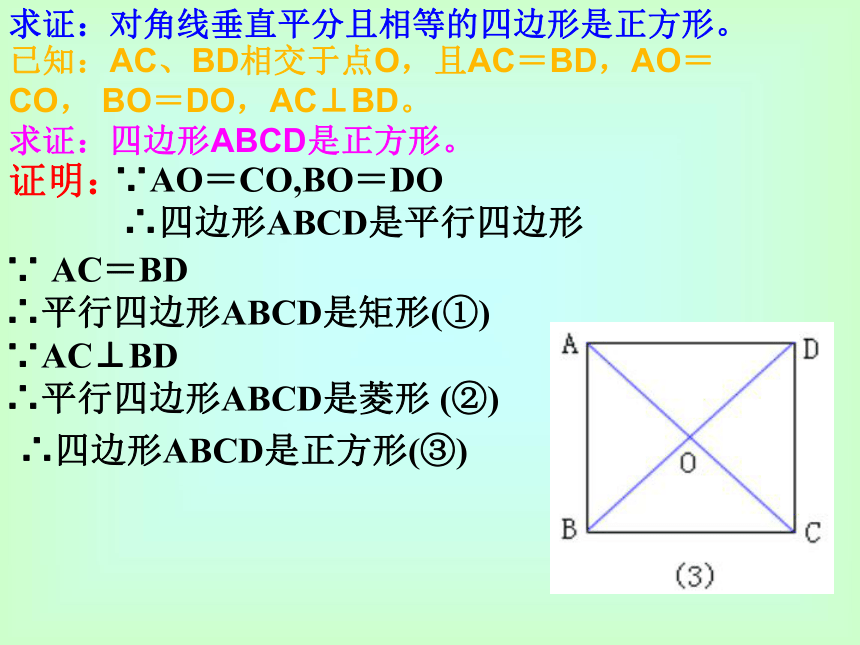
求证:四边形ABCD是正方形。 请大家先根据题意,画出图形然后写出已知,求证,求证:对角线垂直平分且相等的四边形是正方形。 已知:AC、BD相交于点O,且AC=BD,AO=CO, BO=DO,AC⊥BD。 求证:四边形ABCD是正方形。
证明:
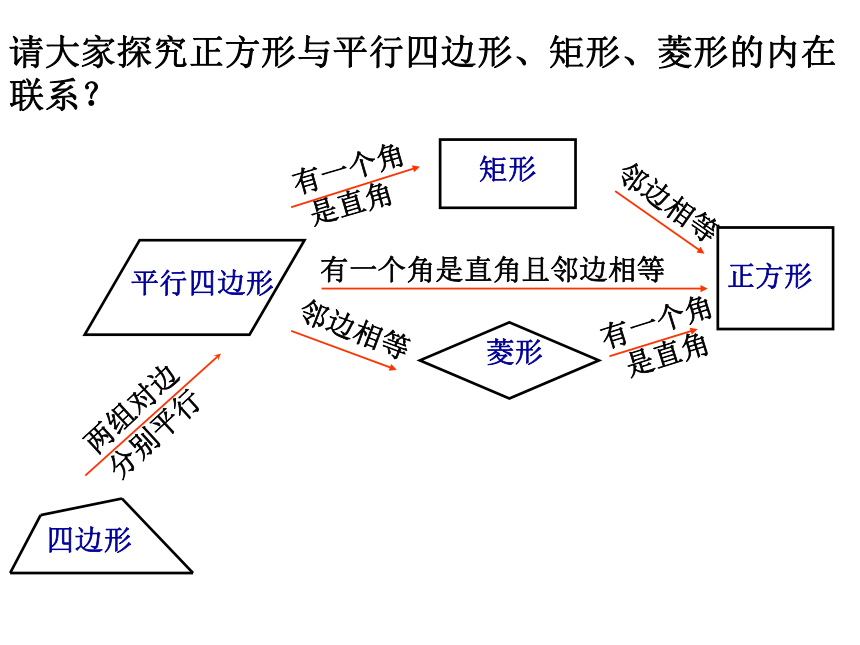
∵AO=CO,BO=DO ∴四边形ABCD是平行四边形∵ AC=BD ∴平行四边形ABCD是矩形(①) ∵AC⊥BD ∴平行四边形ABCD是菱形 (②)∴四边形ABCD是正方形(③) 四边形请大家探究正方形与平行四边形、矩形、菱形的内在联系?掌握正方形的判定的方法。 正方形中,课本上没有给出明显的判定定理,它只告诉我们,要判定一个四边形是正方形,分两个步骤:根据内在联系,得出平行四边形它包含了矩形、菱形、正方形;而正方形又包含在矩形和 菱形中。 第一步:先判定四边形是矩形,再 判定这个矩形又是菱形;
第二步:先判定四边形是菱形,再判定这个菱形又是矩形,即可判定它是正方形。
1. 把一个长方形纸片如图那样折一下,就可以裁出正方形纸片,为什么?
2. 判断下列命题是否正确.
(1) 对角线互相垂直且相等的平行四边形是正方形.
(2) 对角线互相垂直的矩形是正方形.
(3) 对角线相等的菱形是正方形.
(4) 对角线互相垂直平分且相等的四边形是正方形. 巩固练习:判断下列命题是否正确,不是正方形的补充什么条件能让它成为正方形?四个角都相等的四边形是正方形; ( )
四条边都相等的四边形是正方形; ( )
对角线相等的菱形是正方形; ( )
对角线互相垂直的矩形是正方形; ( )
对角线垂直且相等的四边形是正方形; ( )
四边相等,有一个角是直角的四边形
是正方形. ( )√√√××× 1.四个内角都相等的四边形一定是: A.正方形 B.菱形 C.矩形 D.平行四边形 2.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正 方形的是: A.AO=BO=CO=DO,AC⊥BD B.AD∥BC ∠A=∠C C.AO=CO BO=DO AB=BC D.AC=BD 3 .四个内角都相等,四条边也都相等的四边形一定是:A.正方形 B.菱形 C.矩形 D.平行四边形 练习:如图已知四边形ABCD为正方形,四边形AEFC为菱形,EH⊥AC,垂足为H。试证明FC=2EH。4、证明题:已知:如图(2),点A‘、B’、C‘、D’分别是正方形ABCD 的边AB、BC、CD、DA的中点,求证:四边形A'B'C'D'是正方形。 分析(1)你能证明四边形是矩形吗?
(2)你能证明四边形是菱形吗?
(3)你能证明四边形是正方形吗?? 证明:∵四边形ABCD是正方形 ∴AD=AB=BC, ∠A=∠B=90° 又∵D’,A ’,B ’是 DA 、 AB、BC的中点 ∴AD’=AA’=A’B=BB’ ∴∠1=∠2=∠3=∠4=45°
∴∠D’A’B’=180°-∠1-∠3=90°同理:∠A’B’C’=90° ∠B’C’D’=90° ∴四边形A’B’C’D’是矩形( ① )在△D’AA’和△A’BB’中
AD’=AB’,∠A=∠B,AA’=BB’∴△D‘AA’≌△A‘BB’(SAS) ∴A‘D’=A‘B’ ∴四边形A‘B’C‘D’是正方形( ② )已知:在△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC, DF⊥AC,垂足分别为E、F. 求证: 四边形CFDE是正方形. ∵ CD平分∠ACB,
DE⊥BC, DF⊥AC,
∴ DE=DF(①).
又∵ ∠DEC=∠ECF=∠CFD=90°,
∴ 四边形CFDE是矩形(②),
∴ 四边形CFDE是正方形(③).应用如图,在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D。DE⊥AC,DF⊥AB。求证:四边形CEDF为正方形ABCDEFG证明:过点D作DG⊥AB,垂足为G
∵AD是∠CAB的平分线
DE⊥AC,DG⊥AB
∴ DE=DG同理:DG=DF∴ED=DF ∵ DE⊥AC,DF⊥AB
∴∠DEC= ∠DFC=90 °
又∵ ∠C=90 ° ∴四边形ADFC是矩形
∴四边形ADFC是正方形
已知: 如图,点A′、 B′、 C′、 D′分别是正方形ABCD四条边上的点,并且AA′=BB′=CC′=DD′.求证: 四边形A′B′C′D′是正方形.
如图,在正方形ABCD中,CE⊥DF.求证: CE=DF. 11.在正方形ABCD中,
P为BC边上一点,
Q为CD边上一点,
如果PQ=BP+DQ,
求∠PAQ的度数.三、特殊四边形的常用判定方法平行
四边形(1)两组对边分别平行;(2)两组对边分别相等;(4)两条对角线互相平分;(3)两组对角矩 形(1)有三个角是直角;(2)是平行四边形,并且有一个角是直角;(3)是平行四边形,并且两条对角线相等。 菱 形(1)四条边都相等;(2)是平行四边形,并且有一组邻边相等;(3)是平行四边形,并且两条对角线互相垂直。正方形(1)是矩形,并且有一组邻边相等;(2)是菱形,并且有一个角是直角。分别相等;
一步:先判定四边形是矩形,再一步菱形;二步:先判定四边形是菱形,再判定这个菱形也是矩形。
练习:求证:对角线垂直平分且相等的四边形是正方形。 已知:如图(3),AC=BD,AO=CO,BO=DO,AC⊥BD。
求证:四边形ABCD是正方形。 请大家先根据题意,画出图形然后写出已知,求证,求证:对角线垂直平分且相等的四边形是正方形。 已知:AC、BD相交于点O,且AC=BD,AO=CO, BO=DO,AC⊥BD。 求证:四边形ABCD是正方形。
证明:
∵AO=CO,BO=DO ∴四边形ABCD是平行四边形∵ AC=BD ∴平行四边形ABCD是矩形(①) ∵AC⊥BD ∴平行四边形ABCD是菱形 (②)∴四边形ABCD是正方形(③) 四边形请大家探究正方形与平行四边形、矩形、菱形的内在联系?掌握正方形的判定的方法。 正方形中,课本上没有给出明显的判定定理,它只告诉我们,要判定一个四边形是正方形,分两个步骤:根据内在联系,得出平行四边形它包含了矩形、菱形、正方形;而正方形又包含在矩形和 菱形中。 第一步:先判定四边形是矩形,再 判定这个矩形又是菱形;
第二步:先判定四边形是菱形,再判定这个菱形又是矩形,即可判定它是正方形。
1. 把一个长方形纸片如图那样折一下,就可以裁出正方形纸片,为什么?
2. 判断下列命题是否正确.
(1) 对角线互相垂直且相等的平行四边形是正方形.
(2) 对角线互相垂直的矩形是正方形.
(3) 对角线相等的菱形是正方形.
(4) 对角线互相垂直平分且相等的四边形是正方形. 巩固练习:判断下列命题是否正确,不是正方形的补充什么条件能让它成为正方形?四个角都相等的四边形是正方形; ( )
四条边都相等的四边形是正方形; ( )
对角线相等的菱形是正方形; ( )
对角线互相垂直的矩形是正方形; ( )
对角线垂直且相等的四边形是正方形; ( )
四边相等,有一个角是直角的四边形
是正方形. ( )√√√××× 1.四个内角都相等的四边形一定是: A.正方形 B.菱形 C.矩形 D.平行四边形 2.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正 方形的是: A.AO=BO=CO=DO,AC⊥BD B.AD∥BC ∠A=∠C C.AO=CO BO=DO AB=BC D.AC=BD 3 .四个内角都相等,四条边也都相等的四边形一定是:A.正方形 B.菱形 C.矩形 D.平行四边形 练习:如图已知四边形ABCD为正方形,四边形AEFC为菱形,EH⊥AC,垂足为H。试证明FC=2EH。4、证明题:已知:如图(2),点A‘、B’、C‘、D’分别是正方形ABCD 的边AB、BC、CD、DA的中点,求证:四边形A'B'C'D'是正方形。 分析(1)你能证明四边形是矩形吗?
(2)你能证明四边形是菱形吗?
(3)你能证明四边形是正方形吗?? 证明:∵四边形ABCD是正方形 ∴AD=AB=BC, ∠A=∠B=90° 又∵D’,A ’,B ’是 DA 、 AB、BC的中点 ∴AD’=AA’=A’B=BB’ ∴∠1=∠2=∠3=∠4=45°
∴∠D’A’B’=180°-∠1-∠3=90°同理:∠A’B’C’=90° ∠B’C’D’=90° ∴四边形A’B’C’D’是矩形( ① )在△D’AA’和△A’BB’中
AD’=AB’,∠A=∠B,AA’=BB’∴△D‘AA’≌△A‘BB’(SAS) ∴A‘D’=A‘B’ ∴四边形A‘B’C‘D’是正方形( ② )已知:在△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC, DF⊥AC,垂足分别为E、F. 求证: 四边形CFDE是正方形. ∵ CD平分∠ACB,
DE⊥BC, DF⊥AC,
∴ DE=DF(①).
又∵ ∠DEC=∠ECF=∠CFD=90°,
∴ 四边形CFDE是矩形(②),
∴ 四边形CFDE是正方形(③).应用如图,在直角三角形中,∠C=90°,∠A、∠B的平分线交于点D。DE⊥AC,DF⊥AB。求证:四边形CEDF为正方形ABCDEFG证明:过点D作DG⊥AB,垂足为G
∵AD是∠CAB的平分线
DE⊥AC,DG⊥AB
∴ DE=DG同理:DG=DF∴ED=DF ∵ DE⊥AC,DF⊥AB
∴∠DEC= ∠DFC=90 °
又∵ ∠C=90 ° ∴四边形ADFC是矩形
∴四边形ADFC是正方形
已知: 如图,点A′、 B′、 C′、 D′分别是正方形ABCD四条边上的点,并且AA′=BB′=CC′=DD′.求证: 四边形A′B′C′D′是正方形.
如图,在正方形ABCD中,CE⊥DF.求证: CE=DF. 11.在正方形ABCD中,
P为BC边上一点,
Q为CD边上一点,
如果PQ=BP+DQ,
求∠PAQ的度数.三、特殊四边形的常用判定方法平行
四边形(1)两组对边分别平行;(2)两组对边分别相等;(4)两条对角线互相平分;(3)两组对角矩 形(1)有三个角是直角;(2)是平行四边形,并且有一个角是直角;(3)是平行四边形,并且两条对角线相等。 菱 形(1)四条边都相等;(2)是平行四边形,并且有一组邻边相等;(3)是平行四边形,并且两条对角线互相垂直。正方形(1)是矩形,并且有一组邻边相等;(2)是菱形,并且有一个角是直角。分别相等;
