图形旋转变换

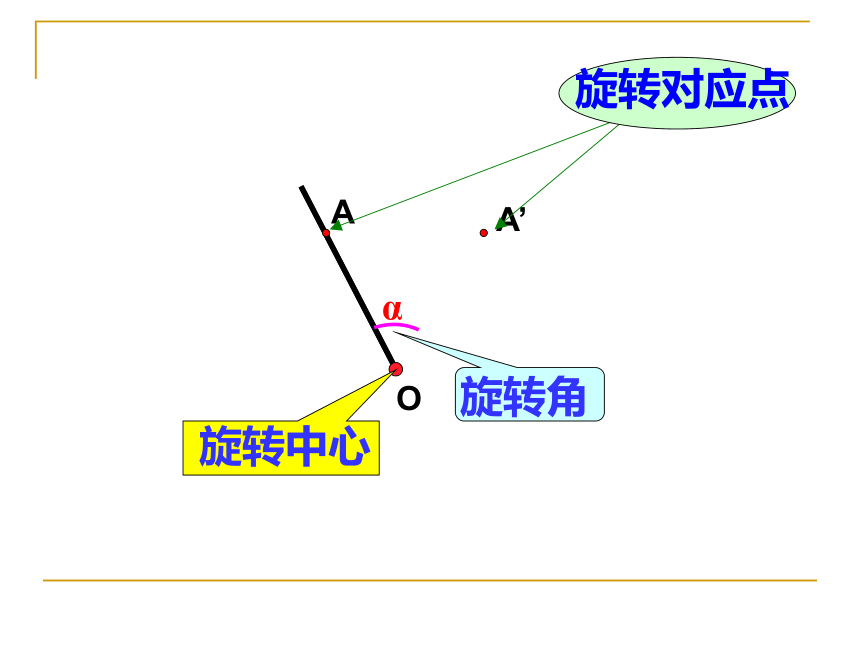
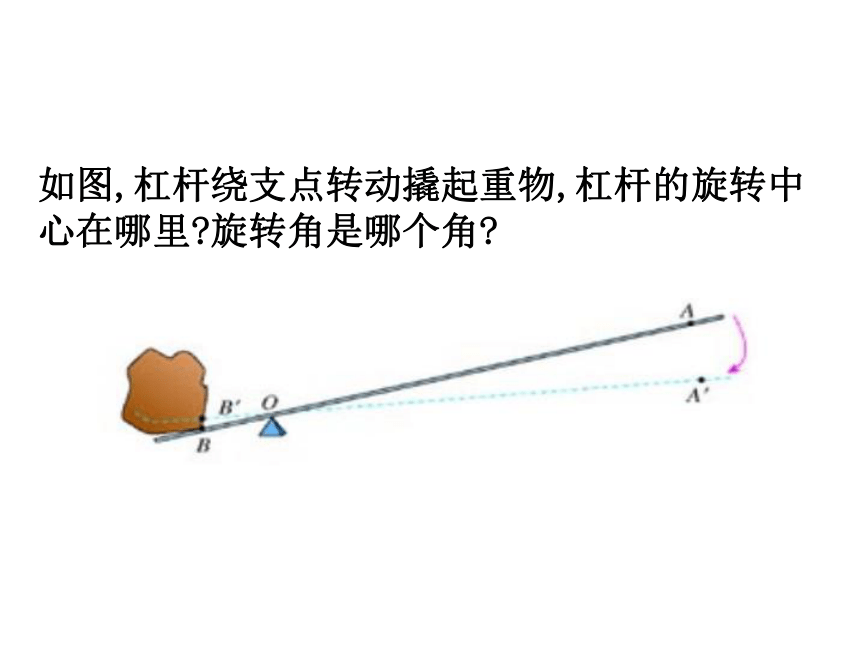
课件13张PPT。图形的旋转旋转角旋转中心OαAA’PP’如图,杠杆绕支点转动撬起重物,杠杆的旋转中 心在哪里?旋转角是哪个角? 如图,△ABC绕点O按顺时针方向旋转到△A'B'C'的位置 .ABCOA/B/C/3. ∠AOA’=∠BOB’ =∠COC’2. AO=A’O
BO=B’O
CO=C’O（2）经过旋转，
点A、B分别移动
到什么位置？探究（1）旋转中心是什么？1.△ABC≌△A'B'C'线段OB的对应线段是线段______ ∠A的对应角是______ 线段AB的对应线段是线段______ ∠B的对应角是______ 旋转中心是点______ ∠BOB ′的度数是 ______ 点B的对应点是点_____ 1.如图，是△AOB绕点O按逆时针方向旋转450所得的.B′0B′A’B’∠A′∠B′O450练习2.如图，E是正方形ABCD中CD边上任意一点，以点A为中心，把△ADE顺时针旋转90°，画出旋转后的图形(简述作图方法).解：∵点A是旋转中心，∴它的对应点是它本身.
正方形ABCD中，AD=AB，∠DAB=90°，所以旋转后点D与点B重合.
设点E的对应点为点E'.
∵旋转后的图形与旋转前的图形全等
∴∠ABE'=∠ADE=90°，BE'=DE
因此在CB的延长线上取点E'，使BE'=DE
则△ABE'为旋转后的图形3.如图，P是等边三角形ABC内的一点，若将△PAC逆时针旋转到达△P'AB的位置.(1)旋转中心是点_____,
旋转度数是 ,
线段CP的对应边是线段_ __； (4)若PA=6，PB=8，PC=10.求点P与点P'之间的距离及∠APB的度数.(3)若连结PP',则△APP'是 三角形，简单说明理由.(2)如果M是AC的中点，那么经过上述旋转后，点M转到了什么位置？
A60°BP’等边4.如图，P是等边三角形ABC内的一点，若PA=6，PB=8，PC=10. ∠APB的度数.解：以点A为旋转中心，把△ACP逆时针旋转60°，得到△ABP’ 连接PP'
∵∠PAP'=60° ，AP=AP'
∴△APP’是等边三角形
∴PP'=PA=6 ∠APP'=60°
在△BPP'中，BP2+PP'2=82+62=100
BP'2=102=100
∴BP2+PP'2=BP'2
∴∠BPP'=90°
∴∠APB= ∠APP'+∠BPP'=60°+90°=150°则△ABP’≌△ACP
∴AP'=PA=6 BP'=PC=10思考：下图是由正方形ABCD旋转而成.(1) 旋转中心是__________

(2) 旋转的角度是_________点A450(3) 若正方形的边长是1，则C’D=_________C'D'B'BACD课堂回顾：
这节课，主要学习了什么？1.旋转的概念 2.旋转的性质