安徽省优秀教师数学课件展示:等比数列前n项和(贵池中学)
文档属性
| 名称 | 安徽省优秀教师数学课件展示:等比数列前n项和(贵池中学) |

|
|
| 格式 | rar | ||
| 文件大小 | 956.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-06-21 00:00:00 | ||
图片预览






文档简介
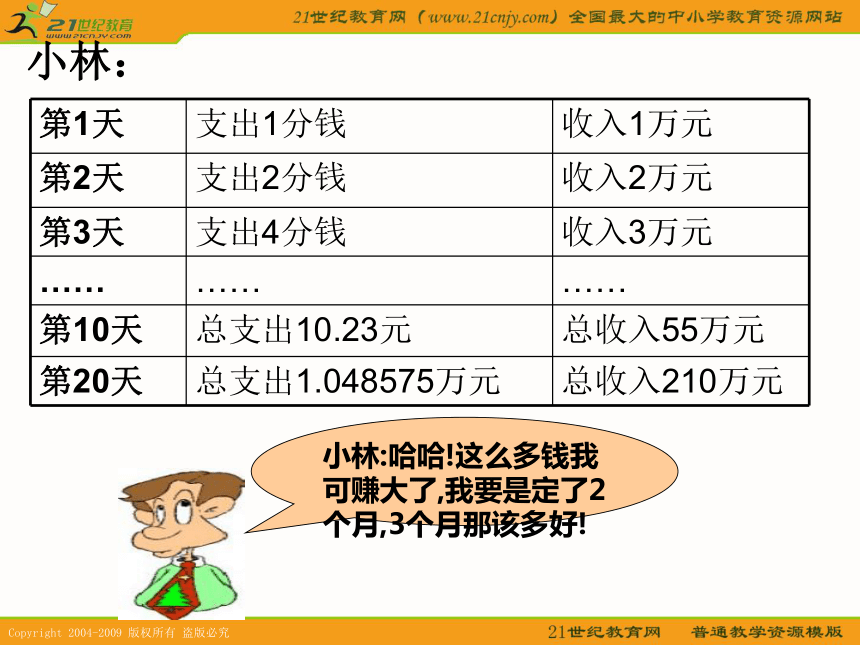
课件16张PPT。小林:我第一天还1分钱,以后每天还的钱是前一天的2倍一、问题探究引入小林:哈哈!这么多钱我可赚大了,我要是定了2个月,3个月那该多好!小林:设30天后,小林得到的钱数为L30(万元),小明得到的钱数为M30(分),则根据合同能列出式子L30=1+2+3+…….+30=(1+30)×30/2
=30×1+30×(30-1)/2=465 (万元)M30=1+2+22+…….+229 ①思路一 M30=1+2+22+…….+229
M30=1+2(1+2+22+……+228)
M30=1+2(M30-229)
M30- 2M30=1-230
M30=230-1思路二 M30=1+2+22+…….+229 ②
2M30=2+22+23+….+229+230 ③
③-②得 M30=230-1M30 =230-1
=1073741823(分)=1073.741823(万元)设等比数列{an}的前n项和
Sn=a1+a2+a3+……+an 即说明:这种求和方法称为错位相减法二、推进新课Sn = a1 + a1q + a1q2 +…+a1qn-2 + a1qn-1 qSn = a1q + a1q2 + a1q3 + ….+ a1qn-1+ a1qn 两式相减有 ( 1 – q )Sn = a1 – a1 q n 当q=1时,思考:
(1-q)可以直接除过去吗? ( 1 – q )Sn = a1 – a1 q n 等比数列前n项和求和公式 na1 (q=1) (q≠1)等比数列前n项和公式的其他推导方法探究一:由等比数列定义,有:再由合比定理得:[合作探究]即:从而有 ( 1 – q )Sn = a1 – a1 q n [合作探究]从而有 ( 1 – q )Sn = a1 – a1 q n 三、例题剖析:例1.
(1)已知等比数列{an}中, a1=2,q=3,求S3
(2)求等比数列1,1/2 ,1/4 ,1/8 ,…的前10项和 巩固练习1:
求下列等比数列{an}前n项和
a1=1,q=3,n=5
(2) a1=6,q=2, an=192
(3) a1=1,q=χ, n=5
巩固练习2:
P31练习1-2例2.五洲电扇厂去年实现利税300万元,计划在以后5年中每年比上年利税增长10%,问从今年起第5年的利税是多少?这5年的总利税是多少?(结果精确到万元)分析提问:根据题意,从中发现怎样的等比关系?今年起第5年的利税为等比数列的第几项?这5年的总利税是哪几项和? 四、课堂小结:1、等比数列的前n项和公式的推导
第一种方法称之为错位相减法
第二种依赖的是定义特征及等比性质进行推导,
第三种则是借助和式的代数特征进行恒等变形而得,2、等比数列的前n项和公式的应用
由 Sn .an ,q , a1 , n 知三而可求二 .
另外应注意公式有两个形式在应用中应恰当选用
对于含有字母的等比数列应注意考虑其公比是否为1。 五、布置作业 课本P34 A组7、8、9题
谢谢大家!
=30×1+30×(30-1)/2=465 (万元)M30=1+2+22+…….+229 ①思路一 M30=1+2+22+…….+229
M30=1+2(1+2+22+……+228)
M30=1+2(M30-229)
M30- 2M30=1-230
M30=230-1思路二 M30=1+2+22+…….+229 ②
2M30=2+22+23+….+229+230 ③
③-②得 M30=230-1M30 =230-1
=1073741823(分)=1073.741823(万元)设等比数列{an}的前n项和
Sn=a1+a2+a3+……+an 即说明:这种求和方法称为错位相减法二、推进新课Sn = a1 + a1q + a1q2 +…+a1qn-2 + a1qn-1 qSn = a1q + a1q2 + a1q3 + ….+ a1qn-1+ a1qn 两式相减有 ( 1 – q )Sn = a1 – a1 q n 当q=1时,思考:
(1-q)可以直接除过去吗? ( 1 – q )Sn = a1 – a1 q n 等比数列前n项和求和公式 na1 (q=1) (q≠1)等比数列前n项和公式的其他推导方法探究一:由等比数列定义,有:再由合比定理得:[合作探究]即:从而有 ( 1 – q )Sn = a1 – a1 q n [合作探究]从而有 ( 1 – q )Sn = a1 – a1 q n 三、例题剖析:例1.
(1)已知等比数列{an}中, a1=2,q=3,求S3
(2)求等比数列1,1/2 ,1/4 ,1/8 ,…的前10项和 巩固练习1:
求下列等比数列{an}前n项和
a1=1,q=3,n=5
(2) a1=6,q=2, an=192
(3) a1=1,q=χ, n=5
巩固练习2:
P31练习1-2例2.五洲电扇厂去年实现利税300万元,计划在以后5年中每年比上年利税增长10%,问从今年起第5年的利税是多少?这5年的总利税是多少?(结果精确到万元)分析提问:根据题意,从中发现怎样的等比关系?今年起第5年的利税为等比数列的第几项?这5年的总利税是哪几项和? 四、课堂小结:1、等比数列的前n项和公式的推导
第一种方法称之为错位相减法
第二种依赖的是定义特征及等比性质进行推导,
第三种则是借助和式的代数特征进行恒等变形而得,2、等比数列的前n项和公式的应用
由 Sn .an ,q , a1 , n 知三而可求二 .
另外应注意公式有两个形式在应用中应恰当选用
对于含有字母的等比数列应注意考虑其公比是否为1。 五、布置作业 课本P34 A组7、8、9题
谢谢大家!
