4.2.1直线与圆的位置关系学案
文档属性
| 名称 | 4.2.1直线与圆的位置关系学案 |
|
|
| 格式 | rar | ||
| 文件大小 | 21.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-06-23 00:00:00 | ||
图片预览

文档简介
4.2.1直线与圆的位置关系学案
复习引入
1. 直线的方程:
2. 圆的标准方程 圆心 半径
3. 圆的一般方程 圆心 半径
知识探究
思考1:在平面几何中,直线与圆的位置关系有几种?
思考2:类比点与圆的位置关系的判断,我们怎样判断直线与圆的位置关系?
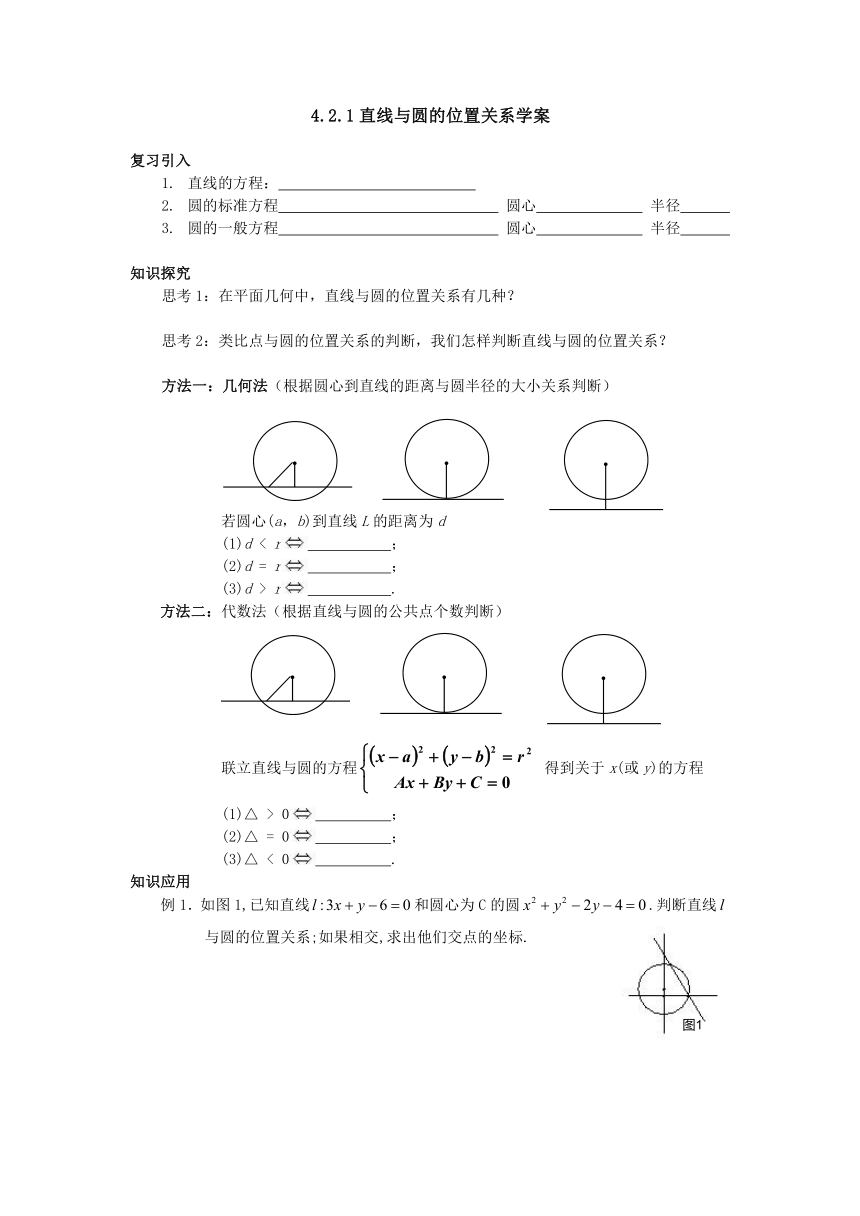
方法一:几何法(根据圆心到直线的距离与圆半径的大小关系判断)
若圆心(a,b)到直线L的距离为d
(1)d < r ;
(2)d = r ;
(3)d > r .
方法二:代数法(根据直线与圆的公共点个数判断)
联立直线与圆的方程 得到关于x(或y)的方程
(1)△ > 0 ;
(2)△ = 0 ;
(3)△ < 0 .
知识应用
例1.如图1,已知直线和圆心为C的圆.判断直线 与圆的位置关系;如果相交,求出他们交点的坐标.
变式训练:判断直线L:与圆O:的位置关系.
例2.已知过点M(-3,-3)的直线被圆所截得的弦长为,求
的方程。
变式训练:直线y = 2x + b与圆相交于A、B两点,则弦AB的中点M的轨迹方程是 。
例4.已知点是圆上一点,求过点P的圆C的切线方程。
巩固练习
1.直线4x – 3y = 0和圆 x2 + y2 – 18x – 45 = 0的位置关系是 ( )
A.相交 B.相离 C.相切 D.不确定.
2.直线 与圆x2 + y2 - 2 x - 2 = 0相切,则实数m等于 ( )
A.或 B.或 C.或 D.或
3.直线l: x - y + 4 = 0圆C: (x-1)2 + (y - 1)2 = 2,则C上各点到l距离最小值为( )
A. B. C.3 D.
4.已知圆方程,直线,当为何值时,圆与直线相交、相切、相离.
5.过点P(1,-1)的直线l与圆M:
(1)当直线和圆相切时,求切线方程和切线长;
(2)若直线的斜率为2,求直线被圆截得的弦AB的长;
(3)若圆的方程加上条件x≥3,直线与圆有且只有一个交点,求直线的斜率的取值范围.
复习引入
1. 直线的方程:
2. 圆的标准方程 圆心 半径
3. 圆的一般方程 圆心 半径
知识探究
思考1:在平面几何中,直线与圆的位置关系有几种?
思考2:类比点与圆的位置关系的判断,我们怎样判断直线与圆的位置关系?
方法一:几何法(根据圆心到直线的距离与圆半径的大小关系判断)
若圆心(a,b)到直线L的距离为d
(1)d < r ;
(2)d = r ;
(3)d > r .
方法二:代数法(根据直线与圆的公共点个数判断)
联立直线与圆的方程 得到关于x(或y)的方程
(1)△ > 0 ;
(2)△ = 0 ;
(3)△ < 0 .
知识应用
例1.如图1,已知直线和圆心为C的圆.判断直线 与圆的位置关系;如果相交,求出他们交点的坐标.
变式训练:判断直线L:与圆O:的位置关系.
例2.已知过点M(-3,-3)的直线被圆所截得的弦长为,求
的方程。
变式训练:直线y = 2x + b与圆相交于A、B两点,则弦AB的中点M的轨迹方程是 。
例4.已知点是圆上一点,求过点P的圆C的切线方程。
巩固练习
1.直线4x – 3y = 0和圆 x2 + y2 – 18x – 45 = 0的位置关系是 ( )
A.相交 B.相离 C.相切 D.不确定.
2.直线 与圆x2 + y2 - 2 x - 2 = 0相切,则实数m等于 ( )
A.或 B.或 C.或 D.或
3.直线l: x - y + 4 = 0圆C: (x-1)2 + (y - 1)2 = 2,则C上各点到l距离最小值为( )
A. B. C.3 D.
4.已知圆方程,直线,当为何值时,圆与直线相交、相切、相离.
5.过点P(1,-1)的直线l与圆M:
(1)当直线和圆相切时,求切线方程和切线长;
(2)若直线的斜率为2,求直线被圆截得的弦AB的长;
(3)若圆的方程加上条件x≥3,直线与圆有且只有一个交点,求直线的斜率的取值范围.
