苏教版高中数学平面向量(文科)一轮复习材料
文档属性
| 名称 | 苏教版高中数学平面向量(文科)一轮复习材料 |

|
|
| 格式 | rar | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-06-23 00:00:00 | ||
图片预览










文档简介
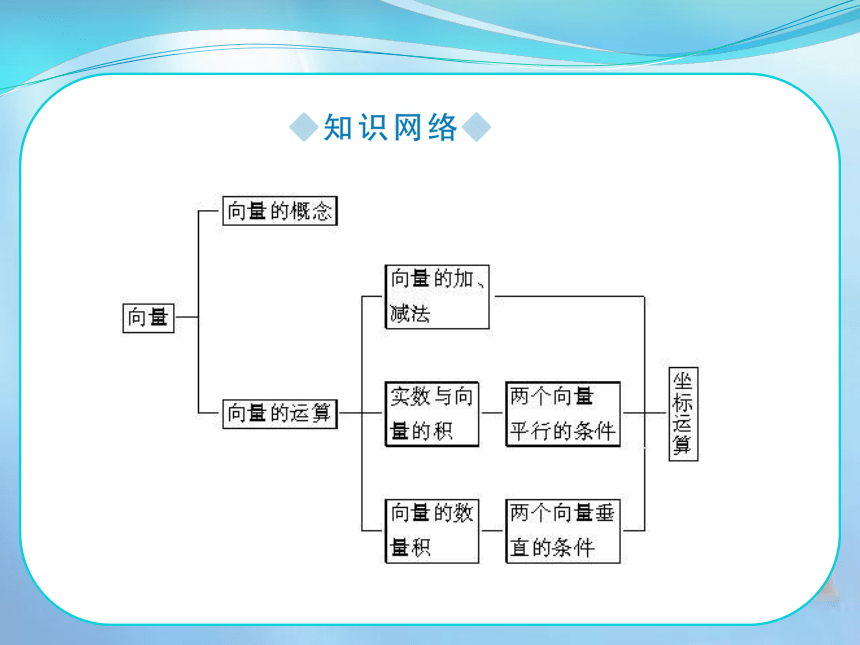
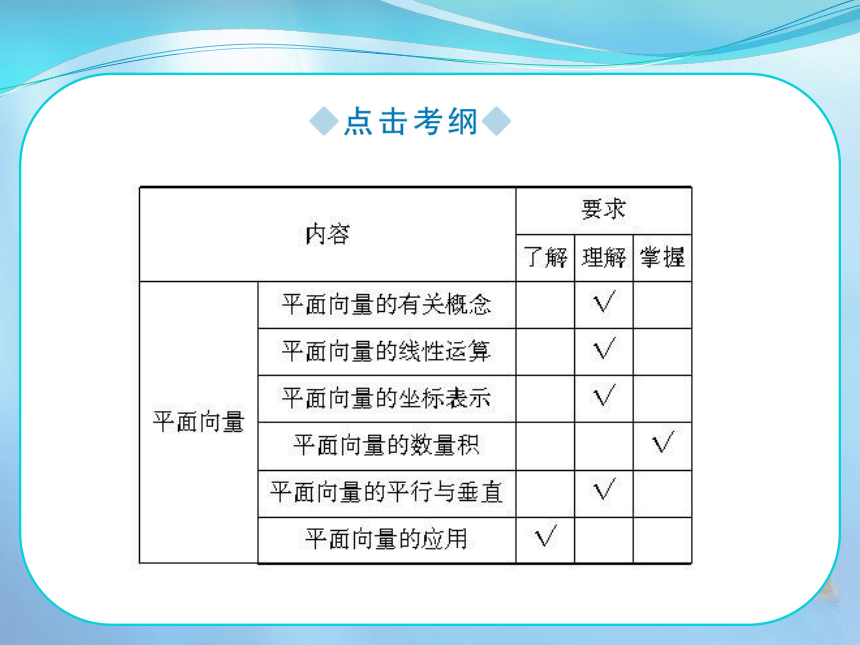
课件69张PPT。 向量是数学中的重要概念,它广泛应用于生产实践和科学研究中,其重要性逐渐加强,它是高中数学中的工具性知识,在高考中占有较大的比重.从近几年高考试题可以看出,主要考查平面向量的加减运算、平面向量的坐标表示、平面向量的数量积等基本概念、运算及简单应用. 在向量与平面几何、解析几何、三角等内容的交汇点处命题,综合性强,难度比较大,“平面向量”已成为命题的热点.对于向量的加法、减法运算既要注重几何运算,又要注重代数运算.另外要注意强化数学思想的学习,如数形结合思想、化归思想等.尤其是向量的坐标运算体现了数与形互相转化和密切结合的思想,所以要通过向量法和坐标法的运用,进一步体会数形结合思想在解决数学问题上的作用.1.平面向量的有关概念
(1)向量的定义:既有 又有方向的量叫做向量.
(2)表示方法:用 来表示向量,有向线段的 表示向量的大小,
用 所指的方向表示向量的方向,用字母a,b,…或用AB,BC,…表示.
(3)模:向量的 叫向量的模,记作|a|或|AB|.
(4)零向量:长度为零的向量叫做零向量,记作0;零向量的 不确定.
(5)单位向量:长度为 的向量叫做单位向量.
(6)共线向量:方向 的向量叫共线向量,规定 与任何向量
共线.
(7)相等的向量:长度 且方向 的向量叫相等的向量.大小长度有向线段1个长度单位相同或相反零向量相等相同长度箭头方向2.向量的加法
(1)定义:求两个向量和的运算,叫做向量的加法.
(2)法则: 法则、 法则.
(3)运算律:a+b=b+a;(a+b)+c=a+(b+c).
3.向量的减法
(1)定义:求两个向量差的运算,叫做向量的减法.
(2)法则: 则、 法则.
4.实数与向量的积
(1)定义:实数λ与向量a的积是 ,记作λa,规定:|λa|=|λ||a|.当λ>0
时,λa的方向与a的方向相同;当λ<0时,λa的方向与a的方向 ;当λ=0
时,λa与a平行.
(2)运算律:λ(μa)=(λμ)a,(λ+μ)a=λa+μa,λ(a+b)=λa+λb.
(3)与a平行的单位向量e=±.三角形平行四边形三角形法平行四边形一个向量相反5.两个重要定理
(1)向量共线定理:向量b与非零向量a共线的充要条件是 一个实
数λ,使得 ,即b∥a? (a≠0).
(2)平面向量基本定理:如果e1、e2是同一平面内的两个不共线向量,那么
对于这一平面内的任一向量a,有且仅有一对实数λ1、λ2,使a=λ1e1+λ2e2.有且仅有1.如图3-1-1,在平行四边形ABCD中,下列结论中正确的有________.
图3-1-1【答案】 ①②④
b=λab=λa2.在△ABC中,AB=c,AC=b.若点D满足BC=3DC,则AD=________.
【解析】 ∵BC= AC-AB=b-c,
【答案】3.【解析】【答案】 AB
4.设e1,e2是两个不共线的向量,而e1-4e2和ke1+e2共线,则实数k的值为________.
【答案】
【解析】6.l1、l2是不共线向量,且a=-l1+3l2,b=4l1+2l2,c=-3l1+12l2,用b、c为基底来表示向量a.
【解】 设a=λ1b+λ2c,即-l1+3l2=λ1(4l1+2l2)+λ2(-3l1+12l2),
即-l1+3l2=(4λ1-3λ2)l1+(2λ1+12λ2)l2,代数运算
向量的代数运算同数量的运算不一样,运算律也有异同,其中加减运算同字母的加减运算类似.
若3m+2n=a,m-3n=b,其中a,b是已知向量,求m,n.
【点拨】 向量加减的代数运算,与字母的代数运算一样,可以加减消元、代入消元.
【解】 记3m+2n=a①
m-3n=b②
3×②得3m-9n=3b③
①-③得11n=a-3b 用共线向量求值点共线转化成向量共线,要进行向量化,利用向量共线定理,就能得出相应的关系.
设e1,e2是两个不共线向量,已知=2e1+ke2,=e1+3e2,=2e1-e2,若三点A,B,D共线,求k的值.
【点拨】 三点共线的证明
向量共线的充要条件常用来解决三点共线和两直线平行问题 【点拨】 证明充要条件要分两个方向的证明.
【证明】 【证明】 几何中的线性表示
数形结合思想是向量加法、减法运算的核心,向量是一个几何量,是有“形”
的量,因此在解决向量有关问题时,多数习题要结合图形进行分析判断求解,
这是研究平面向量最重要的方法与技巧.图3-1-2
【点拨】 用已知向量来表示另外一些向量是用向量解题的基本要领,
要尽可能地转化到平行四边形或三角形中去.
【解】图3-1-3【解】规律总结 解决向量的概念问题要注意两点:一是不仅要考虑向量的大小,更重要的是要考虑向量的方向;二是考虑零向量是否也满足条件.在利用向量减法时,易弄错两向量的顺序,从而求得所求向量的相反向量,导致错误.图3-1-4
【点拨】 向量的分解可利用平面向量基本定理,要注意尽可能地转化到平
行四边形或三角形中去.
【解析】 【误区警示】 本题不少学生找不到解题的思路,有的学生利用正、余弦定理运算量大,结果还是不正确.事实上,本题除了用上述解法外,还可以以A点
为原点,AB、AC为坐标轴建立坐标系,采用坐标法来解.
【命题趋势】 平面向量每年必考小题,在本节中主要考查向量运算的几何性质、向量共线条件,至于向量的基本定理的问题在高考中也出现过,但要求不是太高.学而时习之,不亦说乎?第二节 向量的坐标形式学生P401.已知a=(x1,y1),b=(x2,y2),则a+b=(x1+x2,y1+y2),a-b= ,已知a=(x,y)和实数λ,那么λa=__________
(x1-x2,y1-y2)(λx,λy).【答案】 (-1,-1)
2.设向量a=(1,-3),b=(-2,4),若表示向量4a、3b-2a,c的有向线段首尾相接能构成三角形,则向量c=________.
【解析】 4a=(4,-12),3b-2a=(-8,18),设向量c=(x,y),依题意,得4a+(3b-2a)+c=0,则4-8+x=0,-12+18+y=0,解得x=4,y=-6.
【答案】 (4,-6)3.若平面向量a,b,满足|a+b|=1,a+b平行于x轴,b=(2,-1),则a=________.
【解析】 a+b=(1,0)或(-1,0),
则a=(1,0)-(2,-1)=(-1,1)
或a=(-1,0)-(2,-1)=(-3,1).
【答案】 (-1,1)或(-3,1)【解析】【答案】 【解析】 ka-b=k(2,3)-(-1,2)=(2k+1,3k-2)
a-kb=(2,3)-k(-1,2)=(2+k,3-2k)
∴(2k+1)(3-2k)-(3k-2)(2+k)=0,
∴7k2=7,∴k=±1.
【答案】 ±1
6.平面内给定三个向量a=(3,2),b=(-1,2),c=(4,1).
求满足a=mb+nc的实数m与n.
【解】 由题意得(3,2)=m(-1,2)+n(4,1),
向量共线
平面向量的坐标表示实际上是向量的代数表示,它可以使向量运算完全代数化,把关于向量的代数运算与坐标运算联系起来.【点拨】【解】 设P的坐标为(x,y),
最值问题
向量中最值问题不少都转化为函数最值问题来解决,因此解题关键在于寻找变量,以构造函数.
【点拨】 本题可以设出的坐标,然后利用向量共线找出x与y的关系,代入数量积的结果,可以得出二次函数,本题就可以利用二次函数求最值.【解】 几何问题
向量的加、减法,实数与向量的积是向量的基本运算,对于用坐标表示的向量需运用向量的坐标运算法则,而几何图形中的向量应结合向量加、减法的几何意义以方便寻找关系.
(2)若△ABC为直角三角形,且∠A为直角,求实数m的值.【点拨】 点A、B、C能构成三角形,则说明三点不共线,即向量不共线,可以先求出共线的情况,然后利用补集思想,即可求出不共线的情况.
【解】 已知平面上三点的坐标分别为A(-2,1),B(-1,3),C(3,4),求点D的坐标使这四点构成平行四边形四个顶点.【解】
图3-2-1
共线的灵活运用 利用设参数求参数是解决向量问题的常用技巧,而方程(组)是求解工具,体现了向量坐标运算的优越性.
(本题满分14分)平面内给定三个向量a=(3,2),b=(-1,2),c=(4,1).回答下列问题:
(1)若(a+kc)∥(2b-a),求实数k;
(2)设d=(x,y)满足(d-c)∥(a+b)且|d-c|=1,求d.
【点拨】 (1)利用向量共线的充要条件,建立关于实数k的充要条件;(2)(d-c)∥(a+b)且|d-c|=1建立关于x、y的方程组.
【解】 (1)∵(a+kc)∥(2b-a),
又a+kc=(3+4k,2+k),2b-a=(-5,2),(2分)∴2×(3+4k)-(-5)×(2+k)=0,(4分)
规律总结
向量的坐标可以运算,点的坐标不能运算;引入平面向量的坐标使向量运算完全代数化,成了数与形结合的载体.许多几何问题,特别是共线、共点等较难问题,可以建立坐标系,设出点的坐标就可以转化为坐标运算来解决.(2009·重庆卷)已知向量a=(1,1),b=(2,x),若a+b与4b-2a平行,则实数x的值是________.
【点拨】 可以先求出向量a+b与4b-2a的坐标,然后利用“a∥b(b≠0)且设a=(x1,y1),b=(x2,y2)?x1y2-x2y1=0(x1,x2,y1,y2∈R)”求出x的值.
【解析】 解法一 因为a=(1,1),b=(2,x),
所以a+b=(3,x+1),4b-2a=(6,4x-2),
由于a+b与4b-2a平行,
得6(x+1)-3(4x-2)=0,解得x=2.解法二 因为a+b与4b-2a平行,
则存在常数λ,使a+b=λ(4b-2a),
即(2λ+1)a=(4λ-1)b,
根据向量共线的条件知,向量a与b共线,故x=2.
【误区警示】 结论“a∥b(b≠0)且a=(x1,y1),b=(x2,y2)?x1y2-x2y1=0”
与向量垂直中的数量积x1x2+y1y2=0有不少同学会混淆.实际上a=(x1,y1)
与b=(x2,y2)平行,对应坐标成比例,而为了避免分母为0的情况,即写成
积的形式,即:x1y2=x2y1.
【命题趋势】 本部分内容的考查主要是以填空题的形式出现,重点考查向
量的加法、减法、数乘运算,以及向量共线的坐标运算.有时也会出现在解
答题中,但仅会起到桥梁作用,穿插在平面几何、解析几何、三角等内容中.学而时习之,不亦说乎?第三节 向量的数量积(2)数量积的定义:已知两个非零向量a和b,它们的夹角为θ,则数量|a||b|cos θ叫做a与b的数量积,记作a·b,即a·b=|a||b|cos θ.
(3)数量积的几何意义:数量积a·b等于a的模与b在a方向上的投影|b|cos θ的乘积.
2.数量积的性质
(1)当a与b同向时,a·b=|a||b|;当a与b反向时,a·b=-|a||b|.【答案】 3【答案】 4.已知a、b均为单位向量,它们的夹角为60°,那么|a+3b|=________.
【解析】【答案】5.已知a=(-3,2),b=(-1,0),向量λa+b与a-2b垂直,则实数λ的值为________.
【解析】 向量λa+b=(-3λ-1,2λ),a-2b=(-1,2),因为两个向量垂直,故有(-3λ-1,2λ)·(-1,2)=0,即3λ+1+4λ=0,解得:λ=-.【答案】 【解】 模与夹角
平面向量的数量积可以考查数量积的运算,模与夹角等问题.对于模与夹角的问题,结合向量的数量积的定义,常利用平方法来处理.
设n和m是两个单位向量,其夹角是60°,求向量a=2m+n与b=2n-3m的夹角.
【点拨】 先利用已知条件求出向量n和m的数量积,然后再求向量a=2m+n与b=2n-3m的数量积,以及它们的模,即可求出向量a=2m+n与b=2n-3m的夹角.
【解】 垂直问题
利用向量的数量积处理垂直问题,都是利用向量的数量积为0,若有坐标,即利用x1x2+y1y2=0,就可以解决问题.
【点拨】 △ABC是直角三角形,但不知道谁是直角,因此需要分成三种情况进行分类讨论.
【解】 最值问题
在涉及向量数量积的最值问题中,往往是通过数量积的运算,利用函数或基本不等式来求最值.
【点拨】 本题要注意|a|=|b|=1,因此不要先求ka+b与a-kb的坐标,而是采用平方法,这样可以简化运算过程.
【解】已知a、b是两个非零向量,当a+tb(t∈R)的模取最小值时,
(1)求t的值;
(2)求证:b⊥(a+tb).
(1)【解】 设a与b的夹角为θ,则
|a+tb|2=(a+tb)2=|a|2+t2|b|2+2a·(tb)
=|a|2+t2|b|2+2t|a||b|cos θ
(2)【证明】 不等式问题
两向量的夹角为钝角,则它们的数量积小于0,但两向量的数量积小于0,不能说明它们的夹角为钝角.
(本题满分14分)设两向量e1、e2满足|e1|=2,|e2|=1,e1、e2的夹角为60°,若向量2te1+7e2与向量e1+te2的夹角为钝角,求实数t的取值范围.
【点拨】 向量2te1+7e2与向量e1+te2的夹角为钝角时,(2te1+7e2)·(e1+te2)<0.而(2te1+7e2)·(e1+te2)<0包含了两个向量反向共线的情况,因此要把反向共线时t的范围去掉.
【解】已知m∈R,a=(m-2,m+3),b=(2m+1,m-2),向量a,b的夹角为钝角,求实数m的取值范围.
【解】 ∵a·b=(m-2)(2m+1)+(m-2)(m+3)=3m2-2m-8,
而向量a,b的夹角为钝角
规律总结
? 向量的数量积不满足结合律、消去律,即(a·b)·c≠a·(b·c),a·c=b·c不能推出a=b.可以用向量的数量积公式解决有关夹角和垂直问题,但要注意两种公式的灵活运用.利用向量垂直的充要条件研究几何中线线垂直的问题,常常建立适当的坐标系,得到简单的向量坐标表示,减少运算量.
(2009·安徽卷)给定两个长度为1的平面向量和,它们的夹角为120°.如图3-3-1所示,
图3-3-1
【点拨】 本题可以引进角参数,设∠AOC=α,然后利用向量的数量积列出关于参数的方程组.本题也可以以O为原点,OA为x轴建立坐标系,引入坐标运算.
【解析】 解法一 设∠AOC=α
【误区警示】 本题不少学生不知道灵活运用向量的数量积来做,或者想不到建立坐标系利用坐标来处理.本题不仅考查了向量的有关知识,而且还需要掌握三角函数的有关运算.
【命题趋势】 高考中多以填空题的形式考查向量数量积的运算,难度属于中、低档,向量的数量积也常用来判断三角形的形状、求两直线的夹角或线段的长度,以及最值等问题,易与其它知识结合,在知识交汇点处命题,一直是高考的热点.
学而时习之,不亦说乎?学而时习之,不亦说乎?
(1)向量的定义:既有 又有方向的量叫做向量.
(2)表示方法:用 来表示向量,有向线段的 表示向量的大小,
用 所指的方向表示向量的方向,用字母a,b,…或用AB,BC,…表示.
(3)模:向量的 叫向量的模,记作|a|或|AB|.
(4)零向量:长度为零的向量叫做零向量,记作0;零向量的 不确定.
(5)单位向量:长度为 的向量叫做单位向量.
(6)共线向量:方向 的向量叫共线向量,规定 与任何向量
共线.
(7)相等的向量:长度 且方向 的向量叫相等的向量.大小长度有向线段1个长度单位相同或相反零向量相等相同长度箭头方向2.向量的加法
(1)定义:求两个向量和的运算,叫做向量的加法.
(2)法则: 法则、 法则.
(3)运算律:a+b=b+a;(a+b)+c=a+(b+c).
3.向量的减法
(1)定义:求两个向量差的运算,叫做向量的减法.
(2)法则: 则、 法则.
4.实数与向量的积
(1)定义:实数λ与向量a的积是 ,记作λa,规定:|λa|=|λ||a|.当λ>0
时,λa的方向与a的方向相同;当λ<0时,λa的方向与a的方向 ;当λ=0
时,λa与a平行.
(2)运算律:λ(μa)=(λμ)a,(λ+μ)a=λa+μa,λ(a+b)=λa+λb.
(3)与a平行的单位向量e=±.三角形平行四边形三角形法平行四边形一个向量相反5.两个重要定理
(1)向量共线定理:向量b与非零向量a共线的充要条件是 一个实
数λ,使得 ,即b∥a? (a≠0).
(2)平面向量基本定理:如果e1、e2是同一平面内的两个不共线向量,那么
对于这一平面内的任一向量a,有且仅有一对实数λ1、λ2,使a=λ1e1+λ2e2.有且仅有1.如图3-1-1,在平行四边形ABCD中,下列结论中正确的有________.
图3-1-1【答案】 ①②④
b=λab=λa2.在△ABC中,AB=c,AC=b.若点D满足BC=3DC,则AD=________.
【解析】 ∵BC= AC-AB=b-c,
【答案】3.【解析】【答案】 AB
4.设e1,e2是两个不共线的向量,而e1-4e2和ke1+e2共线,则实数k的值为________.
【答案】
【解析】6.l1、l2是不共线向量,且a=-l1+3l2,b=4l1+2l2,c=-3l1+12l2,用b、c为基底来表示向量a.
【解】 设a=λ1b+λ2c,即-l1+3l2=λ1(4l1+2l2)+λ2(-3l1+12l2),
即-l1+3l2=(4λ1-3λ2)l1+(2λ1+12λ2)l2,代数运算
向量的代数运算同数量的运算不一样,运算律也有异同,其中加减运算同字母的加减运算类似.
若3m+2n=a,m-3n=b,其中a,b是已知向量,求m,n.
【点拨】 向量加减的代数运算,与字母的代数运算一样,可以加减消元、代入消元.
【解】 记3m+2n=a①
m-3n=b②
3×②得3m-9n=3b③
①-③得11n=a-3b 用共线向量求值点共线转化成向量共线,要进行向量化,利用向量共线定理,就能得出相应的关系.
设e1,e2是两个不共线向量,已知=2e1+ke2,=e1+3e2,=2e1-e2,若三点A,B,D共线,求k的值.
【点拨】 三点共线的证明
向量共线的充要条件常用来解决三点共线和两直线平行问题 【点拨】 证明充要条件要分两个方向的证明.
【证明】 【证明】 几何中的线性表示
数形结合思想是向量加法、减法运算的核心,向量是一个几何量,是有“形”
的量,因此在解决向量有关问题时,多数习题要结合图形进行分析判断求解,
这是研究平面向量最重要的方法与技巧.图3-1-2
【点拨】 用已知向量来表示另外一些向量是用向量解题的基本要领,
要尽可能地转化到平行四边形或三角形中去.
【解】图3-1-3【解】规律总结 解决向量的概念问题要注意两点:一是不仅要考虑向量的大小,更重要的是要考虑向量的方向;二是考虑零向量是否也满足条件.在利用向量减法时,易弄错两向量的顺序,从而求得所求向量的相反向量,导致错误.图3-1-4
【点拨】 向量的分解可利用平面向量基本定理,要注意尽可能地转化到平
行四边形或三角形中去.
【解析】 【误区警示】 本题不少学生找不到解题的思路,有的学生利用正、余弦定理运算量大,结果还是不正确.事实上,本题除了用上述解法外,还可以以A点
为原点,AB、AC为坐标轴建立坐标系,采用坐标法来解.
【命题趋势】 平面向量每年必考小题,在本节中主要考查向量运算的几何性质、向量共线条件,至于向量的基本定理的问题在高考中也出现过,但要求不是太高.学而时习之,不亦说乎?第二节 向量的坐标形式学生P401.已知a=(x1,y1),b=(x2,y2),则a+b=(x1+x2,y1+y2),a-b= ,已知a=(x,y)和实数λ,那么λa=__________
(x1-x2,y1-y2)(λx,λy).【答案】 (-1,-1)
2.设向量a=(1,-3),b=(-2,4),若表示向量4a、3b-2a,c的有向线段首尾相接能构成三角形,则向量c=________.
【解析】 4a=(4,-12),3b-2a=(-8,18),设向量c=(x,y),依题意,得4a+(3b-2a)+c=0,则4-8+x=0,-12+18+y=0,解得x=4,y=-6.
【答案】 (4,-6)3.若平面向量a,b,满足|a+b|=1,a+b平行于x轴,b=(2,-1),则a=________.
【解析】 a+b=(1,0)或(-1,0),
则a=(1,0)-(2,-1)=(-1,1)
或a=(-1,0)-(2,-1)=(-3,1).
【答案】 (-1,1)或(-3,1)【解析】【答案】 【解析】 ka-b=k(2,3)-(-1,2)=(2k+1,3k-2)
a-kb=(2,3)-k(-1,2)=(2+k,3-2k)
∴(2k+1)(3-2k)-(3k-2)(2+k)=0,
∴7k2=7,∴k=±1.
【答案】 ±1
6.平面内给定三个向量a=(3,2),b=(-1,2),c=(4,1).
求满足a=mb+nc的实数m与n.
【解】 由题意得(3,2)=m(-1,2)+n(4,1),
向量共线
平面向量的坐标表示实际上是向量的代数表示,它可以使向量运算完全代数化,把关于向量的代数运算与坐标运算联系起来.【点拨】【解】 设P的坐标为(x,y),
最值问题
向量中最值问题不少都转化为函数最值问题来解决,因此解题关键在于寻找变量,以构造函数.
【点拨】 本题可以设出的坐标,然后利用向量共线找出x与y的关系,代入数量积的结果,可以得出二次函数,本题就可以利用二次函数求最值.【解】 几何问题
向量的加、减法,实数与向量的积是向量的基本运算,对于用坐标表示的向量需运用向量的坐标运算法则,而几何图形中的向量应结合向量加、减法的几何意义以方便寻找关系.
(2)若△ABC为直角三角形,且∠A为直角,求实数m的值.【点拨】 点A、B、C能构成三角形,则说明三点不共线,即向量不共线,可以先求出共线的情况,然后利用补集思想,即可求出不共线的情况.
【解】 已知平面上三点的坐标分别为A(-2,1),B(-1,3),C(3,4),求点D的坐标使这四点构成平行四边形四个顶点.【解】
图3-2-1
共线的灵活运用 利用设参数求参数是解决向量问题的常用技巧,而方程(组)是求解工具,体现了向量坐标运算的优越性.
(本题满分14分)平面内给定三个向量a=(3,2),b=(-1,2),c=(4,1).回答下列问题:
(1)若(a+kc)∥(2b-a),求实数k;
(2)设d=(x,y)满足(d-c)∥(a+b)且|d-c|=1,求d.
【点拨】 (1)利用向量共线的充要条件,建立关于实数k的充要条件;(2)(d-c)∥(a+b)且|d-c|=1建立关于x、y的方程组.
【解】 (1)∵(a+kc)∥(2b-a),
又a+kc=(3+4k,2+k),2b-a=(-5,2),(2分)∴2×(3+4k)-(-5)×(2+k)=0,(4分)
规律总结
向量的坐标可以运算,点的坐标不能运算;引入平面向量的坐标使向量运算完全代数化,成了数与形结合的载体.许多几何问题,特别是共线、共点等较难问题,可以建立坐标系,设出点的坐标就可以转化为坐标运算来解决.(2009·重庆卷)已知向量a=(1,1),b=(2,x),若a+b与4b-2a平行,则实数x的值是________.
【点拨】 可以先求出向量a+b与4b-2a的坐标,然后利用“a∥b(b≠0)且设a=(x1,y1),b=(x2,y2)?x1y2-x2y1=0(x1,x2,y1,y2∈R)”求出x的值.
【解析】 解法一 因为a=(1,1),b=(2,x),
所以a+b=(3,x+1),4b-2a=(6,4x-2),
由于a+b与4b-2a平行,
得6(x+1)-3(4x-2)=0,解得x=2.解法二 因为a+b与4b-2a平行,
则存在常数λ,使a+b=λ(4b-2a),
即(2λ+1)a=(4λ-1)b,
根据向量共线的条件知,向量a与b共线,故x=2.
【误区警示】 结论“a∥b(b≠0)且a=(x1,y1),b=(x2,y2)?x1y2-x2y1=0”
与向量垂直中的数量积x1x2+y1y2=0有不少同学会混淆.实际上a=(x1,y1)
与b=(x2,y2)平行,对应坐标成比例,而为了避免分母为0的情况,即写成
积的形式,即:x1y2=x2y1.
【命题趋势】 本部分内容的考查主要是以填空题的形式出现,重点考查向
量的加法、减法、数乘运算,以及向量共线的坐标运算.有时也会出现在解
答题中,但仅会起到桥梁作用,穿插在平面几何、解析几何、三角等内容中.学而时习之,不亦说乎?第三节 向量的数量积(2)数量积的定义:已知两个非零向量a和b,它们的夹角为θ,则数量|a||b|cos θ叫做a与b的数量积,记作a·b,即a·b=|a||b|cos θ.
(3)数量积的几何意义:数量积a·b等于a的模与b在a方向上的投影|b|cos θ的乘积.
2.数量积的性质
(1)当a与b同向时,a·b=|a||b|;当a与b反向时,a·b=-|a||b|.【答案】 3【答案】 4.已知a、b均为单位向量,它们的夹角为60°,那么|a+3b|=________.
【解析】【答案】5.已知a=(-3,2),b=(-1,0),向量λa+b与a-2b垂直,则实数λ的值为________.
【解析】 向量λa+b=(-3λ-1,2λ),a-2b=(-1,2),因为两个向量垂直,故有(-3λ-1,2λ)·(-1,2)=0,即3λ+1+4λ=0,解得:λ=-.【答案】 【解】 模与夹角
平面向量的数量积可以考查数量积的运算,模与夹角等问题.对于模与夹角的问题,结合向量的数量积的定义,常利用平方法来处理.
设n和m是两个单位向量,其夹角是60°,求向量a=2m+n与b=2n-3m的夹角.
【点拨】 先利用已知条件求出向量n和m的数量积,然后再求向量a=2m+n与b=2n-3m的数量积,以及它们的模,即可求出向量a=2m+n与b=2n-3m的夹角.
【解】 垂直问题
利用向量的数量积处理垂直问题,都是利用向量的数量积为0,若有坐标,即利用x1x2+y1y2=0,就可以解决问题.
【点拨】 △ABC是直角三角形,但不知道谁是直角,因此需要分成三种情况进行分类讨论.
【解】 最值问题
在涉及向量数量积的最值问题中,往往是通过数量积的运算,利用函数或基本不等式来求最值.
【点拨】 本题要注意|a|=|b|=1,因此不要先求ka+b与a-kb的坐标,而是采用平方法,这样可以简化运算过程.
【解】已知a、b是两个非零向量,当a+tb(t∈R)的模取最小值时,
(1)求t的值;
(2)求证:b⊥(a+tb).
(1)【解】 设a与b的夹角为θ,则
|a+tb|2=(a+tb)2=|a|2+t2|b|2+2a·(tb)
=|a|2+t2|b|2+2t|a||b|cos θ
(2)【证明】 不等式问题
两向量的夹角为钝角,则它们的数量积小于0,但两向量的数量积小于0,不能说明它们的夹角为钝角.
(本题满分14分)设两向量e1、e2满足|e1|=2,|e2|=1,e1、e2的夹角为60°,若向量2te1+7e2与向量e1+te2的夹角为钝角,求实数t的取值范围.
【点拨】 向量2te1+7e2与向量e1+te2的夹角为钝角时,(2te1+7e2)·(e1+te2)<0.而(2te1+7e2)·(e1+te2)<0包含了两个向量反向共线的情况,因此要把反向共线时t的范围去掉.
【解】已知m∈R,a=(m-2,m+3),b=(2m+1,m-2),向量a,b的夹角为钝角,求实数m的取值范围.
【解】 ∵a·b=(m-2)(2m+1)+(m-2)(m+3)=3m2-2m-8,
而向量a,b的夹角为钝角
规律总结
? 向量的数量积不满足结合律、消去律,即(a·b)·c≠a·(b·c),a·c=b·c不能推出a=b.可以用向量的数量积公式解决有关夹角和垂直问题,但要注意两种公式的灵活运用.利用向量垂直的充要条件研究几何中线线垂直的问题,常常建立适当的坐标系,得到简单的向量坐标表示,减少运算量.
(2009·安徽卷)给定两个长度为1的平面向量和,它们的夹角为120°.如图3-3-1所示,
图3-3-1
【点拨】 本题可以引进角参数,设∠AOC=α,然后利用向量的数量积列出关于参数的方程组.本题也可以以O为原点,OA为x轴建立坐标系,引入坐标运算.
【解析】 解法一 设∠AOC=α
【误区警示】 本题不少学生不知道灵活运用向量的数量积来做,或者想不到建立坐标系利用坐标来处理.本题不仅考查了向量的有关知识,而且还需要掌握三角函数的有关运算.
【命题趋势】 高考中多以填空题的形式考查向量数量积的运算,难度属于中、低档,向量的数量积也常用来判断三角形的形状、求两直线的夹角或线段的长度,以及最值等问题,易与其它知识结合,在知识交汇点处命题,一直是高考的热点.
学而时习之,不亦说乎?学而时习之,不亦说乎?
