椭圆的几何性质

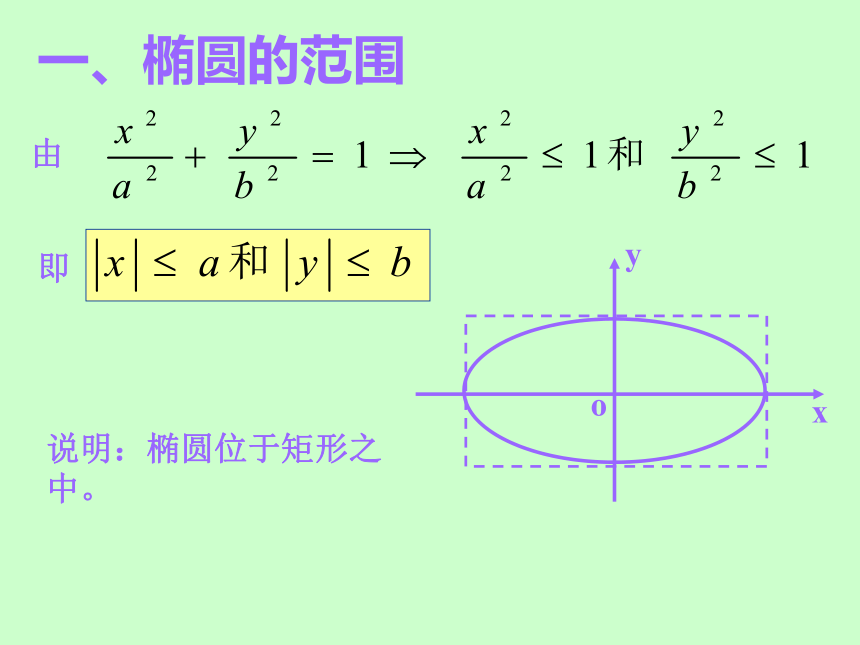
课件13张PPT。椭圆的几何性质一、椭圆的范围由即说明：椭圆位于矩形之中。二、椭圆的对称性在之中，把---换成---，方程不变，说明：
椭圆关于---轴对称；
椭圆关于---轴对称；
椭圆关于---点对称；
故，坐标轴是椭圆的对称轴，原点是椭圆的对称中心中心：椭圆的对称中心叫做椭圆的中心三、椭圆的顶点在中，令 x=0，得 y=？，说明椭圆与 y轴的交点？
令 y=0，得 x=？说明椭圆与 x轴的交点？*顶点：椭圆与它的对称轴的四个交点，叫做椭圆的顶点。
*长轴、短轴：线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。B1(0,b)B2(0,-b)A1(-a,0)A2(a,0)四、椭圆的离心率[1]离心率的取值范围：
因为 a > c > 0，所以1 >e >0[2]离心率对椭圆形状的影响：
1）e 越接近 1，c 就越接近 a，从而 b就越小（？），椭圆就越扁（？）
2）e 越接近 0，c 就越接近 0，从而 b就越大（？），椭圆就越圆（？）
3）特例：e =0，则 a = b，则 c=0，两个焦点重合，椭圆方程变为（？）
[2]上述方程表示的椭圆有几个对称轴？几个对称中心？[3]椭圆有几个顶点？顶点是谁与谁的交点？[4]对称轴与长轴、短轴是什么关系？[5]2a 和 2b是什么量？ a和 b是什么量？[6]关于离心率讲了几点？回 顾小结一：基本元素{1}基本量：a、b、c、e（共四个量）{2}基本点：顶点、焦点、中心（共七个点）{3}基本线：对称轴（共两条线）请考虑：基本量之间、基本点之间、基本线之间以及它们相互之间的关系（位置、数量之间的关系）例1 求椭圆 16 x2 + 25y2 =400的长轴和短轴的长、离心率、焦点和顶点坐标解：把已知方程化成标准方程这里，因此，椭圆的长轴长和短轴长分别是离心率焦点坐标分别是四个顶点坐标是例2 如图所示，我国发射的第一颗人造地球
卫星运行轨道是以地心(地球的中心)为一个焦点的椭圆，已知它的近地点A(离地
面最近的点)距地面555km，远地点B(离地面
最远的点)距地面74051km，并且 、A、B在同一直线上，设地球半径约为6371km，
求卫星运行的轨道方程 (精确到1km)．例3 有一椭圆形溜冰场,长轴长100m,短轴长60m.现要求在溜冰场上划定一个各顶点都在溜冰场边界上的矩形区域,且使这个矩形区域的面积最大,那么应把这个矩形的顶点定在何处?这时矩形的面积是多少?建立如图所示直角坐标系 1．P为 椭圆上的点，且P与焦点的连线互相垂直，求P2．椭圆 上不同三点
与焦点F(4,0)的距离成等差数列，求证3．设P是以0为中心的椭圆上任意一点， 为右焦点，求证：以线段 为直径的圆与此椭圆长轴为直径的圆内切设椭圆方程为