《简单的线性规划问题(1)》
图片预览







文档简介
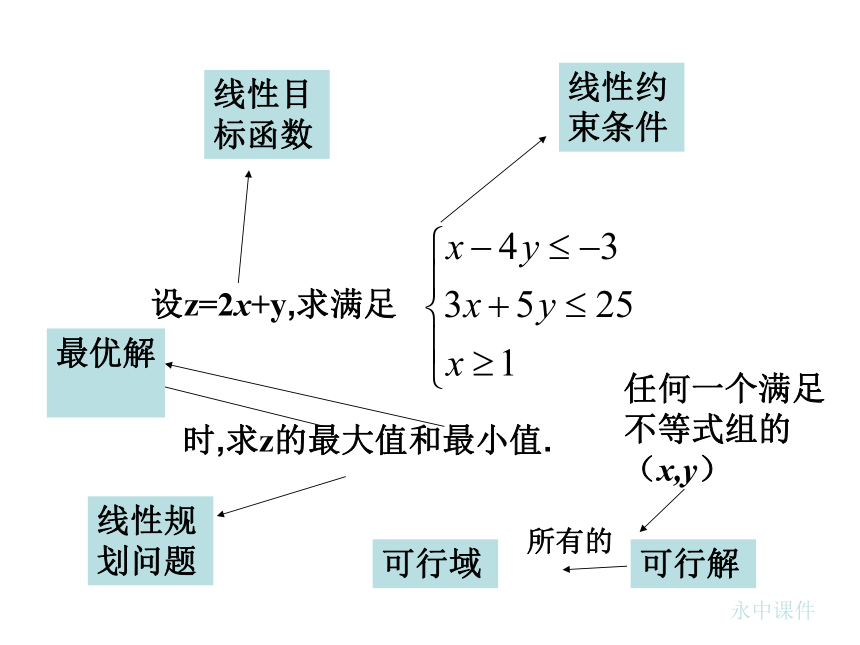
课件46张PPT。简单线性规划(1)江苏省常熟中学高一数学备课组表示的平面区域.作出不等式组复习:y有 关 概 念1 由x,y 的不等式(或方程)组成的不等式组称为
x,y 的约束条件;2 关于x,y 的一次不等式或方程组成的不等式
组称为x,y 的线性约束条件;欲达到最大值或最小值所涉及的变量x,y 的
解析式称为目标函数;4 关于x,y 的一次目标函数称为线性目标函数;使目标函数取得最大值或最小值的可行解称为
最优解.有 关 概 念5 求线性目标函数在线性约束条件下的最大
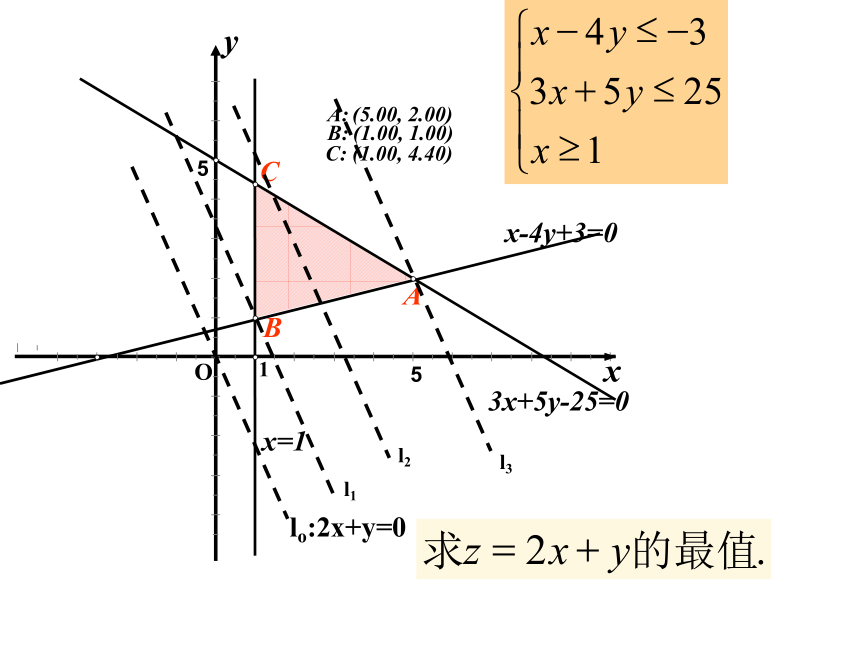
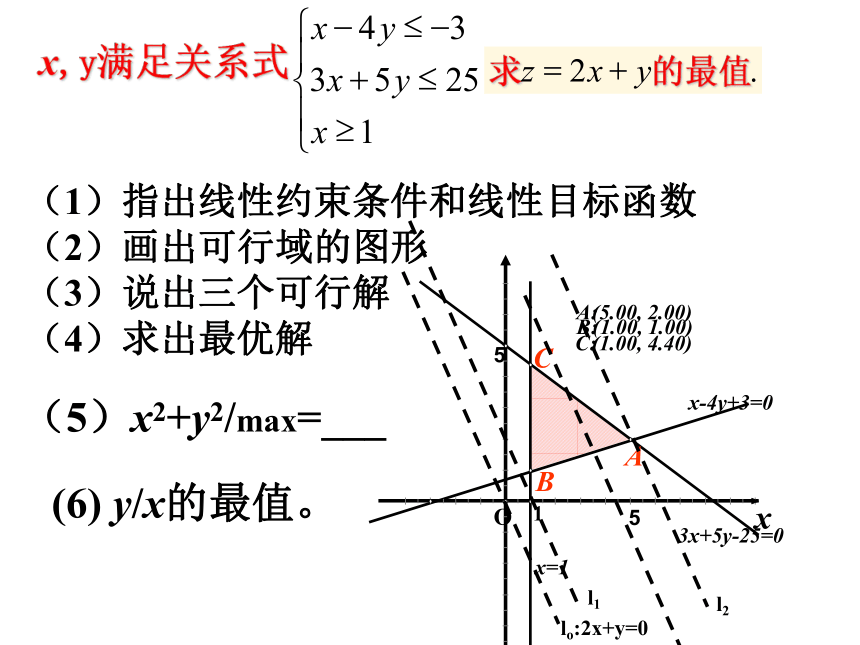
值或最小值问题称为线性规划问题;6 满足线性约束条件的解(x,y)称为可行解;7 所有可行解组成的集合称为可行域;线性目标函数线性约束条件线性规划问题任何一个满足不等式组的(x,y)可行解可行域所有的最优解永中课件(1)指出线性约束条件和线性目标函数
(2)画出可行域的图形
(3)说出三个可行解
(4)求出最优解(5)x2+y2/max=___(6) y/x的最值。解线性规划问题的步骤: (1)画:画出线性约束条件所表示的可行域; (2)移:在线性目标函数所表示的一组平行线中,
利用平移的方法找出与可行域有公共点
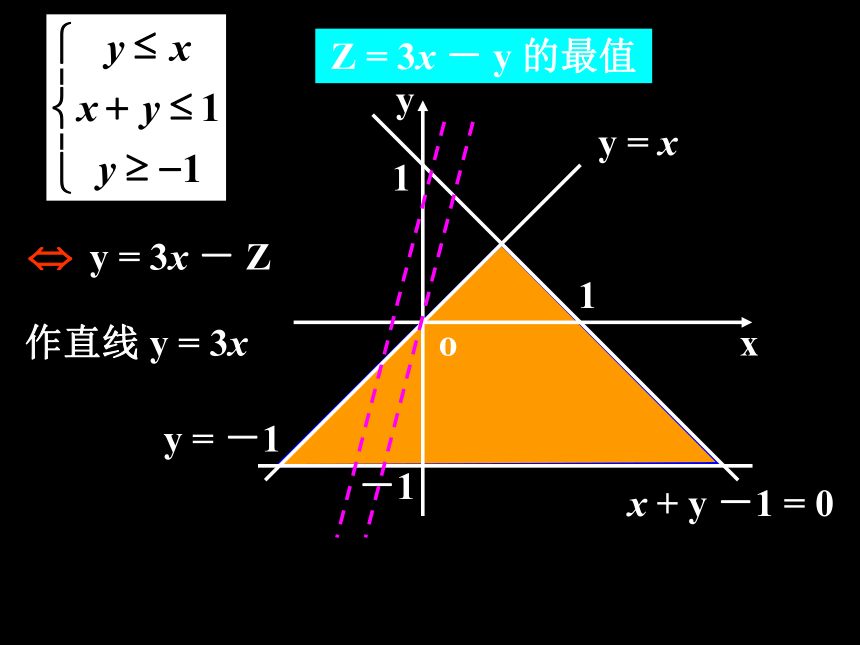
且纵截距最大或最小的直线; (3)求:通过解方程组求出最优解; (4)答:作出答案.解下列线性规划问题:1、求 Z = 3x -y 的最大值和最小值,使式中
的 x、y 满足约束条件
2、 图中阴影部分的点满足不等式组
在这些点中,使目标函数 k = 6x + 8y
取得最大值的点的坐标是__________Z = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ max = 7, Z min = -2Z = 3x - y 的最值y = 3x - Z作直线 y = 3xk = 6x + 8y
取最大值时的点作直线 y = x作直线 y = xk = 6x + 8y
取最大值时的点作直线 y = xk = 6x + 8y
取最大值时的点作直线 y = xk = 6x + 8y
取最大值时的点作直线 y = xk = 6x + 8y
取最大值时的点作直线 y = xk = 6x + 8y
取最大值时的点作直线 y = xk = 6x + 8y
取最大值时的点作直线 y = xk = 6x + 8y
取最大值时的点作直线 y = xk = 6x + 8y
取最大值时的点作直线 y = xk = 6x + 8y
取最大值时的点作直线 y = x由图知:最大值
的点为 ( 0 , 5 )k = 6x + 8y
取最大值时的点2、求线性目标函数的最优解,要注意分析
线性目标函数所表示的几何意义 ——在y轴上的截距或其相反数.几个结论:1、线性目标函数的最大(小)值一般在
可行域的顶点处取得,也可能在边界
处取得.3 、对于实际问题,要准确理解题意,能够把具体问题转化为线性规划的问题去解决.
x,y 的约束条件;2 关于x,y 的一次不等式或方程组成的不等式
组称为x,y 的线性约束条件;欲达到最大值或最小值所涉及的变量x,y 的
解析式称为目标函数;4 关于x,y 的一次目标函数称为线性目标函数;使目标函数取得最大值或最小值的可行解称为
最优解.有 关 概 念5 求线性目标函数在线性约束条件下的最大
值或最小值问题称为线性规划问题;6 满足线性约束条件的解(x,y)称为可行解;7 所有可行解组成的集合称为可行域;线性目标函数线性约束条件线性规划问题任何一个满足不等式组的(x,y)可行解可行域所有的最优解永中课件(1)指出线性约束条件和线性目标函数
(2)画出可行域的图形
(3)说出三个可行解
(4)求出最优解(5)x2+y2/max=___(6) y/x的最值。解线性规划问题的步骤: (1)画:画出线性约束条件所表示的可行域; (2)移:在线性目标函数所表示的一组平行线中,
利用平移的方法找出与可行域有公共点
且纵截距最大或最小的直线; (3)求:通过解方程组求出最优解; (4)答:作出答案.解下列线性规划问题:1、求 Z = 3x -y 的最大值和最小值,使式中
的 x、y 满足约束条件
2、 图中阴影部分的点满足不等式组
在这些点中,使目标函数 k = 6x + 8y
取得最大值的点的坐标是__________Z = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ = 3x - y 的最值y = 3x - Z作直线 y = 3xZ max = 7, Z min = -2Z = 3x - y 的最值y = 3x - Z作直线 y = 3xk = 6x + 8y
取最大值时的点作直线 y = x作直线 y = xk = 6x + 8y
取最大值时的点作直线 y = xk = 6x + 8y
取最大值时的点作直线 y = xk = 6x + 8y
取最大值时的点作直线 y = xk = 6x + 8y
取最大值时的点作直线 y = xk = 6x + 8y
取最大值时的点作直线 y = xk = 6x + 8y
取最大值时的点作直线 y = xk = 6x + 8y
取最大值时的点作直线 y = xk = 6x + 8y
取最大值时的点作直线 y = xk = 6x + 8y
取最大值时的点作直线 y = x由图知:最大值
的点为 ( 0 , 5 )k = 6x + 8y
取最大值时的点2、求线性目标函数的最优解,要注意分析
线性目标函数所表示的几何意义 ——在y轴上的截距或其相反数.几个结论:1、线性目标函数的最大(小)值一般在
可行域的顶点处取得,也可能在边界
处取得.3 、对于实际问题,要准确理解题意,能够把具体问题转化为线性规划的问题去解决.
