简单的线性规划问题(2)》
图片预览





文档简介
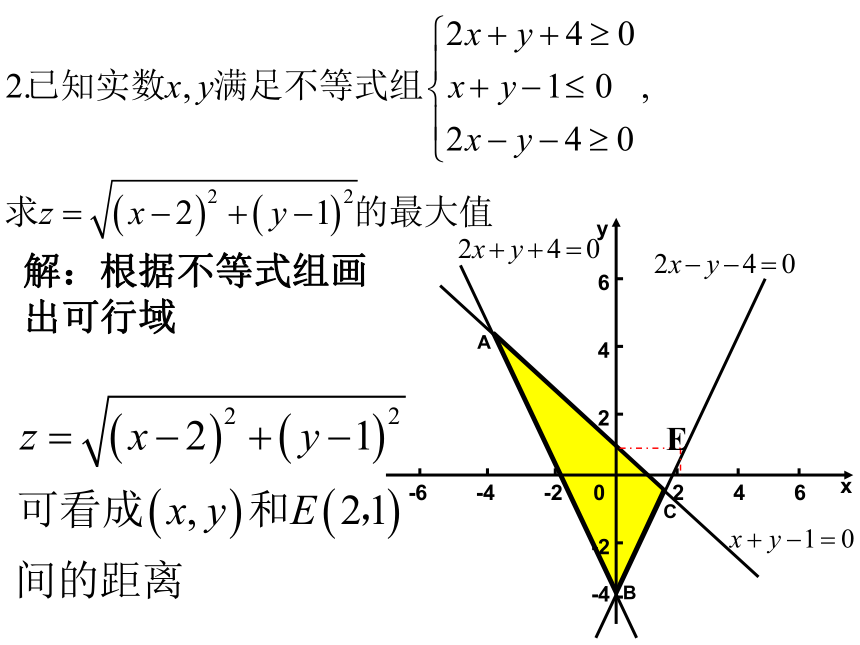
课件16张PPT。江苏省常熟中学高一数学备课组使z=2x+y取得最大值的可行解为 ,且最大值为 ;复习引入1.已知二元一次不等式组(1)画出平面区域;满足 的解(x,y)都叫
做可行解;z=2x+y 叫做 ;(2)设z=2x+y,则式中变量x,y满足的二元一次不等式组叫做x,y的 ;y=-1x-y=0x+y=12x+y=0(-1,-1) (2,-1)使z=2x+y取得最小值的可行解 ,
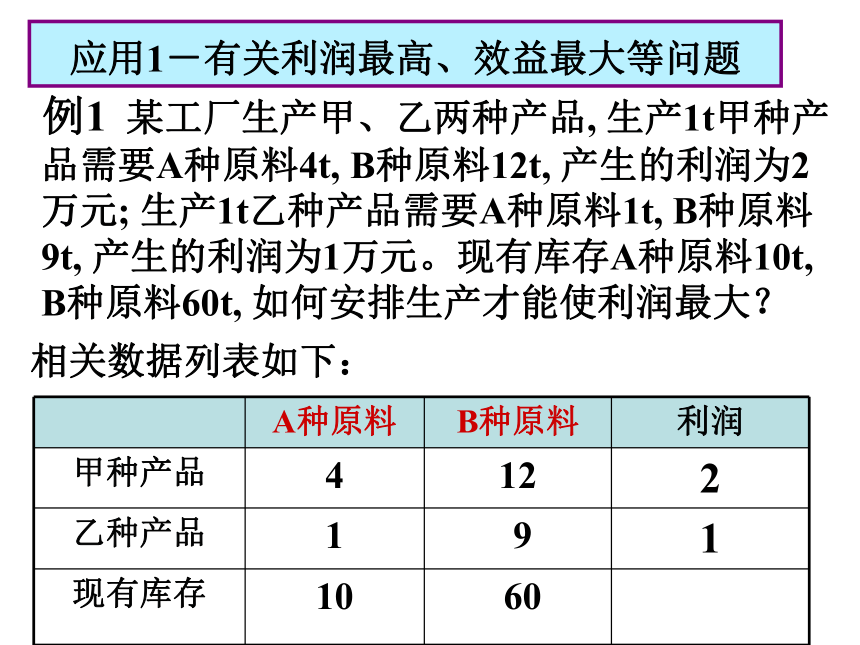
且最小值为 。线性约束条件线性目标函数线性约束条件(2,-1)(-1,-1)3-3解:根据不等式组画出可行域 例1 某工厂生产甲、乙两种产品, 生产1t甲种产品需要A种原料4t, B种原料12t, 产生的利润为2万元; 生产1t乙种产品需要A种原料1t, B种原料9t, 产生的利润为1万元。现有库存A种原料10t, B种原料60t, 如何安排生产才能使利润最大?相关数据列表如下:应用1-有关利润最高、效益最大等问题分析:设生产甲、乙两种产品的吨数
分别为x、y。则利润何时达到最大?解线性规划应用问题的一般步骤:2)设好变元并列出不等式组和目标函数 3)作出可行域;4)在可行域内求目标函数的最优解1)理清题意,列出表格:5)还原成实际问题法1:移-在线性目标函数所表示的一组平行线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线; 法2:算-线性目标函数的最大(小)值一般在可行域的顶点处取得,也可能在边界处取得(当两顶点的目标函数值相等时最优解落在一条边界线段上)。此法可弥补作图不准的局限。(画图力保准确) 某家具厂有方木料90m3,五合板600m3,准备加工成书桌和书橱,已知每张书桌要方木料0.1m3,五合板2m3,生产每个书橱要方木料0.2m3,五合板1m3,出售一张书桌可获利80元,出售一张书橱可获利120元,如果只安排生产书桌可获利多少,如果只安排生产书橱,可获利润多少?怎样安排生产可使所得利润最大???练习 由上表可知:(1)只生产书桌,用完五合板了,可生产书桌 600÷2=300张,可获利润:80×300=24000元,但木料没有用完 (2)只生产书橱,用完方木料,可生产书橱90÷0.2=450 张,可获利润120×450=54000元,但五合板没有用完可设生产书桌 x 张,书橱 y 张,最大利润为Z Z= 80 x + 120 yx∈Ny∈N300600A(100,400)1.某家具厂有方木材90m3,木工板600m3,准备加工成书桌和书橱出售,已知生产每张书桌需要方木料0.1m3、木工板2m3;生产每个书橱需要方木料0.2m3,木工板1m3,出售一张书桌可以获利80元,出售一张书橱可以获利120元;(1)怎样安排生产可以获利最大?(2)若只生产书桌可以获利多少?(3)若只生产书橱可以获利多少?(1)设生产书桌x张,书橱y张,利润为z元, 则约束条件为 Z=80x+120y作出不等式表示的平面区域,当生产100张书桌,400张书橱时利润最大为z=80×100+120×400=56000元(2)若只生产书桌可以生产300张,用完木工板,可获利 24000元;(3)若只生产书橱可以生产450张,用完方木料,可获利54000元。将直线z=80x+120y平移可知:900450求解:应用2-有关二元一次代数式取值范围解:由①、②同向相加可得: ③由②得 将上式与①同向相加得 ④③+④得以上解法正确吗?为什么?y?解:作线形约束条件所表示的平面区域,即如图所示四边形ABCD。作直线所以,求得 A(3,1) B(4,0)
C(5,1) D(4,2) 若实数x,y满足 求2x+y的取值范围练习: 已知:-1≤a+b≤1,1≤a-2b≤3
求: a+3b的取值范围。解: 约束条件为:目标函数为:z=a+3b由图形知:-11/3≤z≤1
即 -11/3≤a+3b≤1练习: 已知 f (x) = px2-q,
且 -4 ≤f (1) ≤ -1,-2 ≤f (2) ≤5求: f (3) 取 值 范 围
做可行解;z=2x+y 叫做 ;(2)设z=2x+y,则式中变量x,y满足的二元一次不等式组叫做x,y的 ;y=-1x-y=0x+y=12x+y=0(-1,-1) (2,-1)使z=2x+y取得最小值的可行解 ,
且最小值为 。线性约束条件线性目标函数线性约束条件(2,-1)(-1,-1)3-3解:根据不等式组画出可行域 例1 某工厂生产甲、乙两种产品, 生产1t甲种产品需要A种原料4t, B种原料12t, 产生的利润为2万元; 生产1t乙种产品需要A种原料1t, B种原料9t, 产生的利润为1万元。现有库存A种原料10t, B种原料60t, 如何安排生产才能使利润最大?相关数据列表如下:应用1-有关利润最高、效益最大等问题分析:设生产甲、乙两种产品的吨数
分别为x、y。则利润何时达到最大?解线性规划应用问题的一般步骤:2)设好变元并列出不等式组和目标函数 3)作出可行域;4)在可行域内求目标函数的最优解1)理清题意,列出表格:5)还原成实际问题法1:移-在线性目标函数所表示的一组平行线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线; 法2:算-线性目标函数的最大(小)值一般在可行域的顶点处取得,也可能在边界处取得(当两顶点的目标函数值相等时最优解落在一条边界线段上)。此法可弥补作图不准的局限。(画图力保准确) 某家具厂有方木料90m3,五合板600m3,准备加工成书桌和书橱,已知每张书桌要方木料0.1m3,五合板2m3,生产每个书橱要方木料0.2m3,五合板1m3,出售一张书桌可获利80元,出售一张书橱可获利120元,如果只安排生产书桌可获利多少,如果只安排生产书橱,可获利润多少?怎样安排生产可使所得利润最大???练习 由上表可知:(1)只生产书桌,用完五合板了,可生产书桌 600÷2=300张,可获利润:80×300=24000元,但木料没有用完 (2)只生产书橱,用完方木料,可生产书橱90÷0.2=450 张,可获利润120×450=54000元,但五合板没有用完可设生产书桌 x 张,书橱 y 张,最大利润为Z Z= 80 x + 120 yx∈Ny∈N300600A(100,400)1.某家具厂有方木材90m3,木工板600m3,准备加工成书桌和书橱出售,已知生产每张书桌需要方木料0.1m3、木工板2m3;生产每个书橱需要方木料0.2m3,木工板1m3,出售一张书桌可以获利80元,出售一张书橱可以获利120元;(1)怎样安排生产可以获利最大?(2)若只生产书桌可以获利多少?(3)若只生产书橱可以获利多少?(1)设生产书桌x张,书橱y张,利润为z元, 则约束条件为 Z=80x+120y作出不等式表示的平面区域,当生产100张书桌,400张书橱时利润最大为z=80×100+120×400=56000元(2)若只生产书桌可以生产300张,用完木工板,可获利 24000元;(3)若只生产书橱可以生产450张,用完方木料,可获利54000元。将直线z=80x+120y平移可知:900450求解:应用2-有关二元一次代数式取值范围解:由①、②同向相加可得: ③由②得 将上式与①同向相加得 ④③+④得以上解法正确吗?为什么?y?解:作线形约束条件所表示的平面区域,即如图所示四边形ABCD。作直线所以,求得 A(3,1) B(4,0)
C(5,1) D(4,2) 若实数x,y满足 求2x+y的取值范围练习: 已知:-1≤a+b≤1,1≤a-2b≤3
求: a+3b的取值范围。解: 约束条件为:目标函数为:z=a+3b由图形知:-11/3≤z≤1
即 -11/3≤a+3b≤1练习: 已知 f (x) = px2-q,
且 -4 ≤f (1) ≤ -1,-2 ≤f (2) ≤5求: f (3) 取 值 范 围
