《简单的线性规划问题(3)》
图片预览

文档简介
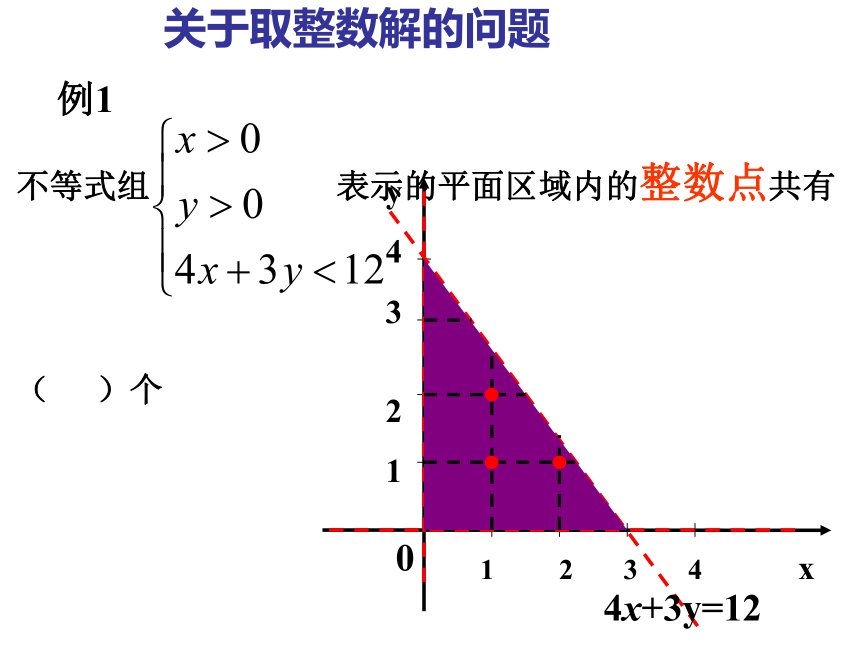
课件7张PPT。江苏省常熟中学高一数学备课组不等式组 表示的平面区域内的整数点共有 ( )个例1 1 2 3 4 xy
4
3
2
1
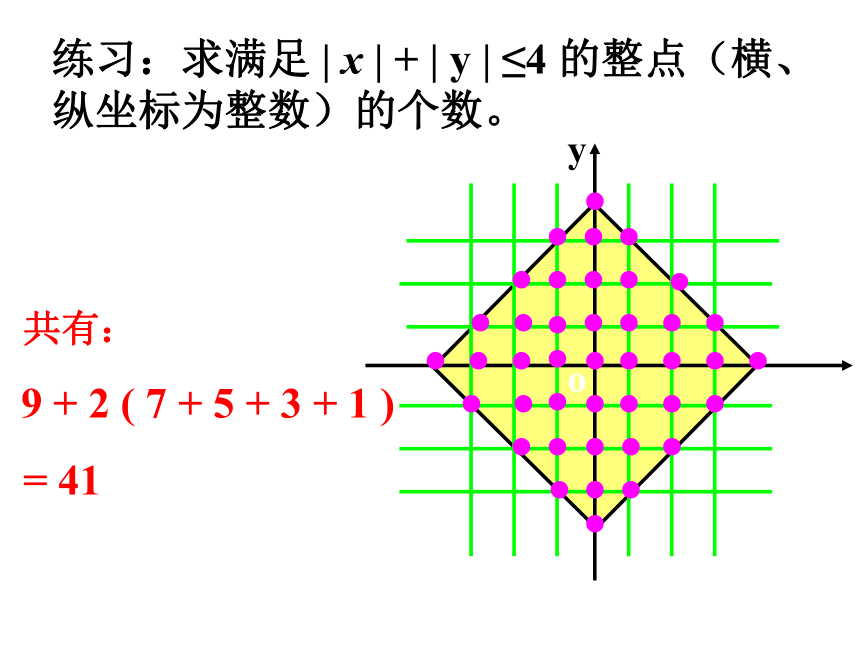
4x+3y=12关于取整数解的问题0练习:求满足 | x | + | y | ≤4 的整点(横、纵坐标为整数)的个数。共有:
9 + 2 ( 7 + 5 + 3 + 1 )
= 41 在可行域内找出最优解、线性规划整数解问题的一般方法是:1.若区域“顶点”处恰好为整点,那么它就是最优解;(在包括边界的情况下)2.在可行域内找整数解,一般采用平移
找解法,即打网络、找整点、平移直线、
找出整数最优解;还可以用调整最优值法。例2 某运输公司接受了向抗洪抢险地区每天至少运送180吨支援物资的任务,该公司有8辆载重量为6吨的A型卡车和4辆载重量为10吨的B型卡车,有10名驾驶员;每辆卡车每天往返的次数为A型卡车4次,B型卡车3次,每辆卡车每天往返的成本费A型卡车为320元,B型卡车为504元,问如何安排车辆才能使该公司所花的成本费最低,最低为多少元?(要求每型卡车至少安排一辆)4x=8y=4x+y=104x+5y=30320x+504y=0解:设每天调出的A型车x辆,B型车y辆,公司所花的费用为z元,则Z=320x+504y作出可行域中的整点,可行域中的整点(5, 2)使Z=320x+504y取得最小值,且Zmin=2608元作出可行域15课后练习:
4
3
2
1
4x+3y=12关于取整数解的问题0练习:求满足 | x | + | y | ≤4 的整点(横、纵坐标为整数)的个数。共有:
9 + 2 ( 7 + 5 + 3 + 1 )
= 41 在可行域内找出最优解、线性规划整数解问题的一般方法是:1.若区域“顶点”处恰好为整点,那么它就是最优解;(在包括边界的情况下)2.在可行域内找整数解,一般采用平移
找解法,即打网络、找整点、平移直线、
找出整数最优解;还可以用调整最优值法。例2 某运输公司接受了向抗洪抢险地区每天至少运送180吨支援物资的任务,该公司有8辆载重量为6吨的A型卡车和4辆载重量为10吨的B型卡车,有10名驾驶员;每辆卡车每天往返的次数为A型卡车4次,B型卡车3次,每辆卡车每天往返的成本费A型卡车为320元,B型卡车为504元,问如何安排车辆才能使该公司所花的成本费最低,最低为多少元?(要求每型卡车至少安排一辆)4x=8y=4x+y=104x+5y=30320x+504y=0解:设每天调出的A型车x辆,B型车y辆,公司所花的费用为z元,则Z=320x+504y作出可行域中的整点,可行域中的整点(5, 2)使Z=320x+504y取得最小值,且Zmin=2608元作出可行域15课后练习:
