《一元二次不等式2》课件(苏教版必修5)
文档属性
| 名称 | 《一元二次不等式2》课件(苏教版必修5) |

|
|
| 格式 | rar | ||
| 文件大小 | 753.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-06-24 00:00:00 | ||
图片预览






文档简介
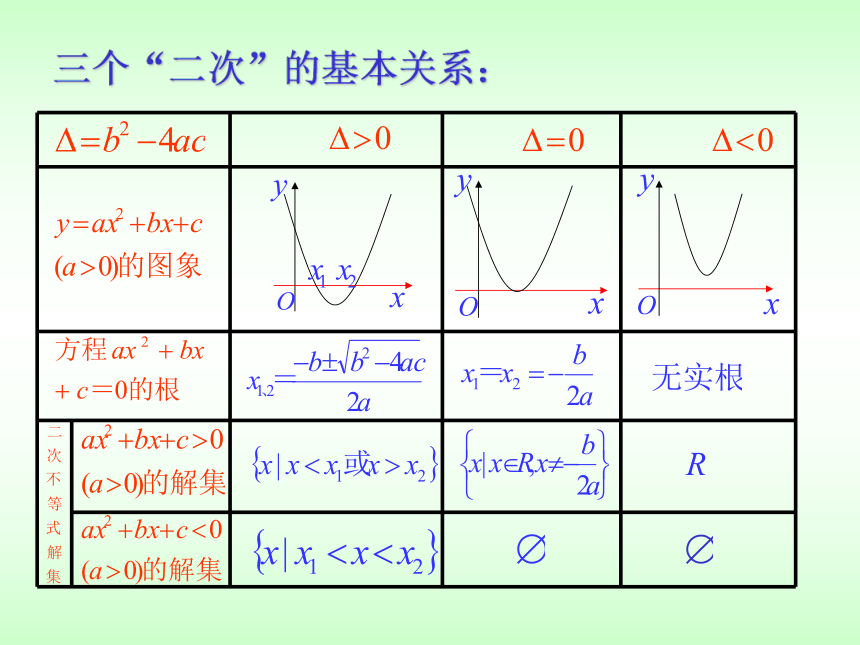
课件16张PPT。一元二次不等式第2课时2019年3月10日星期日修远中学 陈永和三个“二次”的基本关系:练习:解下列不等式.(1).(2).R(3).例1:解关于x的不等式x2-(a+1)x+a>0变形1:解关于x的不等式 x2-ax - (a+1) >0引申1:解关于x的不等式 ax2-(a+1)x+1>0 (a≠0) 变形2:求函数 的定义域。引申2:若 的定义域为R,求b范围。 拓展:若 的值域为R,求b范围。 注: 解形如ax2+bx+c>0的不等式时分类讨
论的标准有: 1、讨论a 与0的大小;2、讨论⊿与0的大小;3、讨论两根的大小;例5 关于x的二次不等式a2x2+6ax+9-b2 ≤ 0的解集是[-1,2],求a,b解:依题意知方程a2x2+6ax+9—b2=0
的两根为—1,2.∴ (1)二次不等式a x2 +bx +c > 0恒成立例题:已知关于x的不等式:(a-2)x2 + (a-2)x +1 ≥ 0恒成立, 解:由题意知: ①当a -2=0,即a =2时,不等式化为②当a -2≠0,即a ≠2时,原题等价于综上:试求a的取值范围.1 ≥ 0,它恒成立,满足条件.知识概要(2)二次不等式a x2 +bx +c < 0恒成立(3)二次不等式a x2 +bx +c ≥ 0恒成立(4)二次不等式a x2 +bx +c ≤ 0恒成立含参不等式恒成立的问题课堂小结方程函数不等式结合数形结合(二)两个结合(一)一般步骤:3.根据图象写出不等式的解集作业与思考R-12-2-2≤a≤6作业:73页 第1、2题解关于x的不等式x2 + 5ax + 6 > 0解:由题意,得:⊿=25a2-241.当⊿=25a2-24>0 ,2.当⊿=25a2-24=0 ,3.当⊿=25a2-24<0,解集为:解集为:解集为:R.备选题变式1. x2 + 5ax + 6a2 > 0 解:因式分解,得:(x+3a)(x+2a) > 0, 方程(x+3a)(x+2a) =0的两根为-3a、-2a. ①当-3a >-2a 即a <0时, 解集为:{x︱x>-3a 或 x<-2a}; ②当-3a =-2a 即a =0时, 解集为:{x︱x∈R且x≠0};
③当-3a <-2a 即a >0时,综上:当a >0时,解集为:{x︱x> -2a或x< -3a}.
当a =0时,解集为: {x︱x∈R且x≠0};当a <0时,解集为:{x︱x> -3a或x< -2a};
解集为:{x︱x> -2a 或 x< -3a}.原不等式为 x2>0变式2. ax2 + (6a+1)x + 6 > 0二、当a≠0时,①当a<0时,一、当a=0时, ②当a>0时,⑴⑶⑵∴综上,得
论的标准有: 1、讨论a 与0的大小;2、讨论⊿与0的大小;3、讨论两根的大小;例5 关于x的二次不等式a2x2+6ax+9-b2 ≤ 0的解集是[-1,2],求a,b解:依题意知方程a2x2+6ax+9—b2=0
的两根为—1,2.∴ (1)二次不等式a x2 +bx +c > 0恒成立例题:已知关于x的不等式:(a-2)x2 + (a-2)x +1 ≥ 0恒成立, 解:由题意知: ①当a -2=0,即a =2时,不等式化为②当a -2≠0,即a ≠2时,原题等价于综上:试求a的取值范围.1 ≥ 0,它恒成立,满足条件.知识概要(2)二次不等式a x2 +bx +c < 0恒成立(3)二次不等式a x2 +bx +c ≥ 0恒成立(4)二次不等式a x2 +bx +c ≤ 0恒成立含参不等式恒成立的问题课堂小结方程函数不等式结合数形结合(二)两个结合(一)一般步骤:3.根据图象写出不等式的解集作业与思考R-12-2-2≤a≤6作业:73页 第1、2题解关于x的不等式x2 + 5ax + 6 > 0解:由题意,得:⊿=25a2-241.当⊿=25a2-24>0 ,2.当⊿=25a2-24=0 ,3.当⊿=25a2-24<0,解集为:解集为:解集为:R.备选题变式1. x2 + 5ax + 6a2 > 0 解:因式分解,得:(x+3a)(x+2a) > 0, 方程(x+3a)(x+2a) =0的两根为-3a、-2a. ①当-3a >-2a 即a <0时, 解集为:{x︱x>-3a 或 x<-2a}; ②当-3a =-2a 即a =0时, 解集为:{x︱x∈R且x≠0};
③当-3a <-2a 即a >0时,综上:当a >0时,解集为:{x︱x> -2a或x< -3a}.
当a =0时,解集为: {x︱x∈R且x≠0};当a <0时,解集为:{x︱x> -3a或x< -2a};
解集为:{x︱x> -2a 或 x< -3a}.原不等式为 x2>0变式2. ax2 + (6a+1)x + 6 > 0二、当a≠0时,①当a<0时,一、当a=0时, ②当a>0时,⑴⑶⑵∴综上,得
